随机事件分析

2019/01/052257 浏览闲聊讨论

20190105

从1.5版本开始引入了野外随机事件，可以触发恶虎（老虎碎片，升阶石），恶熊（精金石），强盗大队（5元宝），叛军大队（10元宝），答题（10元宝，共20种题目），神秘商店（1.6版本引入）。除去每天两次神秘商店（间隔4小时），其它随机事件每天一共30次，其中答题固定为10次。笔者想对随机事件触发概率做个分析，然而每天坚持刷满30次随机事件还是蛮累的，故跨越了3个版本，近期终于刷够了30次的每天30次，根据百度百科，样本容量30以上可以算作大样本，以下应用大样本统计方法。

1.30次实验数据如图1所示，其中0表示小怪，1表示恶虎，2表示恶熊，3表示强盗大队，4表示叛军大队，5表示答题。可以看出每天刷怪次数（含随机事件）从最小204次到最大538次不等，平均为386.6次，从而可知随机事件发生概率很可能小于10%，属于小概率事件，且每次实验有成功30次的上限，应用二项分布统计不方便，故考虑用负二项分布来统计分析。

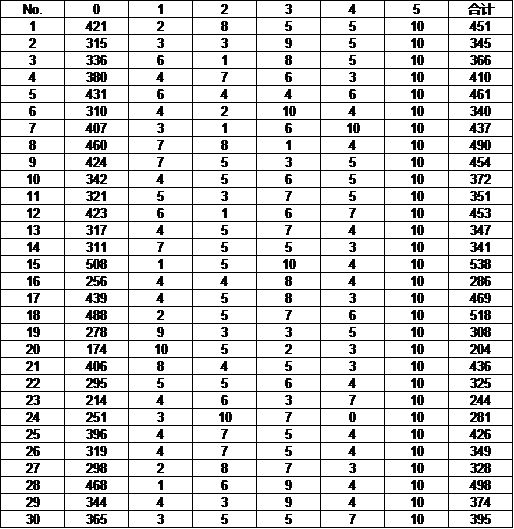
图1 实验数据

2.负二项分布的定义及其参数p的区间估计。图2是负二项分布的定义，此处按照发生随机事件为实验成功，概率记为p。图3是负二项分布在大样本情况下的区间估计，此处取显著性水平α=5%，即对p的区间估计置信度为95%。

图2 负二项分布的定义

图3 负二项分布未知参数p在大样本情况下的区间估计

根据图1所示数据以及图3公式，可以算出p的置信区间为(7.3%, 8.2%)，p的点估计为30/386.6=7.8%。根据图2所示负二项分布定义，以及上述区间估计，可以算出为了完成30次随机事件，以95%的概率会发生刷怪次数不超过509次，刷怪次数不少于236次。以上假定程序内置的简单随机模型，如果随机事件发生的概率不是固定的，例如与已发生随机事件次数有关，或与日期等其它机制有关，则不能按照以上理论分析，而需要更多的实验次数，来进行模型检验。

3.图4为20种答题的参考答案，供萌新参考。图5为实验原始数据，有兴趣的朋友可以据此进行初步模型检验，即验证p的稳定性。