几乎无法达成的团本极限--森林2525+理论分析
2022/10/012901 浏览玩家攻略
序言:
本帖子站在最客观的角度进行讲解,论事不论人,不喜勿喷
正文:
自从撰写了速度机制之后,几个精通团本森林的朋友来找我比较不同跑法的速度。我使用60帧的设备逐帧对比不同跑法的2523视频,将全图细节处理的最优解拼接到一起,得到了这样一个结论:2523不是极限!
在这个观点提出一个月后,琳琳就将其变为现实
自从琳琳打出了2524后,我便觉得森林的极限尘埃落定,就如同我上面图片说的那样,熊猫切流派可探索的点只剩下“完美的点地”了,再想通过改善细节而提高分数,这不太可能。
9月25日,我偶然刷到了老版本仓牙的2550跑法,便突发奇想:如果熊猫跑法复刻2550的路线,甚至更极限一点--不走传送门,直冲冲的飞到终点,这样会不会更快!我和好友oo以及芒果讨论了两天的理论和路线,最后由芒果打出了该跑法的完整路线(9月30日更新优化了路线,最后面的第二个墙角可以不用接触,从第一个墙角便可以直接飞到倒数第一个传送门前):
一.路线分析
新跑法全程不走传送门,为了减少速度损失在两个棱角尖处点地,跳过最后一个传送门后自然下落,待看到地面后执行飘浮操作
该路线最重要的就是最后一步操作,不能直冲冲的飞过去。错误示例如下
这场森林的结算时间是118.1,按照正常分数计算最后结果应该是2516-2517,但结果却是2510,差距不是一点半点。
森林的最终分数计算方法是分数+时间*10,既然时间没什么问题,那我们看一下结算分数

读秒表结束时显示的分数是1328。我又翻了一下其他2523的对局,发现他们的分数都是1336,这八分的差距从何而来?
新路线和老路线最后一段只有两个差距:高度(新路线高于老路线)和速度(新路线快于老路线)。为了明白是哪方面的问题,我做了两组实验:固定速度,控制高度,观察最后分数的差别
实验一:在坡顶开朱雀,结果:分数为1328
实验二:在坡底开朱雀,结果:分数为1336
那么结果就很明显了,影响分数的唯一变量就是角色的高度。在1920*1080的分辨率下,若角色和地面不在同一屏幕内,读秒表就会提前结束,分数减少8分,所以新路线选择了自由下落后进行飘浮,一方面,路线基本相同不会有速度损失,另一方面,高度适合不用担心分数损耗。
二.速度对比
路线问题解决了,下一步应该解决的便是速度问题。若是新跑法的最快速度小于常规跑法,那么上面的一切猜想和实验都不具有意义。
我用60帧的设备计算2524跑法最后一段的速度,从进入第二个传送门开始一直到最后结算,一共206帧,分数差值是94分,计算结果为2.191帧/分。若想超越2524,新跑法总体的速度平均值就必须比这个结果还要快
我们来测试一下切完流派后熊猫的速度(身位回退的路段已考虑,未进行计算)
选了两个视频进行对比
第一组:977分-1003分 分数差为26 所需帧数52帧 计算结果为2帧/分
第二组:970分-1002分 分数差为32 所需帧数64帧 计算结果为2帧/分
得到切流派后速度为2帧/分,明显要比最后一段走传送门的速度快。
我们换一种计算方式,若是全程不减速,保持2帧/分的速度一直跑到最后,所需的帧数是2*94=188帧,比常规跑法足足快了206-188=18帧,差不多0.3s的差距!
但这终究是最理想的状态。按照新路线的方法,角色需要点地八次,且最后的四个点跳都在上坡完成,任何一点失误都会造成速度的大量损失,这也让成功的难度直线上升。只有文字没有任何说服力,为了让大家更好的明了保速的难度,下面我辅以视频来计算肉眼难以判断的速度损失。
1.前两段点地:
分数段:1025-1085 ,分数差60,所需帧数120帧,计算结果:2帧/分
PS:插入一段科普,浮空板最后板边的判定空间比肉眼看到的更长,有时候感觉角色飞出去了,但是角色在判定空间内,仍然可以踩到板边,差不多这条红线范围内的空间都可以判定

回到正题,我们来看一下视频中两次点地的位置


可以发现角色点地特效的中心都在浮空板判定区间的最外端,属于比较完美的踩边,相当于接触地面的摩擦距离约等于0,速度几乎没有损失。
2.第三,四段点地:
分数段:1090-1157,分数差67 所需帧数138帧,计算结果为2.05帧/分,虽然减速了,但是损耗不大,无伤大雅。
PS:科普,当我们踩板边时,地面只会残留两个扇形的落地特效

当我们在平地点地时,还会多一个尖锥形的跳跃特效

跳跃特效 离 点地特效 的最右边界越近,则点地越趋近于完美。
这次点地后速度结果为2.05帧/分。
若是出现了失误,点地不是很完美,像下面这幅图,速度就变成了2.18帧/分

接下来的一次点地是踩板边,只要踩的完美,速度就不会有损耗(很显然这张图的踩边并不够好)
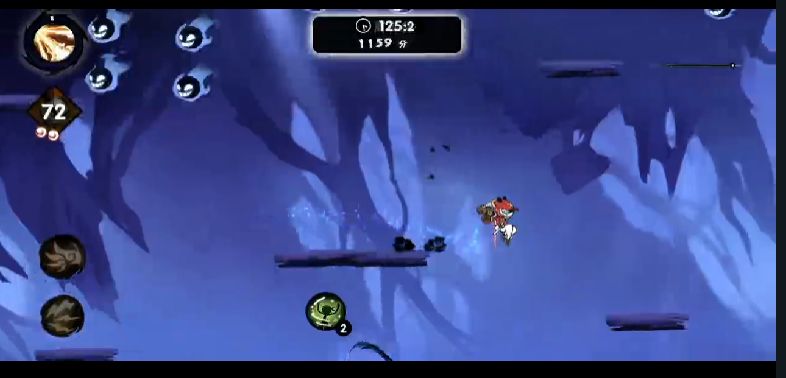
前四段点地总结:
共有三个板边一段平地,极限的板边点地速度几乎不变,完美的平地点地只有微乎其微的速度损失,也就是说四次点地只受到一次的影响,且影响效果不大
3.后四段上坡点地
前面的平地路段想要保持较小的速度损失还是比较容易的,但是后面的四段上坡让“保速”的难度直线上升。四个路段包括一个板边,一个墙角和两个纯上坡,且存在“只要与上坡有所接触就一定会减速”
PS:科普,浮空板下面是上坡的话,浮空板本身继承上坡的一切属性。
在平地上达到滑步最大速度后在上坡滑步会减速,当自身速度高于滑步最大速度而接触到上坡的话,减速效果成倍叠加:
①高速回归到滑步最大速度的减速
②上坡本体的减速
相关理论指路
忍三速度机制基础篇DLC-细碎知识点补充 - TapTap
https://www.taptap.cn/topic/21307616

至于上坡对速度的具体影响,视频如下:
第一段分数段:1160-1192 分数差32 帧数为68 计算结果为2.125帧/秒
第二段分数段(踩了上坡的浮空板后):
1195-1227 分数差32 帧数为76 计算结果为2.375
我们看一下踩板边的位置

可以看到这次踩边相对不错,但速度还是大幅减少,足以见得上坡减速的力度之大。
后面四段上坡点地如下图

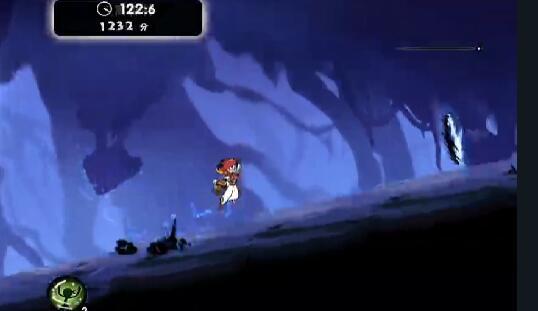

包括一个板边,一个墙角和两个纯上坡。按照保速理论,只要板边和墙角卡的极限,速度就不会有太大损失,但是两个纯上坡的减速却是致命的。由于我手里没有完美的后半段素材,所以无法计算每个上坡点地后的速度数据,但有一点肯定的是新跑法破纪录的难度已经达到了TAS(工具辅助竞速)级别。


