EH的数独杂谈#5 守护者(*)
2022/09/08741 浏览攻略
友情提示:
在阅读此篇章之前,笔者假定你已经了解了链的概念,以及上一篇提到的结论。
不过,这次要介绍的技巧并不是很常见。
--------
一、守护者的逻辑
二、死环
--------
这次要谈的是一个不算很常见的结构——守护者。
一、守护者的逻辑
如果你还记得上一篇介绍的连续环的性质,就会知道这样一条结论:由奇数个共轭对成环的结构是不存在的。这句话已经在无意间带出了守护者的核心逻辑。
直接上图,我们引用向神标准数独技巧教程的例题来具体说明一下:

如果两个橙色的4全都消失,会发生什么?r2c17,r4c7和r5c18的这五个候选数4,就会构成“奇数个共轭对成环”的情况(想想为什么会是这样?)。为了不让这种情况发生,橙色的4至少有一个为真。因此它们看到的位置的交集——r6c3,就不能为4。
我们可以看到,是这些橙色4的“守护”使得奇数个共轭对成环的情况不存在,这大概就是“守护者”技巧的名字由来吧。
二、死环
死环的逻辑和守护者无异。
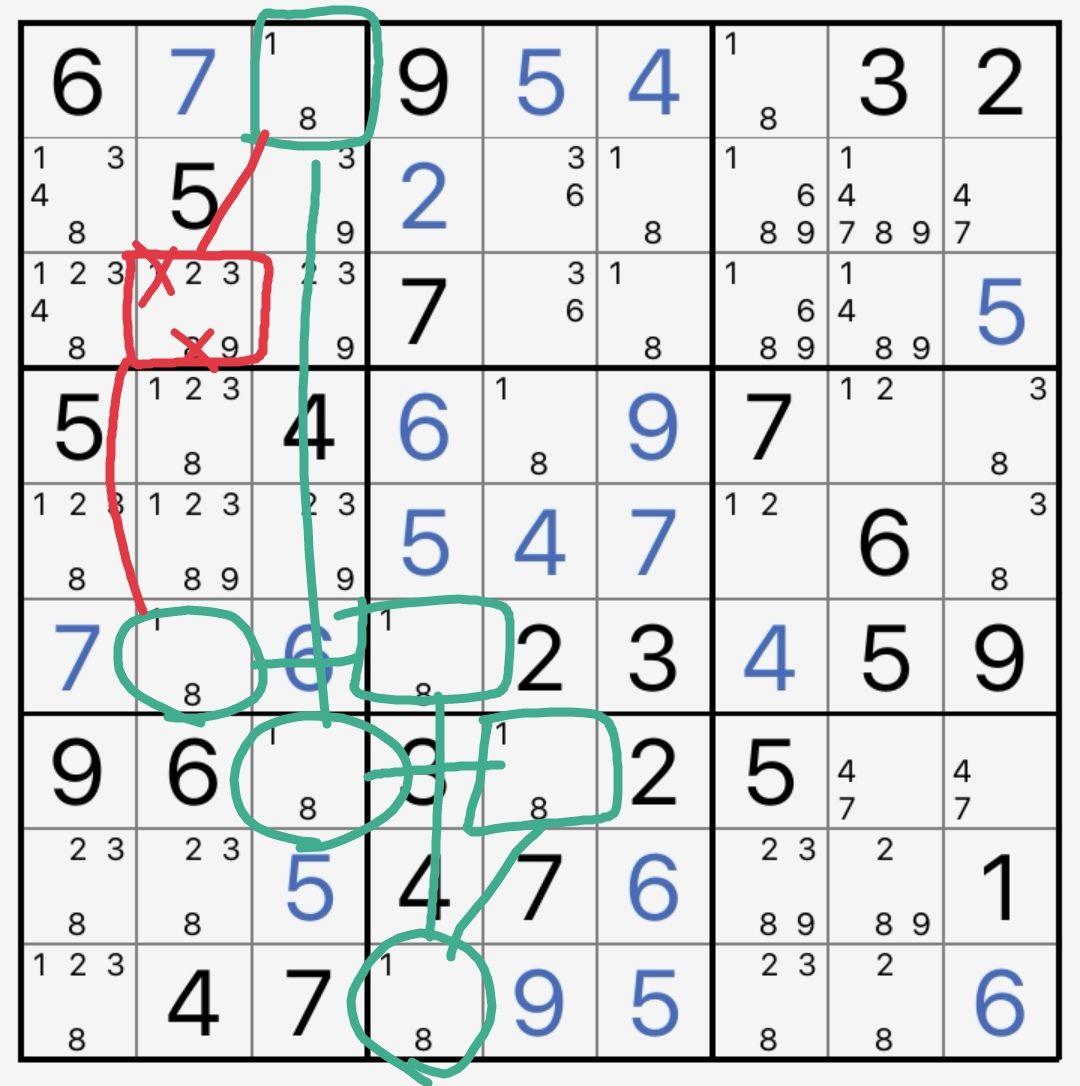
你已经在我之前的帖子里见过这个例子了。现在,我们从死环的角度分析一下。
我们注意到,有很多只包含候选数18的格子。如果红框内只有候选数18,那么无论对于数字1还是数字8,都会通过我图上画出的连接方式,构成“奇数个共轭对成环”的结构。这样,你在红框内无论填1还是8,最后都会产生矛盾。所以,r3c2自然就不能填18了。
或许你们注意到了,死环跟远程数对在形式上有些许类似,但其实逻辑是不同的。
--------
小结:
1. 由奇数个共轭对成环的结构是不存在的,这就是守护者的核心逻辑。
2. 死环是守护者的特例。



