下载手机 APP

EH的数独杂谈#2 标准链的反向延伸

2022/08/24577 浏览攻略

友情提示：

在继续阅读之前，请确保自己充分理解了上一节的内容，以及标准链（AIC）的基础知识。

--------

虽然标准链可以用来获取一些普适的结论，但在实际解题的过程中，找到一条能用的标准链并不总是很容易的事。

我们先来回顾一下标准链的使用方法吧。

一、标准链的基本使用方法

从上一节的探讨中我们了解到，形如A=B-C=D的交替推导链可以得到A与D至少一真的结果，也就是所有令A和D同假的事件都是不正确的。即使链再长，只要是强弱交替且以强链开始强链结束，则链头与链尾至少一真。现在对这句话做进一步分析：

（1）当链头和链尾是相同的候选数时，比如下面的例子：

TapTap

这条链写成文字是

r1c5(2=4)-r1c8(4)=r9c8(4)-r9c6(4=2)-r9c1(2)=r3c1(2)

（这里使用了简化的写法，也就是把一个双值格里的强链直接写在一个括号里）

可见r1c5(2)和r3c1(2)至少一真，也就是同时令这两个2为假的事件都是不成立的。什么事件满足这一性质呢？最容易想到的是两个紫色方框，如果这6格里有任何一格填2，那么r1c5和r3c1就都不是2了，不满足条件。因此这六格不能有任何候选数2，即r1c3≠2。

这里需要补充一个“看到”的概念。如下图所示，点选一个单元格（深蓝），那么与它在同一行，同一列或同一宫的20个格子都能被它“看到”。如果深蓝单元格填入一个数字，则被它“看到”的格子都不能填入这个数字；反之，如果这20格里存在某种数字，则深蓝单元格也不能是这个数字。实际上，我们在使用唯余时用到的也是这个思想。

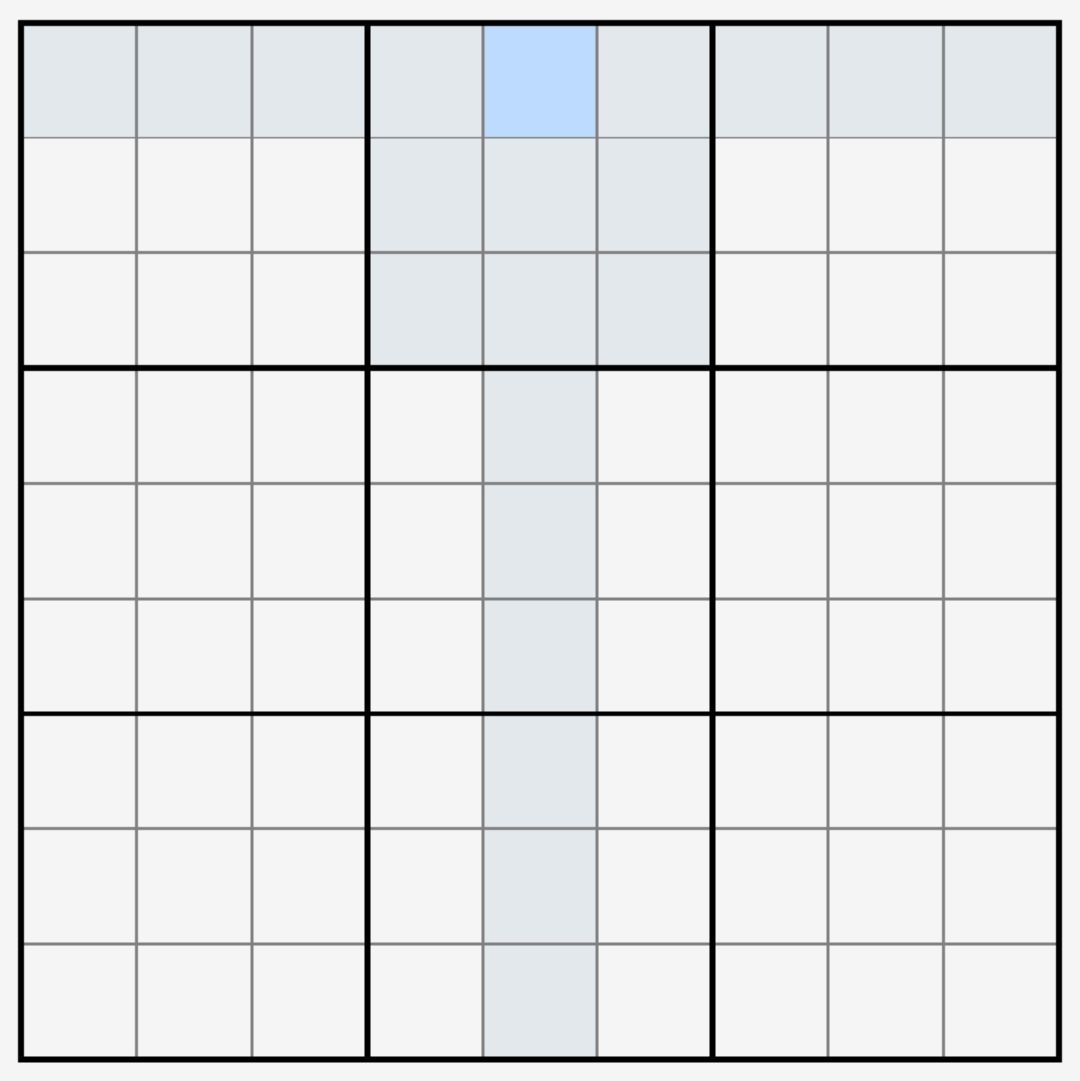
TapTap

回到刚才的例子，这样我们就会发现，只有紫色的6格是可以被r1c5(2)和r3c1(2)同时看到的。如果紫色格子出现了2，那么链头和链尾都不为真，这是不可以的。

所以标准链的使用方法之一是：如果标准链的两端是相同的候选数，那么其产生的删数是被这两端同时“看到”的单元格的该种候选数。

（2）当链头和链尾不是同一候选数，但是同区（希望你还记得“同区”的概念）时，如下图所示：

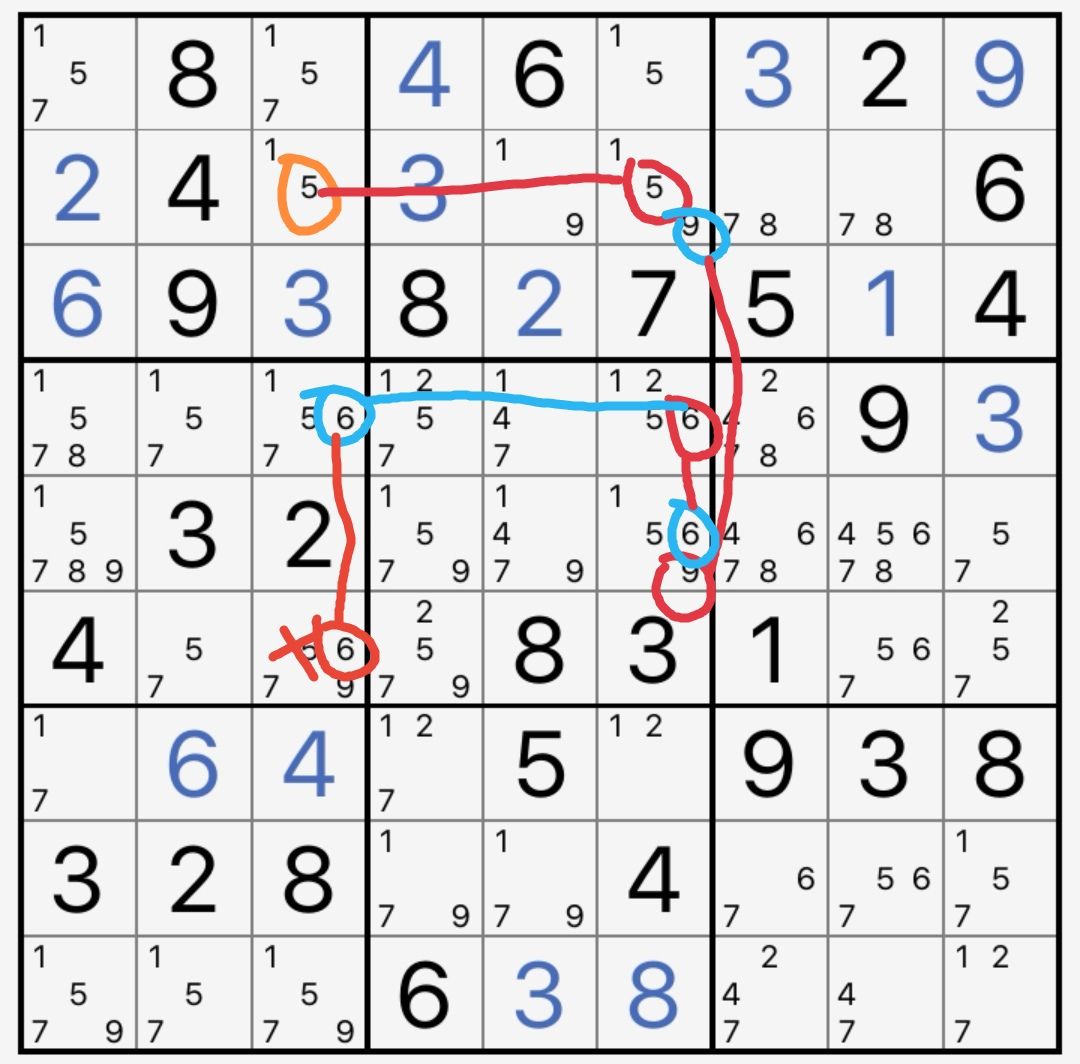
TapTap

这条链的文字表述是

r2c3(5)=r2c6(5-9)=r5c6(9-6)=r4c6(6)-r4c3(6)=r6c3(6)

注意到链头和链尾不是同一候选数，但位于同一列。什么条件可以让链头和链尾同时不成立呢？

如果在r6c3填入5，那么这一格（链尾）不能是6；由于链头也在这一列，所以链头不能是5，这样链头和链尾都不成立。这种情况不能发生，所以r6c3≠5。

从理论的角度上讲，由于链头A和链尾D同区，如果在A的所在格里填入D，则链头不是A且链尾不是D；如果在D的所在格内填入A，结论也是一样的。

因此得到标准链使用方法之二：如果标准链的两端是不同候选数但同区，则可以在“各自”的单元格里删除“对方”的候选数。

二、标准链的反向延伸

根据标准链的使用方法，要想用标准链来产生删数，要么保持两端同数，要么让两端同区，这是最有可能产生删数的策略。

尽管如此，有时候我们会发现自己选了个不太合适的链头，导致链在延伸的时候遇到尴尬的处境。比如，你从下面的题里找到了这样一条链：

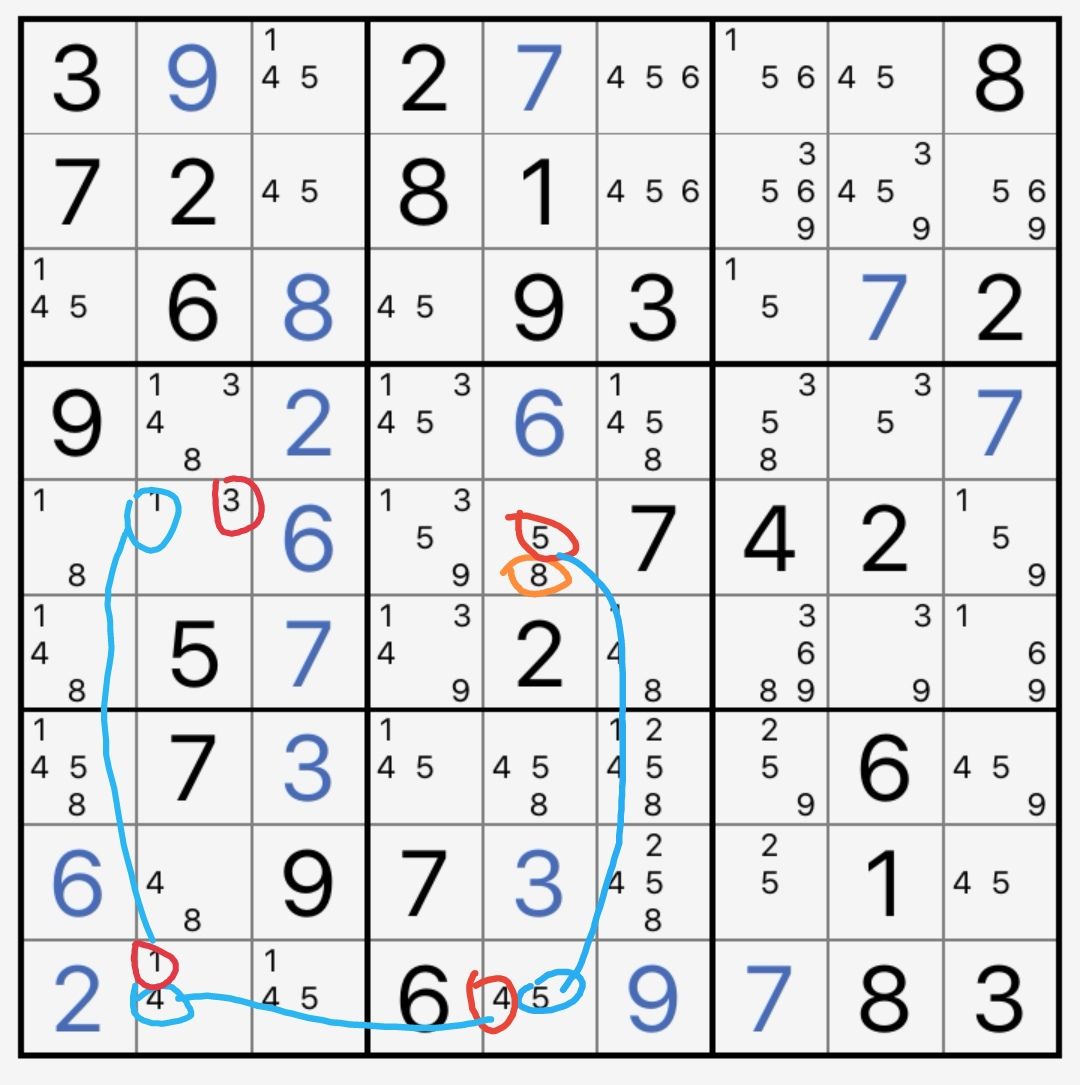
TapTap

r5c5(8=5)-r9c5(5=4)-r9c2(4=1)-r5c2(1=3)

现在已经是强弱交替的推导链了，但是没有什么结论，而且在r5c2(3)的这一端就很难继续推下去了。这时，我们可以考虑使用“反向延伸”的方法，也就是在r5c5(8)上做文章。

先从最简单的例子开始：一条链A=B-C=D，从D很难继续延伸。但如果我们设法从A端依次延伸出一条弱链和一条强链（也就是以A为真，推导结论）：

A-Z=Y

连接到原来的链上：

Y=Z-A=B-C=D

这样就变成了Y和D构成强链了。

我们现在对刚才例子里的r5c5(8)做类似的事情，不难找到

r5c5(8)-r5c1(8=1)

这样r5c1(1)就成了新的链头，将链变为

r5c1(1=8)-r5c5(8=5)-r9c5(5=4)-r9c2(4=1)-r5c2(1=3)

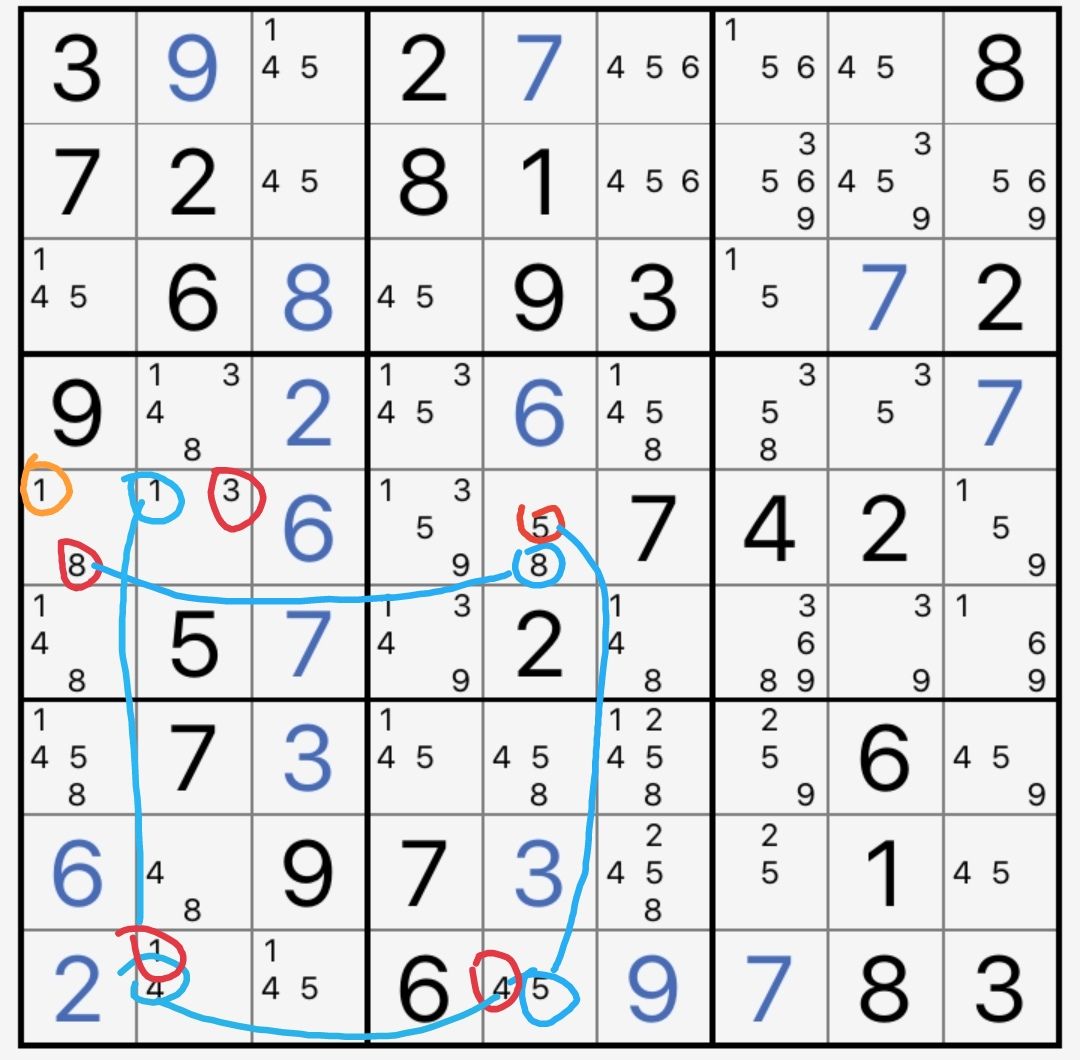
TapTap

于是r5c1(1)=r5c2(3)。根据标准链的用法之二，得到删数

r5c2≠1

实际上，考虑到交替推导链A=B-C=D本来就是很对称的，所以从A端延伸和从D端延伸没有什么本质区别。

--------

你可能会在其他教程里看到一些名词，比如XY-Chain（双值格链），自噬标准链等。它们是AIC的不同情况，基本逻辑是一样的。

数独清测试

9.2