EH的数独杂谈#1 再谈链的概念
2022/08/25671 浏览攻略
友情提醒:
笔者假设你已经仔细阅读过精华区“小灰的数独迷你课堂”系列,并且已经熟悉了数独的行,列,宫,单元格等概念以及链的基本概念。由于对这些概念的不熟悉导致的阅读困难,敬请出门左转。
--------
在最初了解到标准数独这一既简约又复杂的游戏时,你或许就已经听说过链的大名。链作为标准数独的一项重要技巧,可以用来解决相当一部分的难题,它的灵活性与强大的功能让无数数独玩家为之着迷。
但是,为什么数独技巧中要有链呢?
一、链的概念回顾
我们来回顾一下有关于“强链”和“弱链”的定义:
强链
第一定义:若根据候选数A(或B)为假可以推出候选数B(或A)为真,则A与B构成强链,记作A=B。
第二定义:若候选数A与B不能同时为假(至少一个为真),则A与B构成强链,记作A=B。
弱链
第一定义:若根据候选数A(或B)为真可以推出候选数B(或A)为假,则A与B构成弱链,记作A-B。
第二定义:若候选数A与B不能同时为真(至少一个为假),则A与B构成强链,记作A-B。
也就是说,这些定义都是用来描述两个候选数的逻辑关系。根据数独的基本规则,可以直接得到如下公理:
①同区(位于同一行,列或宫。这个概念很可能会在后续帖子里再次提及)的同种候选数两两构成弱链。特别地,如果这种候选数在这一区里只出现两次,则它们也同时构成强链。
②同一单元格的候选数两两构成弱链。特别地,如果这一单元格内只有两种候选数,则它们也同时构成强链。
③链没有方向性。
举一些具体的例子来说明一下吧,比如下面这个没有填完的盘面:
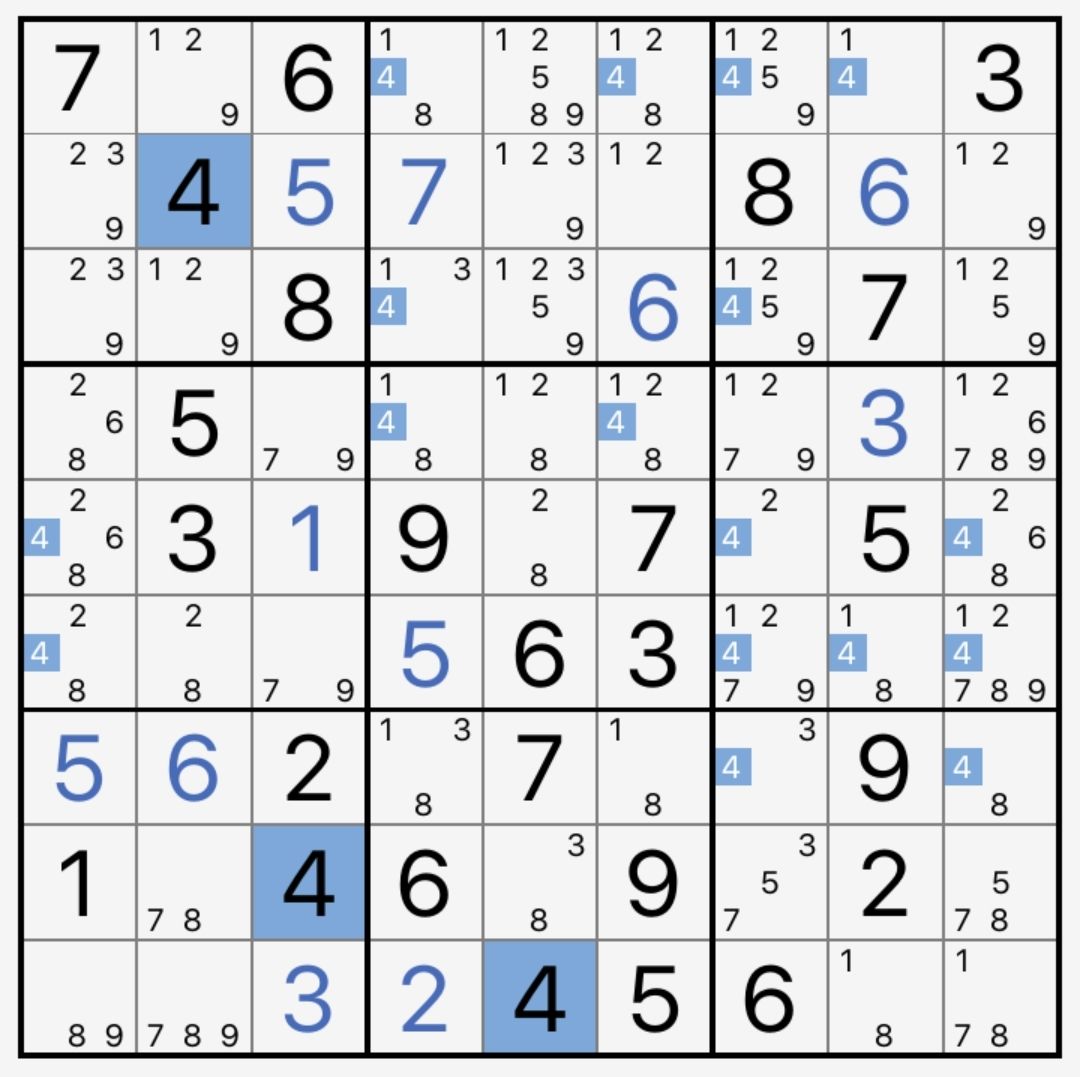
·对候选数4而言,注意到c4里有3格含候选数4,根据数独规则,这三个里只能有一个为真。所以从里面任意拿出两个,都最多只有一个为真。自然有
r1c4(4)-r3c4(4),r3c4(4)-r4c4(4),
r1c4(4)-r4c4(4)
·而在c6里只有2格含候选数4,那么它们有且只有一个为真,它同时满足强链和弱链的定义。自然有
r1c6(4)=r4c6(4),r1c6(4)-r4c6(4)
·如果聚焦于一个具体的单元格,比如r2c6,它只有1和2两个候选数,显然它不可能既是1又是2,即它们两个最多只有一个为真;同时它又必须是1或2中的一个,即它们两个至少有一个为真。因此它们既成强链又成弱链,即
r2c6(1)=r2c6(2),r2c6(1)-r2c6(2)
为了后续讨论的方便,我们顺便引入“双值格”和“共轭对”的定义:
双值格:如果一个单元格有且只有两个候选数,则这个单元格称为双值格。比如刚才的r2c6。
共轭对:如果两个候选数“有且仅有一个为真”(同时满足强链与弱链定义),则这两个候选数构成共轭对。比如r1c6(4)与r4c6(4),以及r2c6(1)与r2c6(2)。
此外,我们知道链是可以连接的。如果我们从r2c6的2开始,可以拉出一条这样的链:
r2c6(2)=r2c6(1)-r7c6(1)=r7c4(1)-r7c4(3)=r3c4(3)-r3c1(3)=r2c1(3)
在图上画出来大概是这样的。笔者通常采用手画,为了观察方便,用橙色圆圈表示链的开端,红线表示强链,蓝线表示弱链,叉号表示删数:
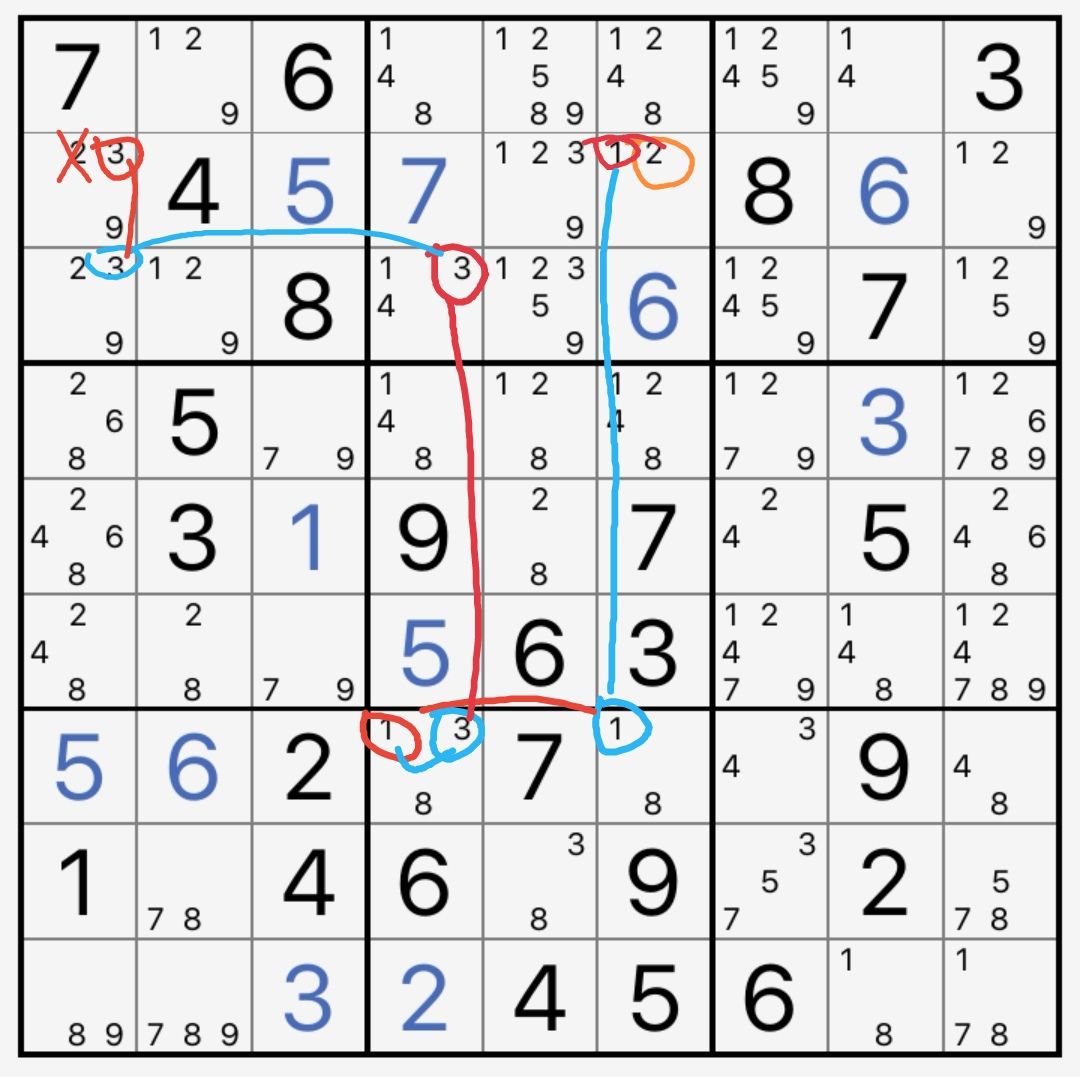
你会注意到,任意拿出一条短链都是正确的,而且整条链强弱交替,从强链开头,到强链结束。它的逻辑是,如果r2c6≠2,那么按照链的第一定义,可以一步一步推到r2c1=3,从而r2c1≠2;如果r2c6=2,那么还是有r2c1≠2。总之有删数r2c1≠2。
这种强弱交替的推导链简称AIC,它从链的基本概念中跳脱出来,变成了真的可以删数的实用技巧。
二、链与试数的关系
当然,你并不一定能一下子就想到用链来解题。在数独解到穷途末路的时候,你可能会采用“试数”的策略,即随手假设一个格子填某个数,一步一步推导下去,如果一不小心把这题解了,那为最好;如果发现矛盾,那就说明最初的假设是不对的。
还是拿刚才的例子,你假设r2c6是1,这样r7c6就不是1,那么r7只有一格r7c4能填1;从而r7c4不是3,c4里只有一格r3c4能填3...这个试数的过程是否可以用链来描述呢?
“假设r2c6是1,这样r7c6就不是1”——通过r2c6(1)为真推出r7c6(1)为假,根据链的第一定义,有
r2c6(1)-r7c6(1)
“...那么r7只有一格r7c4能填1”——通过r7c6(1)为假推出r7c4(1)为真,根据链的第一定义,有
r7c6(1)=r7c4(1)
连起来就变成了
r2c6(1)-r7c6(1)=r7c4(1)
从试数的过程看,我们从r2c6为1,推出了r7c4为1;从链的延伸看,从r2c6(1)依次经过一条弱链和一条强链连接到r7c4(1)。由此可见,试数中从一个数A为真推导到另一个数B为真的过程,就相当于从A依次经过一条弱链和一条强链连接到B。
按照这样的分析,你就可以从一个全新的角度去看我上面写的那条长链了,你试数的过程也终于可以用链的逻辑来完整地表述了。
不过,仅通过这点表述还并不足以让大家明白链和试数的区别。考察一个最基本的强弱强交替链
A=B-C=D
我们分情况来讨论一下:
①如果A为真,那么B可真可假,C可真可假,D可真可假。
②如果A为假,则B为真,进而“推出”D为真。
把这两个情况整合一下,就意味着A和D至少一者为真。
这个结论是不需要试数就可以知道的,完全正确的结论,因为在这一条链里就已经把A假和A真这两种情况都讨论一遍了。这意味着,如果数独盘面上存在一些事件让A和D都是假的,那这些事件是必然不成立的(无论A是真是假)。当然,你并不能仅从这一点就立刻知道A是真是假。
那试数呢?在试数的情况下,你更多地是在通过整个盘面的矛盾来反向检验最初假设的正确性。这意味着你必须先假定A是真或A是假。假设未必正确,那么得到的结论也就不都是正确的。
现在大家或许能够体会到了,链和试数虽有共性,但逻辑并不完全相同,使用方法和效果也并不相同。当然,这并不能说明试数在链面前一文不值,毕竟数独中仍然存在一些“不得不试”的灰色地带,仅仅用链来表述恐怕会太过麻烦了。
--------
希望上述内容能帮助大家更进一步地理解链的含义。如有错漏,请在下方评论区告诉我,你们的意见和建议是我进步的最大动力,谢谢大家!



