小灰的数独迷你课堂第十三讲——唯一性(Uniqueness)
修改于2021/05/082265 浏览攻略
前言:对于唯一矩形很多人都听过、用过。不过其实仔细讲起来,东西也不少。一些教程可能直接告诉你这个技巧,不过原理不怎么提,这一讲我试试看能不能讲一下。。。
首先唯一性的技巧基于标准数独只能有一个答案。(不过有部分观点认为数独可以有多解,所以唯一性的技巧在一些情况下无法使用)
唯一矩形:Unique Rectangle (UR)

看上面这个题目,剩下4个格子没有填,无论R2C1 = 6还是R2C1 = 8,这个数独都可以解决,符合数独的基本规则,同一行、列、宫都是 1-9 不重复。但这个数独有两个解了,他并不是一个合格的标准数独。
这个由两行两列构成的矩形我们可以直接叫UR,注意UR必须是在两宫内形成的。四个宫的情况并不成立。(很好理解吧。。。一个宫一个格的数难道不是确定的吗)
全双值坟墓:Binary Universal Grave (BUG)
BUG是UR的一种更加广泛的变形,所有候选数的格子都是双值,而且每个候选数在行、列、宫都只出现2次,这个数独要么有双解,要么没有解。
好了,上面说了这两种结构,但并没有任何的解题技巧,因为前面这两种结构都会导致双解,这并不是我们想要的,如果我们做的是标准数独(只有一个解),那么我们肯定不能让这样的结构出现,这样我们的解题方法就来了。
再次强调,下面的解法只能针对标准数独(只有一个解)
1. 全双值坟墓加1:BUG+1 - Binary Universal Grave + 1
什么是BUG + 1呢,BUG是指当你填完所有的候选数,已经无法再确定任何数字的时候,所有未填上数字的格子都是两个候选数,这样的结构是BUG(全双值坟墓),那当其中有一个格子是3个候选数,这样的结构是BUG+1。
BUG+1的解决方法很简单,我们需要避免这个数独成为BUG结构,所以应该把填上会出现 BUG结构的数字删除,简单理解就是那一个单元只出现两次的数字删除(或者说那个格子的数字就是那一个单元出现3次的数字)(你直接记成在行列宫出现最多的数字就好)
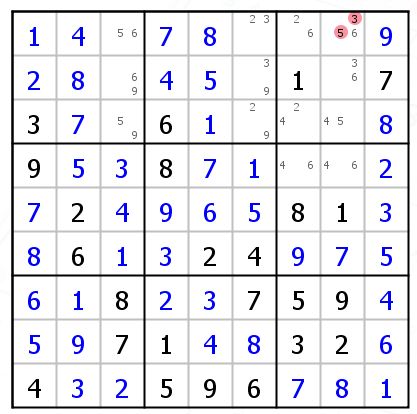
我们看这个例子。候选数只有一格是3个,再看看6在b3出现3次。直接填6.
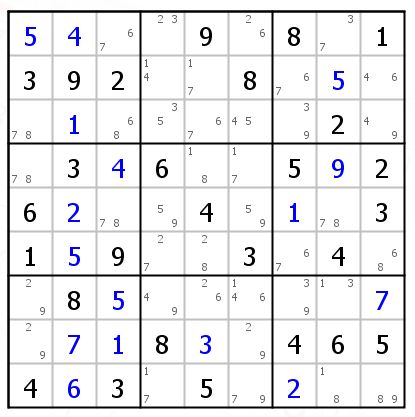
我需要说明一下,这个技巧很多人因为只是知道技巧,而不知道原理,所以会无脑用错。看这个例子,你可能会认为这是BUG+1,但是它不是!!!b8和c6里出现最多的候选数是9,而不是146中任何一个。说明的问题就是这个格中的候选数146并不会构成BUG。(形成BUG是因为9)
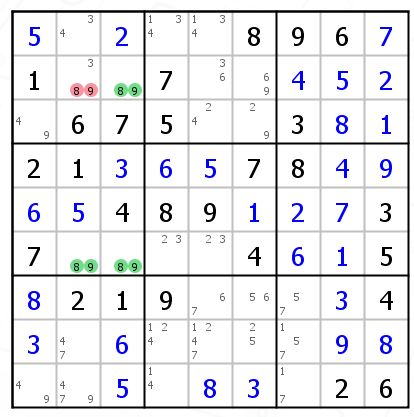
我们看个特殊的例子。(此例子出处为独·数之道论坛)这是一个BUG+2,R8C3和R2C8里面有两个3值,出现3次的数字都是4,我们要避免出现BUG,那么R8C3和R2C8的4至少要成立一个,用链来表示就是 R8C3{4}==R2C8{4},所以他们的交叉点可以删除。
2. 唯一矩形1型(Unique Rectangle Type 1)
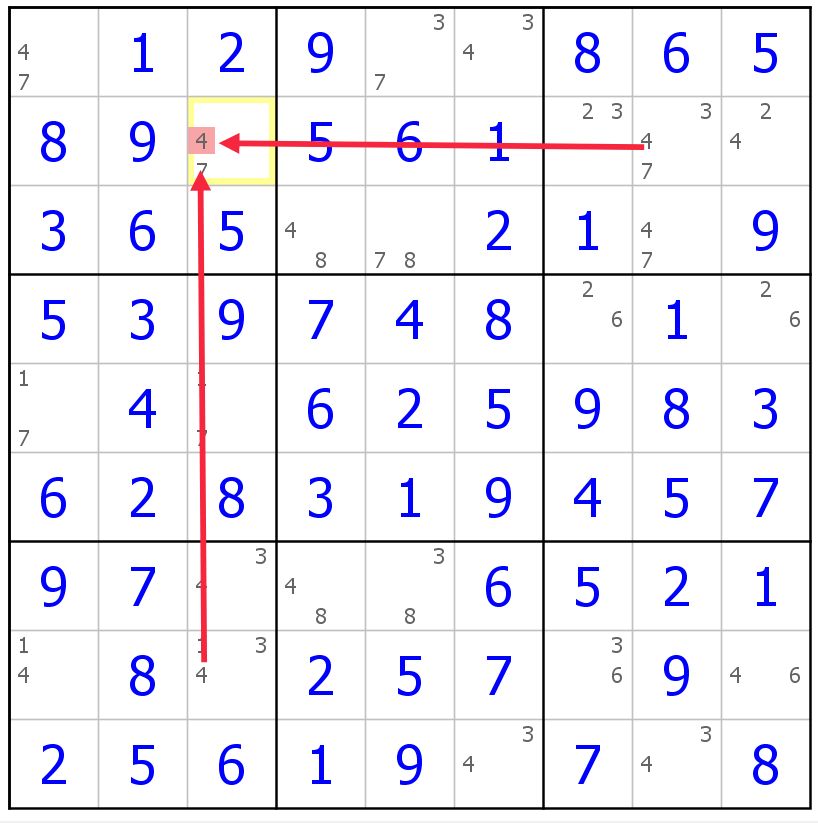
1型最基础。我们看如果r2c2≠3,那就是UR了。所以为了避免UR出现,就只能填3了。
1型就是这种4格就1格特殊,多出来其他的数,直接填多出来的数。
3. 唯一矩形2型(Unique Rectangle Type 2)
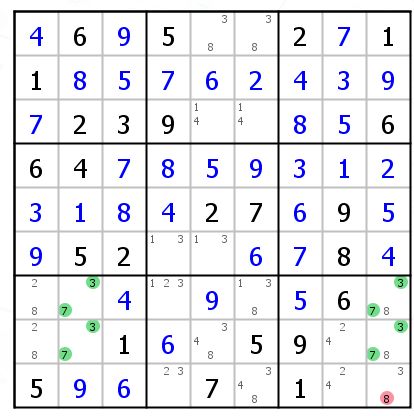
这个例子中,为了避免UR,c9r78必须有一个格填8,我们不知道哪个格填8,但是我们可以知道b9中其他格不能填8.(也可以排除c9其他格中候选数8,只是这个例子中没有b9以外的情况)
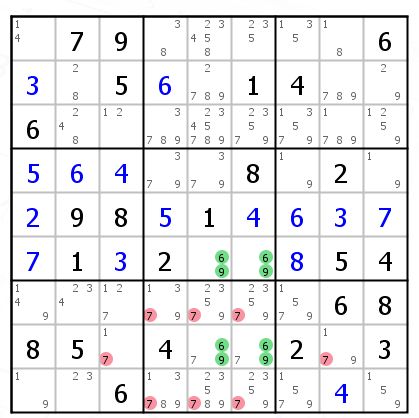
就比如这种情况,因为7必须在r8c56中,所以这两格共同作用的区域的候选数7都可以删掉。
2型就是4格中在一个宫的2格有相同其他候选数的情况,可以删掉其他格多出来的那个候选数。
4. 唯一矩形3型(Unique Rectangle Type 3)
UR 2型中,多出来的候选数是同一个数字,如果不同我们能做什么呢,看下面这个例子。
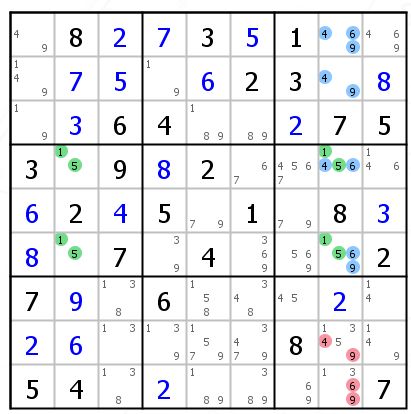
要避免出现15的UR,R4C8的46或R6C8的69必须成立一个,但这个看起来并没有什么用,结合R12C8这两个格,出现了一个469的数组,这几个数字在C8中必须出现在这几个格子,所以我们可以把C8中其他的469都删除。(其实就是把构成UR的15选择性无视,那么很明显构成了469显性数组,就可以继续了)
这种结构没法直接推出来数字和删除数字,但如果能在某行、列、宫找到和它对应的数对(数组),就可以删除那一行、列、宫的其他数字了。
3型就是4格中在一个宫的2格有不同其他候选数的情况,如果可以和其他格组成数组,就可以删数了。如果不构成数组是无法删数的。
5. 唯一矩形4型(Unique Rectangle Type 4)
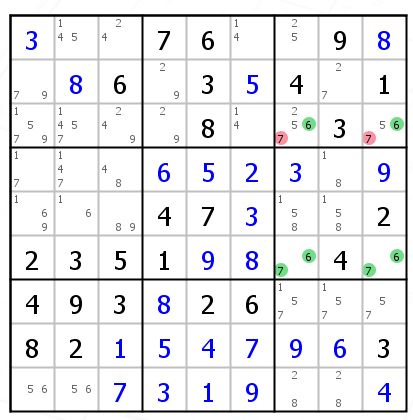
上图中我们要避免67的UR出现,那么R3C7的25或者R3C9的5要成立一个,R1C7 刚好是25跟他出现了数对,可以删掉R2C8的2,那么R2C8 = 7,两个红色的7可以删掉。我们再换个角度来看这两个7怎么删掉,如果R1C7不是25的话,观察R3,6只存在于这两个格子里面,所以这两个格子一定有一个6,另外要避免出现UR,这两个格子还需要有 25之间的一个数字,总共就两个格子,一个是6,一个是25中一个,7就没有地方放了,所以可以删掉这两个7。
4型就是4格中在一个宫的2格有不同其他候选数的情况,但是不像3型那样可以形成数组(不是对于这个例子,而是对于所有一般情况)我们可以考虑,既然多出来的候选数不知道怎么删,那我们就删构成UR的候选数(因为肯定有一个不成立)哪个数并不是这个构成UR的格独有的,就删哪个数。(上面例子6在b3就UR的两格有)
6. 唯一矩形5型(Unique Rectangle Type 5)
UR 2型中,多出来的相同候选数出现是在UR的同侧(同宫),如果出现在对侧(对角线)怎么办?
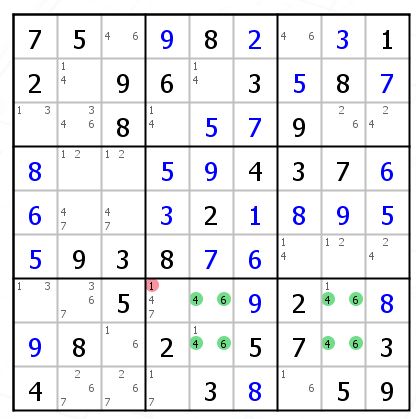
上图中,多出来的候选数1出现在对侧,这两个1一定有一个成立,这不就是一条强链么
R7C8{1}==R8C5{1},删除他们的共同作用格,上图中就是红色的1。
5型就是2型的变形,只是多出来的候选数出现在对角线上。原理类似,都是为了避免产生UR。
7. 唯一矩形6型(Unique Rectangle Type 6)
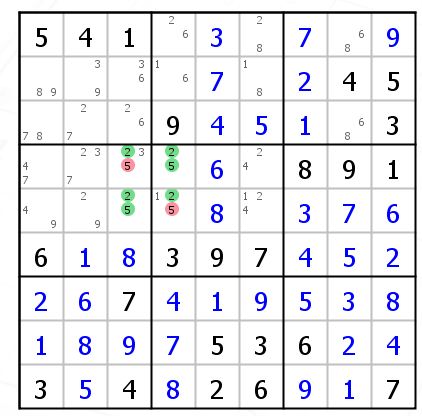
这个推断大家想想UR 4的方法,候选数5只存在于这4个格中。
要避免出现25的UR,那么这个矩形里面的13必须成立一个。对角线上的5是同真同假的关系,所以有13的格子就不能是5,如果是5的话,13就不能存在了。
6型就是4型的变形,只是多出来的候选数出现在对角线上。原理类似,都是为了避免产生UR。不过,4型删的是UR独有的,6型是非UR独有。原因很简单,4型是同宫,UR独有的只能出现在UR(因为该宫其他格填不了)而6型不是同宫,是对角线。UR独有的数在逻辑关系上是同真同假。(因为UR的其他两格填不了)所以只能删掉。(仔细想想)
8. 隐藏矩形(Hidden Rectangle)(又叫唯一矩形摒除)
在一个候选数是(AB) 的UR结构中,如果有2-3格有其他候选数,我们从没有额外候选的那一格开始,检查对角线上的格子数字A(B),如果那一格的行和列都不存在A(B),那么我们就可以删除数字B(A)。原理和UR 6差不多,我们看例子。
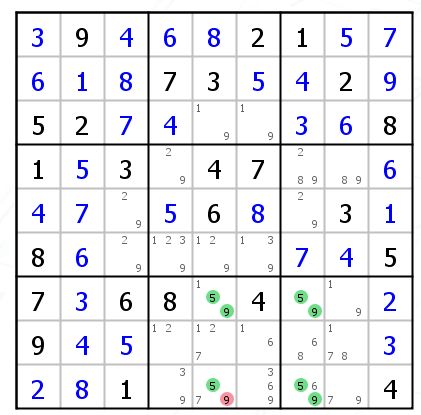
避免出现59的UR,176必须出现一个,R7C7的5和R9C5的5是同真同假的关系
假设 R9C5 = 5/7,那么 R9C5 肯定不是9
假设 R9C5 = 9,那么 R7C5=R9C7=5,R7C7是9,变成了一个UR。
所以 R9C5 的 9 可以删除。
再说一遍隐藏矩形就是从没有额外候选的那一格开始,检查对角线上的格子数字A(B),如果那一格的行和列都不存在A(B),那么我们就可以删除数字B(A)。
9. 可避免矩形(Avoidable Rectangle)
9.1可避免矩形1型(Avoidable Rectangle Type 1)
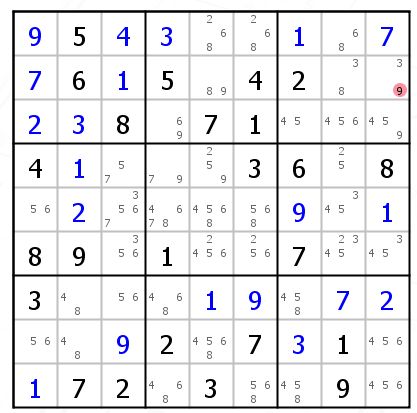
AR1类似于UR1,只是一个是填了数字一个没有填数字。R2C9如果填入9的话会发生什么,R1C1,R2C1,R1C9,R2C9出现了9,7,7,9 的一个UR,所以 R2C9 不能是9。
可能一开始不容易留意到。知道有这个技巧,或许会多注意一下。
9.2可避免矩形2型(Avoidable Rectangle Type 2)
AR1是一个候选数的情况,AR2是同侧单个候选数,类似UR 2。
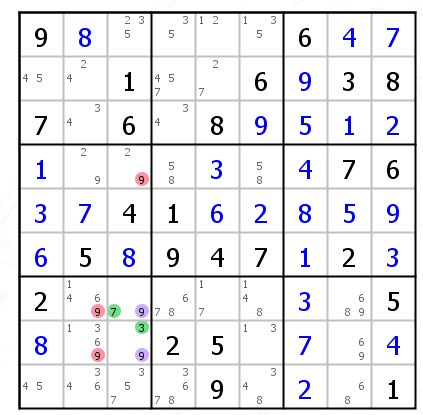
其实一样,紫色的两个9必须成立一个,不然就有37的UR了(r78c37)删除他们影响的 9。(类似9的区块)
对于可避免矩形,我需要强调一点。
数字必须是你填入的,不是数独题目已经给的数字,给的数字是不会动的,所以不是UR。
10. 残缺唯一矩形(Unique Rectangles with missing candidates)
(名字是我编的。。。不知道译名)
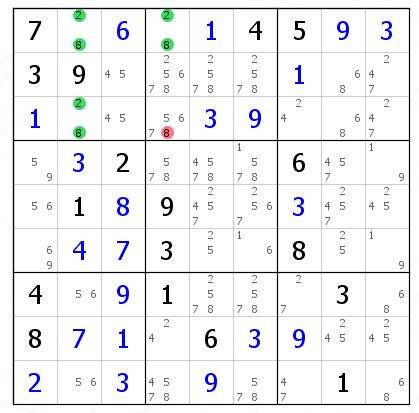
很好理解所以我不多说,没有译名或许是同一个原因。我们看到UR少了一点。。。r3c4没有候选数2.无所谓,没有候选数2是因为之前我们的操作删掉了,而不是这个格因为现在行列宫有2而不能填。我想你已经猜到我要干什么了。那我就填一个候选数2呗,这就完美了。此时就是UR1型。(1型是删掉UR的两个候选数,如果是3个候选数就直接填不是UR的那个,如果有3个以上候选数那就保留呗)
其他类型同理。我是不会再举十个例子的。
习题1:
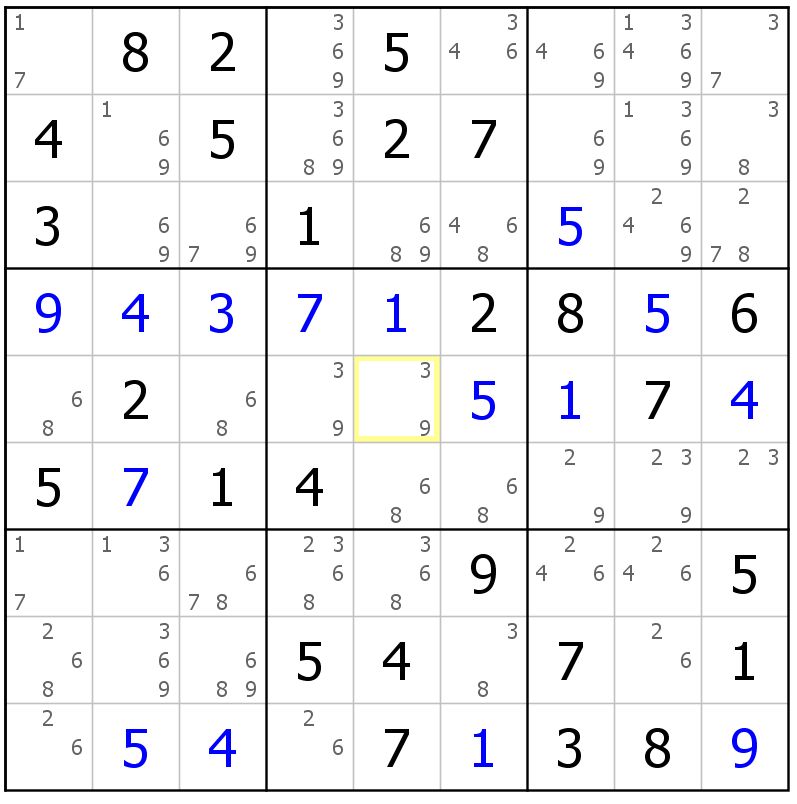
用本讲技巧进行删数(69)
习题2:
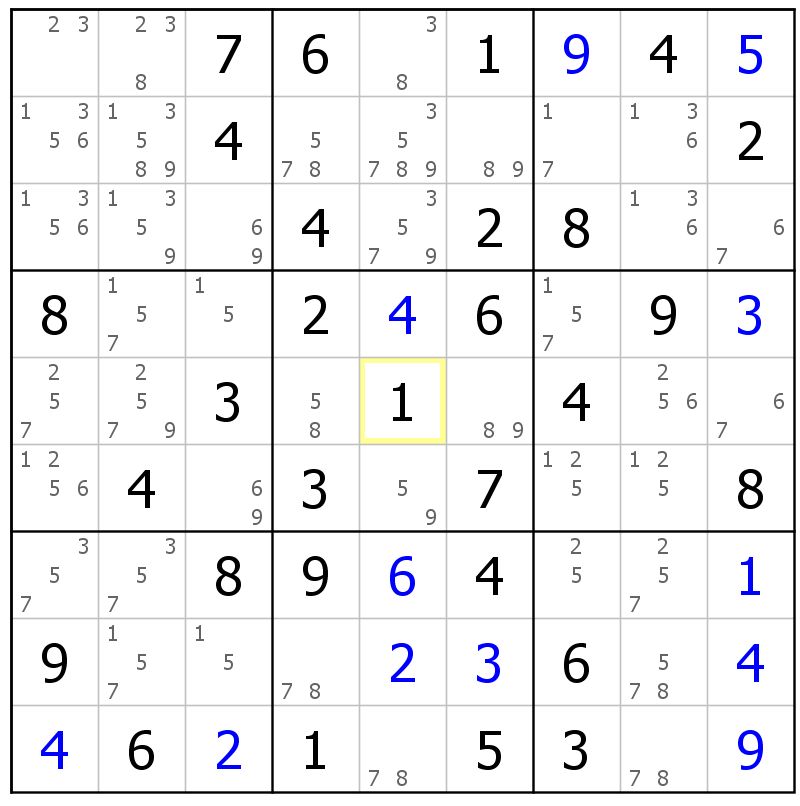
同上(15)
总结一下,就是避免UR的出现。要么删除构成UR的候选数,要么删除构成UR格的非候选数共同作用的区域。
注意:
1.此方法只适用于标准数独。(解唯一)
2.UR的构成是在两行两列两宫,而不是四宫。
3.如果不确定是否可行,就不要轻易删。
4.使用BUG+1时注意,并非所有情况可用,该数必须满足所在行列宫出现最多。
答案见回复,附上总集篇链接。


