复制闪电和扭曲时空的收益计算
修改于04/05860 浏览综合
前置概念:
物种等级:
等级 名称
22 母体
21 清理者
20 毁灭者
19 机甲兽
18 生化兽
17 霸王龙
16 始暴龙
15 甲龙
14 巨鳄
13 大鲵
12 大白鲨
11 盾皮鱼
10 文昌鱼
9 珊瑚虫
8 草履虫
7 孢子
6 古菌
5 蓝藻
4 支原体
3 DNA
2 原子
1 原子核
主物种:在合成过程中,消耗雷电的速度大于雷电生产速度的等级最高的物种。
次物种:比主物种等级高1级的物种。
例如:在不断合成珊瑚虫的过程中可以耗尽雷电,并且不断合成文昌鱼的过程中雷电有剩余,那么就说珊瑚虫是主物种。文昌鱼是次物种。
另外称次物种是主物种的父物种,主物种是次物种的子物种
在游戏的绝大部分进程中,当一个物种刚刚成为主物种,使用复制闪电收益更高。到达某个阶段后,将所有主物种转化合成次物种,使用扭曲时空的收益更高。本文目标是根据当前游戏主次物种的数量以及生产等级复制等级等多个参数,比较复制闪电和扭曲时空的收益,对游戏策略进行优化。
1.
收益公式的推导
推导过程以主物种是珊瑚虫为例,其他阶段只需要带入相应等级的物种的数据即可。
雷电产速e
智慧产速w
科学加成s(科学加成51%则s=0.51)
珊瑚虫等级u
珊瑚虫数量m
珊瑚虫复制等级p
文昌鱼等级v
文昌鱼数量n
文昌鱼复制等级q
文昌鱼生产等级t
复制闪电的收益
复制闪电直接的收益为奖励的闪电,需要把这些闪电转化成珊瑚虫的数量。按理说这个阶段文昌鱼种群数量不成规模,但是在不清楚游戏规则的情况下,是有可能在这个时期消耗资源去提升文昌鱼的种群规模的,加上推导过程需要的变量本来就会涉及到文昌鱼的数据,额外计算文昌鱼生产珊瑚虫并不会增加程序的复杂度,索性一并将其算进去了。此外,这个时候盾皮鱼以及比盾皮鱼等级更高的物种可能解锁也可能没有解锁,就算已经解锁,它们的种群规模数量级比文昌鱼更加低,要计算这部分收益的话需要的变量要还要增加额外物种数据,会增加推导过程和程序编写的复杂度,但对结果的影响微乎其微,所以不计算盾皮鱼及比盾皮鱼等级更高的物种带来的收益。
首先是一次性奖励雷电生产速度10万倍数量的雷电,考虑科学加成,这部分雷电的数量表示为:
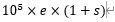
使用这部分雷电来合成珊瑚虫,默认情况1雷电合成1珊瑚虫,珊瑚虫复制等级每提升1级,雷电合成珊瑚虫的数量x2,所以这些雷电合成珊瑚虫的数量为:

生产12000智慧需要的时间表示为12000/w,文昌鱼生产珊瑚虫的基础速度是10/s,这个数等于文昌鱼的等级v,文昌鱼的生产等级每提升1级,生产速度x2,所以文昌鱼生产珊瑚虫的速度可以表示为:
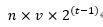
文昌鱼在这个时间内生产的珊瑚虫数量可以表示为:
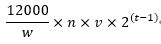
因为扭曲时空的收益使用文昌鱼的数量增加量比较方便计算,为了和扭曲时空的收益做比较,模拟计算这两部份的珊瑚虫可以转化成多少文昌鱼,默认情况下合成1文昌鱼需要消耗1e10的珊瑚虫,指数10等于文昌鱼的等级v,文昌鱼的复制等级每提升1级,同等数量的珊瑚虫合成的文昌鱼数量x2,所以两部分珊瑚虫转化成文昌鱼的数量可以表示为:
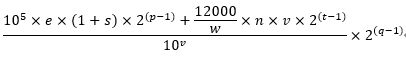
扭曲时空的收益
扭曲时空每次消耗500智慧,为了和复制闪电收益做比较,需要进行扭曲时空24次,不可以简单的通过将将扭曲时空1次的收益乘以24得到,因为每次扭曲时空后,将扭曲时空这个过程生产的雷电全部用来合成珊瑚虫,加上文昌鱼在这个过程中生产的珊瑚虫全部合成了文昌鱼,下一次扭曲时空的时候,文昌鱼的生产效率有所提高,每次扭曲时空的收益都会比上一次扭曲时空的收益更高。
这个过程就像在银行存钱计算利息的单利模式和复利(利滚利)模式。银行年利率1%,存100块钱,单利模式就是按年利率1%存够24年,取出来的时候本息一共124元。复利模式就是先存一年,取出第一年的本息101元,再存入银行,第二年取出本息102.1元,再存入银行…这样到第24年取出来的时候,本息一共就是126.97元,虽然从结果上看一共差了不到3元钱,那是因为这里基数小,从相差的比例来看,复利模式的利息比单利模式的利息高了12.375%,在基数足够大的情况下,这个差距是不可忽略的。
扭曲时空一次奖励的时间15分钟等于900s,在科学加成下等于900*(1+s),生产500智慧需要时间500/w,所以一次扭曲时空等效的流逝时间可以表示为:

推导的时候先假定文昌鱼的初始数量是已经将所有珊瑚虫转化成文昌鱼之后的数量。这一步骤可以在计算程序中进行预处理。
先计算在一个扭曲周期时间内文昌鱼生产的珊瑚虫数量.将这部分珊瑚虫又全部合成文昌鱼,合成得到的文昌鱼的数量为可以表示为:
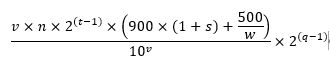
另一方面这个时间周期内雷电系统生产的雷电数量:
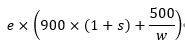
这部分雷电用来合成珊瑚虫得到珊瑚虫的数量:
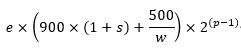
将这部分珊瑚虫用来合成文昌鱼得到文昌鱼的数量为:

这样一个扭曲周期内的文昌鱼增量可以表示为:
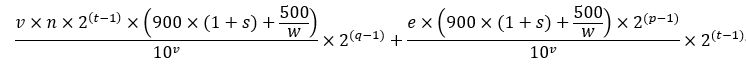
简化后等价于:

进行下一次扭曲操作的时候,除了文昌鱼的初始数量不一样之外,其他条件完全一致。所以24次扭曲时空文昌鱼总数量的增加可以表示成:

ni表示第i次扭曲时空操作时,文昌鱼种群的初始数量。
公式虽然看起来复杂,但只需要推导一遍,在计算机的帮助下,这种复杂程度的计算只需要一次简单的鼠标点击就可以得出结果。用js写一段程序来分别计算复制闪电的收益和扭曲时空的收益,并用html写一个简单的可视化界面:
这是计算收益的两个方法的核心代码:
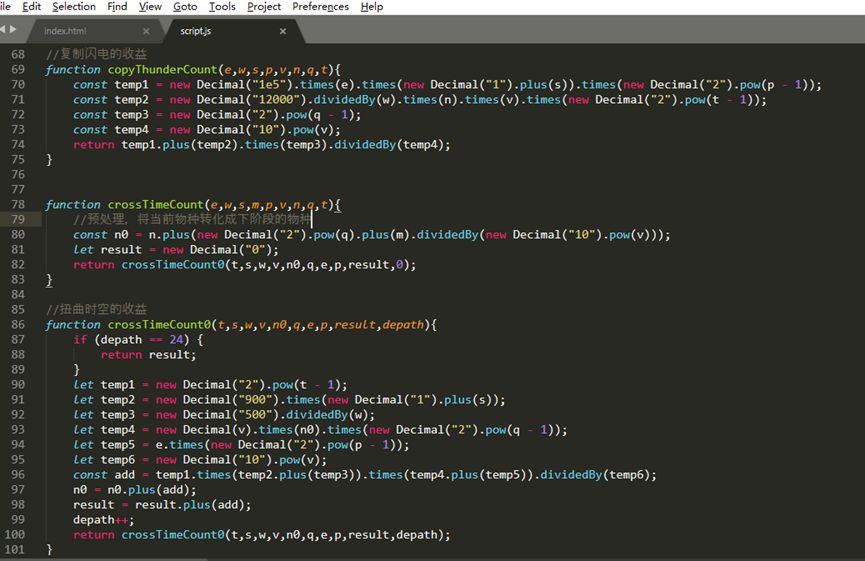
将当前游戏进度中的实际数据填到对应的输入框中,点击计算即可分别得出复制闪电和扭曲时空的具体收益,从而选择对应的策略。

补充说明:在实测过程中发现一个问题,前面推导的扭曲时空收益,需要在智慧刚满500就进行扭曲操作,但实际情况这个收益很难达到,因为很难做到时时监控着智慧看着它刚满500就进行操作并持续24次,前面的推导过程得出的结果是扭曲时空的理论收益上限。
举个例子,当智慧已经累计到12000的时候,已经够扭曲24次了,但是由于没有及时进行操作,假设生产500智慧需要的时间是T,在连续扭曲24次的过程中,和理论推导的过程相比,除了第一次扭曲收益相同以外,第二次扭曲就没有享受到第一次扭曲结束后到第二次扭曲之中间生产500智慧需要的挂机时间T的加成,第三次就没有享受到第一次到第三次中间生产1000智慧需要的挂机时间2倍T的加成,以此类推…为了让这个工具的计算结果更加具有参考性,现在对计算工具功能进行补充,不仅计算出扭曲时空的理论收益上限,还将模拟真实情况中智慧累计超过500时候操作的收益:
每存500智慧扭曲操作:500档(收益上限)
累积1000智慧扭曲操作:1000档
累积2000智慧扭曲操作:2000档
累积3000智慧扭曲操作:3000档
累积4000智慧扭曲操作:4000档
累积6000智慧扭曲操作:6000档
累积12000智慧扭曲操作:12000档(收益下限)
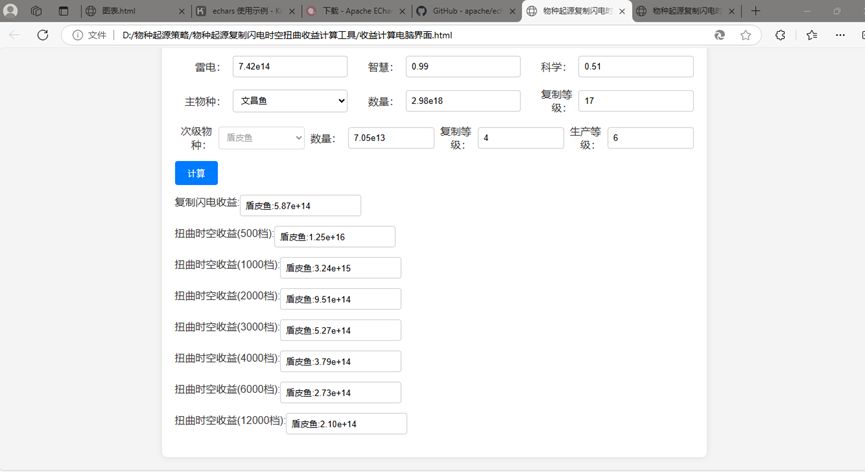
以这张图为例,我是根据我当前的游戏进度的数据进行输入计算,这个时候我已经存了12000智慧,虽然我现在时空扭曲理论收益上限是1.25e+16,但是这个收益需要从当前时间开始,每次刚攒500智慧就进行扭曲操作,并持续24次才能达到。如果这12000智慧直接用来扭曲的话收益将缩水到2.10e+14,还不足复制闪电收益的一半。所以我这个时候的最优策略是直接将12000智慧拿来复制闪电,先将闪电全部转化成文昌鱼,再合成为盾皮鱼,接下来再等待生产500智慧一次一次的进行扭曲操作。
补充:在将公式编写成计算程序过程中因为优先级的的关系导致程序计算结果错误,现已修正,并打印一些中间结果辅助分析。同样以上图中的状态为例,修正后的程序计算结果:




