从概率分析许负强度

修改于2025/03/211019 浏览综合

关于许负的讨论，几乎都指向了超模，我也是这个观点。但我依旧认为，从概率角度分析许负的强度，有助于在泡沫破灭后依旧保持理性的认知。

从家仆阵的角度来看，如果允许携带同类型的多个名臣，那么阵容搭配的可能性将会指数型上升。许负就是这样的一个发动机，相较于春秋战国演义而言，甚至允许同类型名臣的家仆同时上场。这无疑为阵容配队开拓了空间。

但是许负是从你所拥有的所有名臣中随机抽出五位，而无悔至今已有203位名臣了。刨除许负本身不可被发现，将彩蛋角色“王上”计入的话，假设一位玩家拥有无悔迄今以来的所有名臣，且各名臣被抽到的概率相等，且利用相面技巧使每次相面必定成功，则我们可以进行以下计算。接下来的推论都基于本段的这几个假设。

推论一：许负难以定向抓人

让我们建立许负抓人的数学模型。我们可以运用排列数来计算许负抓人的概率。经过计算，这一概率为2.5%，sl次数的数学期望为39.6次。具体计算过程将会在下文给出。显然，这并不是我们想看到的结果。

推论二：扩大名臣选择可以有效降低sl次数

如果我们不苛求某一名臣，而是将名臣的选择范围延伸至较强的一系列名臣中（假设有m个），这样，我们可以计算出许负相面中的名臣中有这m个指定名臣中至少一个的概率为：

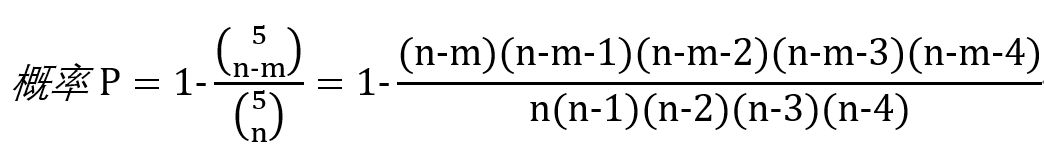
sl次数的数学期望为：

其中，n等于许负相面池中角色个数。下文n默认取203。推论一是该公式中m=1时的特例。

计算可得：m=5时，P=0.118，E=7.45次；m=10时，P=0.225，E=3.44次；m=15时，P=0.32，E=2.11次。

由此可知，扩大名臣选择池可以显著降低sl次数，从而显著提高游戏体验。

推论三：先带许负相面，最后带名臣进场

假设在军事位上存在A、B两位名臣，其配合存在强度。若我们在携带许负的同时携带A或B进场，则计入m中的只有未被选中的那个。但是，若我们先携带许负而不携带A、B中的任何一位，则A、B同时会被计入m中，从而在不影响配队思路的情况下提高了m，从而提高选中概率。

总结

通过简单的概率计算，我们轻而易举地开发并证明了许负的更优玩法。希望这些推论对你的游戏过程有所帮助~

猜你想搜

无悔华夏许负强度分析

7.3