无悔战斗系统的数学模型
修改于昨天 16:58124 浏览综合
从简单的军规、战力,到通过战斗能力判别胜负,再到攻击、防御、回复等属性的大量出现,本文旨在提出一个较为通用的无悔战斗系统数学模型,将无悔中常见的各类属性归纳于统一的数学模型中,通过数学推导与实战经验,将对胜负的判别从定性推进到定量,也即计算出各类属性等同于多少的战力加成、战斗过程中存在多少战损,从而为名臣排行、剧本运营和战斗策略提供理论依据。
本文的模型构建得到了群大锤,时不时遇上镰刀(雨神二群群友)的大力支持。笔者与其在这一周相对独立地分别推导出了大部分结论,相互印证了该模型的正确性。其也摸索出了物资车所给钱粮的计算公式,这个公式可能未来也会通过这样的帖子,在摸索完一整个体系后系统性地发布。
本文的模型也引用了沉默的告白所给出的格挡衰减公式与防御减免公式。
本文的数学模型推导上有部分步骤涉及高等数学内容,考虑到大多数人没有必要知道推导过程,我会直接放公式和对应的推论,而推导过程放在文后,以供质疑与参考。
本文的数学模型尚有不足之处,欢迎评论区的各位进行补充说明。
无悔战斗系统的数学模型
无悔战斗系统的数学模型的核心是一个概念:战斗力值。其定义为:

其中,公式中所涉及的“单体”概念由来如下:无悔战斗中最小的战斗单元是兵团里的小人,这个小人就被称作一个单体。在出征时,每个兵团都会依据其兵种类型和分到的军规而分为若干个单体,单体再根据军队战斗力和其分到的军规决定其攻击力、防御等。单体的攻击力等属性一经分配,便不会由于其本身血量的下降而下降。由此,我们给出下列定义式:

关于单体个数,有以下表格以供参考,空格处数据可自行根据比例关系推算:

也可推导出一个定律:战斗力值差值定律,即战斗过程中双方战斗力值的差值不变。例如:我方战斗力值为M,敌方战斗力值为N,则M-N=P,P为战斗结束后我方留存的战斗力值。由于P的计算公式中大概率只有一个变量“军规”,因此,我们可以粗略计算出一场战斗后胜者留存多少军规。
一些有趣的推论
推论一:攻击、攻速百分比加成折算战力公式:
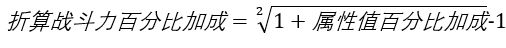
属性值包含:攻击、攻速等,仅可在单一变量时使用
例如:我方军团+100%攻击后,折算的战斗力百分比加成为(1+100%)^0.5-1=41.42%;
推论二:战损的计算
设虎队战斗力为250,军规为50000;鹊队战斗力为200,军规为25000。双方皆为车兵,均只有一队兵团,在浅水进行肉搏,双方不使用任何卡牌,不考虑士气因素带来的军团行为,问虎队战损多少?
解:题设条件符合使用简略公式的条件,即战斗力值=0.5*战斗能力^2*兵种生命成长*兵种攻击成长*单体攻速*攻击系数/(1-免伤系数)。设虎队战斗力值为M,鹊队战斗力值为N,显然:虎队获胜,故P为虎队剩余战斗力值。
双方同除无关系数后得到:(250*50000)^2-(200*25000)^2=(250x)^2,x为虎队剩余兵甲数。
解得x=45825,战损为8%;实机多次测试,结果在13%附近上下浮动,基本符合理论运算结果。
推论三:叠战斗力军规阵容死路一条
自家仆被大量开发以来,大量的低战损乃至无战损阵容出炉,这些阵容不在本数学模型的讨论范围之内。但我们可以证明:这些阵容较传统叠数值阵容有显著优势。
陈庆之是这些低战损阵容的影响者之一。一般认为,如果一个阵容能够长期维持5%以内的战损,那么使用陈庆之便具有较高的收益。让我们来计算一下如果一个纯数值阵容想要符合陈庆之条件,需要叠到多高的数值。
不妨假定我方战斗力为p、敌方为q;我方军规为a、敌方为b,其余属性符合简略公式要求。那么,根据战斗力值差值定律,(ap)^2-(bq)^2≥(a*0.95p)^2,解得ap≥3.2bq,即我方战斗能力应至少是敌方的3.2倍,才能在单次战斗中将战损降低至5%及以内。且随着累战,军规也会衰减地越来越快。
让我们考虑挑战模式内常见的开局情况:敌方ai战力为300,我方基础战斗力为200,双方军规相等。若想将战损降低至5%,则我方战力需叠至3.2*300=960点,需要额外获取760点战力,至少需要7个祖冲之。随着ai战力的爆发式增长,这个数字还会不可控制地膨胀。然而,这对于大多数家仆阵容来说,是较为简单的战斗情况(逆战100,50%)。因此,我们应当自然而然地意识到:纯数值名臣的强度与家仆、机制名臣已经存在一条不可逾越的鸿沟了。因此,我们不必带着对旧有观念的固执,应当让纯战力军规名臣下放。
推论四:高贵的连锁
上文提及,单体的输出不因其血量降低而降低。因此,在面对短时间大量伤害时,若伤害不致死,则将伤害均摊至每个小人身上时可以有效避免军团总体输出因此降低。例如:枪兵的枪阵、骑兵的冲锋都是通过短时间的大量伤害快速击杀一部分敌方军团的单体,从而打出先发优势。而若军团连锁,则可以减少单体数量的损失,同时为回复争取时间和空间。
理论推导
兰彻斯特方程
兰彻斯特方程是描述交战过程中双方兵力变化关系的微分方程组。在无悔中,绝大部分战斗情况符合兰彻斯特平方律。其理论推导涉及常微分方程的计算,具体过程可自行搜索,我这边打公式太累了![[表情_微笑]](https://img.tapimg.com/market/images/0f170d4b1ecf80c267e5a44b5992a199.png)
![[表情_微笑]](https://img.tapimg.com/market/images/0f170d4b1ecf80c267e5a44b5992a199.png)
战斗力值概念与离散化
详见《游戏设计战斗过程的基本数值知识与理论》(网易公司 宋悦)
战斗能力概念
详见《【无悔华夏】战斗力、军队规模、兵种等级与战斗能力》(itsafool)(其实就是我本人)
护甲的计算
由于无悔的小兵的输出不因其血量下降而下降,我们可以认为:护甲就是假血。因此,护甲值可以直接相加于单体生命之上。
回复的计算
如何刻画回复是一个较为困难的问题,因为其不仅发生在接敌时,也发生在脱战时,而这与战场上的双方兵种、双方士气、士气打击、移速等息息相关。笔者能力尚不足以将其纳入模型考虑范围之内。因此,我们只计算接敌时的回复功效。这代表这通过该模型计算出的回复功效为其下限,而其上限的相当大一部分取决于操作者的操作能力与地图地形等等。若接敌时敌方不卡在回复cd间集火我方某一单体并致其死亡,我们可以认为其相当于在计算完攻击力后又减去了一部分。由于攻击力最少为1且为了维持战斗力值差值定律的有效性,该模型对于回复的计算需要满足以下条件:敌方回复值≤(战斗力*军规系数*兵种攻击成长-敌方防御)*攻击系数*(1-敌方免伤系数)-1;回复值≤(敌方战斗力*敌方军规系数*敌方兵种攻击成长-防御)*敌方攻击系数*(1-免伤系数)-1。此后的计算无太大意义,可谓是“垃圾时间”,对于大多数阵容来说也已近乎于战斗的结束,故剩余时间的回复量忽略不计。
免伤系数的测算
详见《无悔华夏格挡衰减公式,充分了解自己的免伤数值》(-沉默的告白-)



