下载手机 APP

EH的数独杂谈#15-2 五星题002

修改于2024/12/07527 浏览攻略

返回传送门：

#15 五星题全解析

题目信息：

【SE评级】8.3

【HoDoKu评分】3504

第2题的初盘如图15-2.0.1所示。经四大基本技巧整理，得到如图15-2.0.2的盘面。

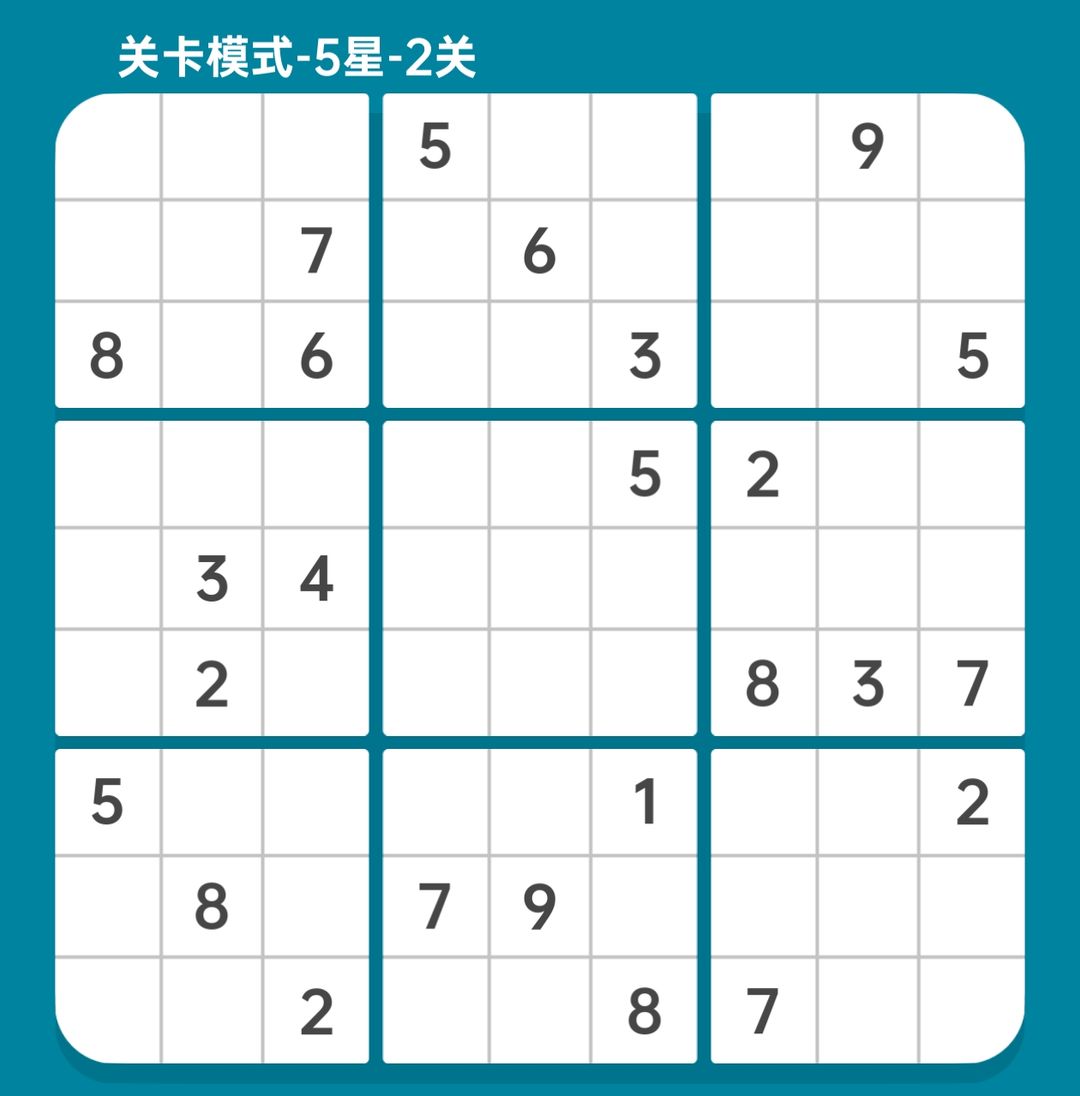
TapTap

图15-2.0.1 初盘

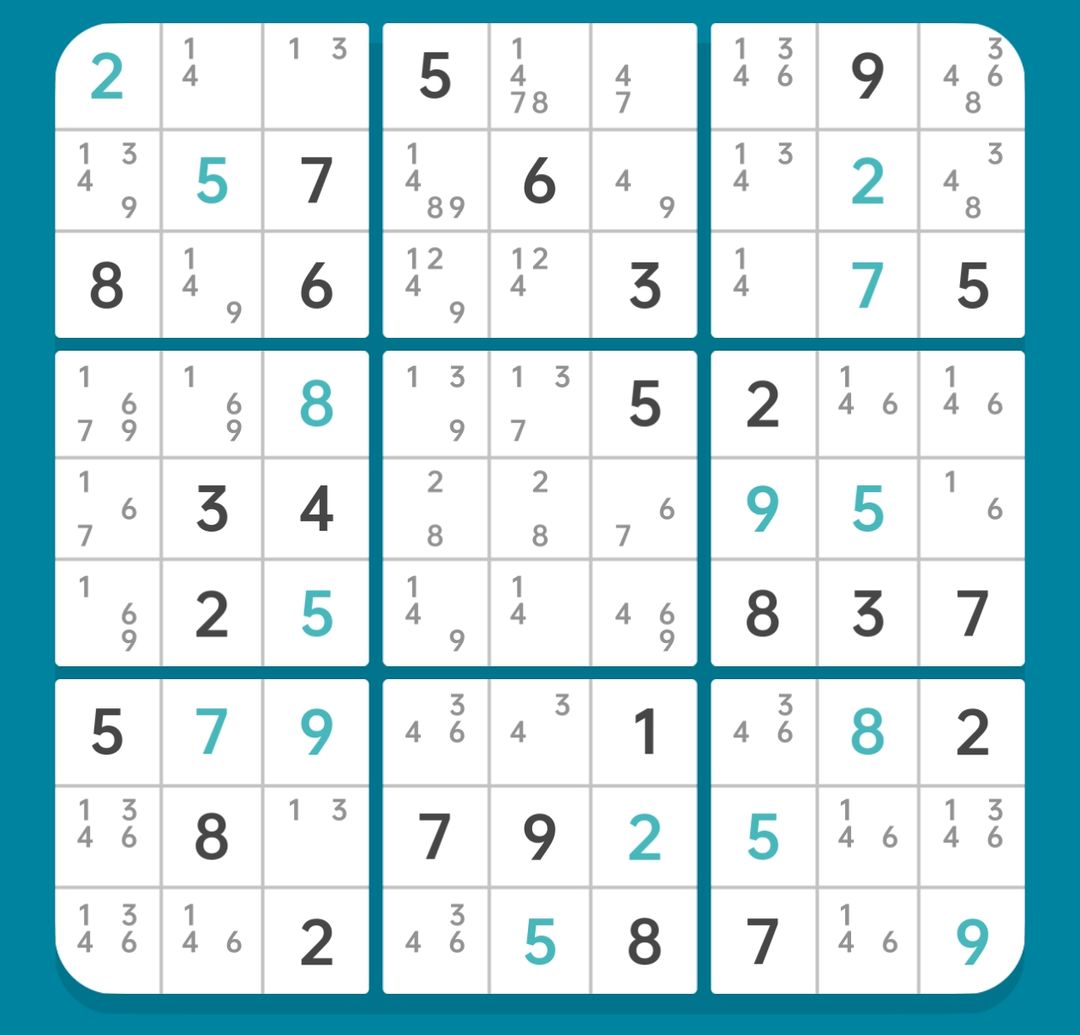
TapTap

图15-2.0.2 初步整理后的盘面

Step 1 鳍三链列

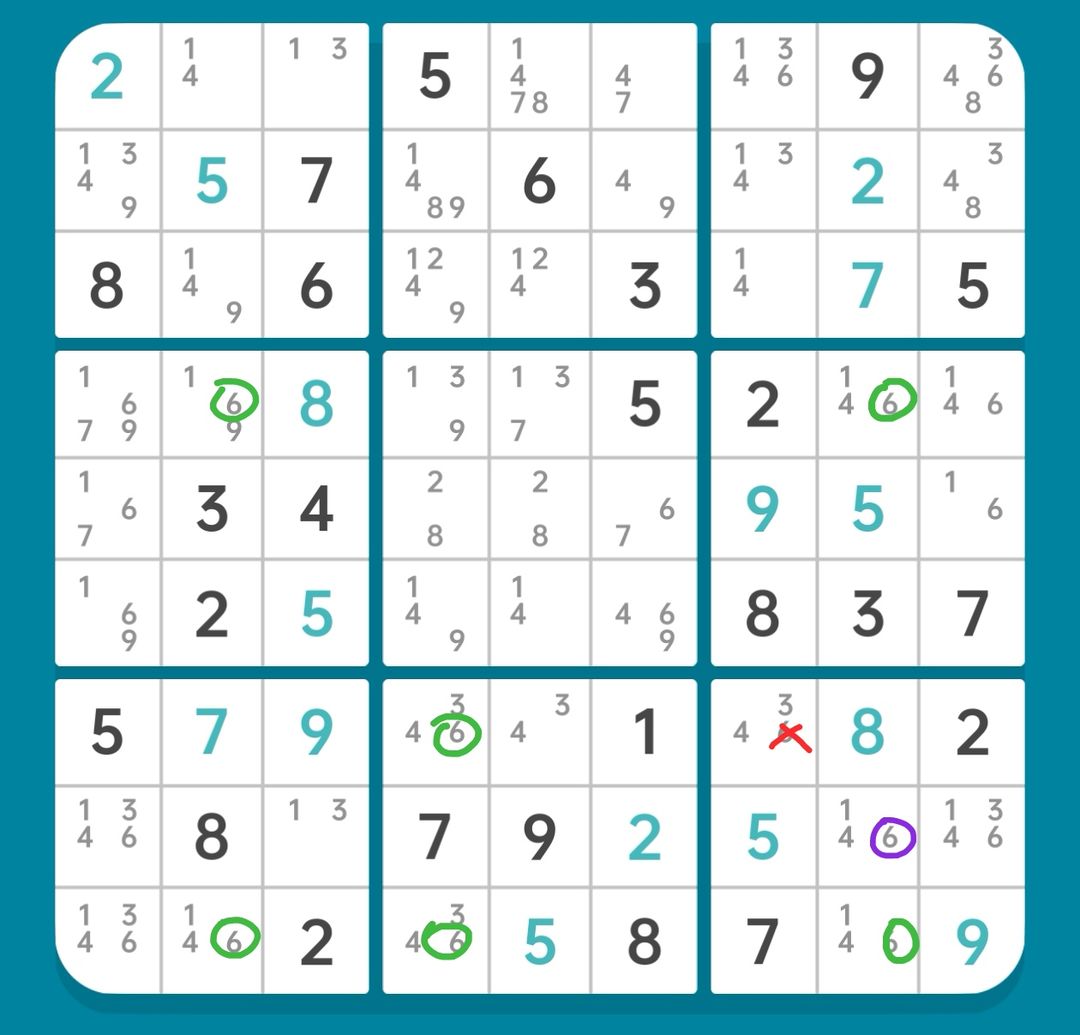
TapTap

图15-2.1.1 鳍三链列

如图15-2.1.1，我们分析c248三列的6，可以找到以r8c8(6)为鳍的鳍三链列。

【删数】r7c7(6)

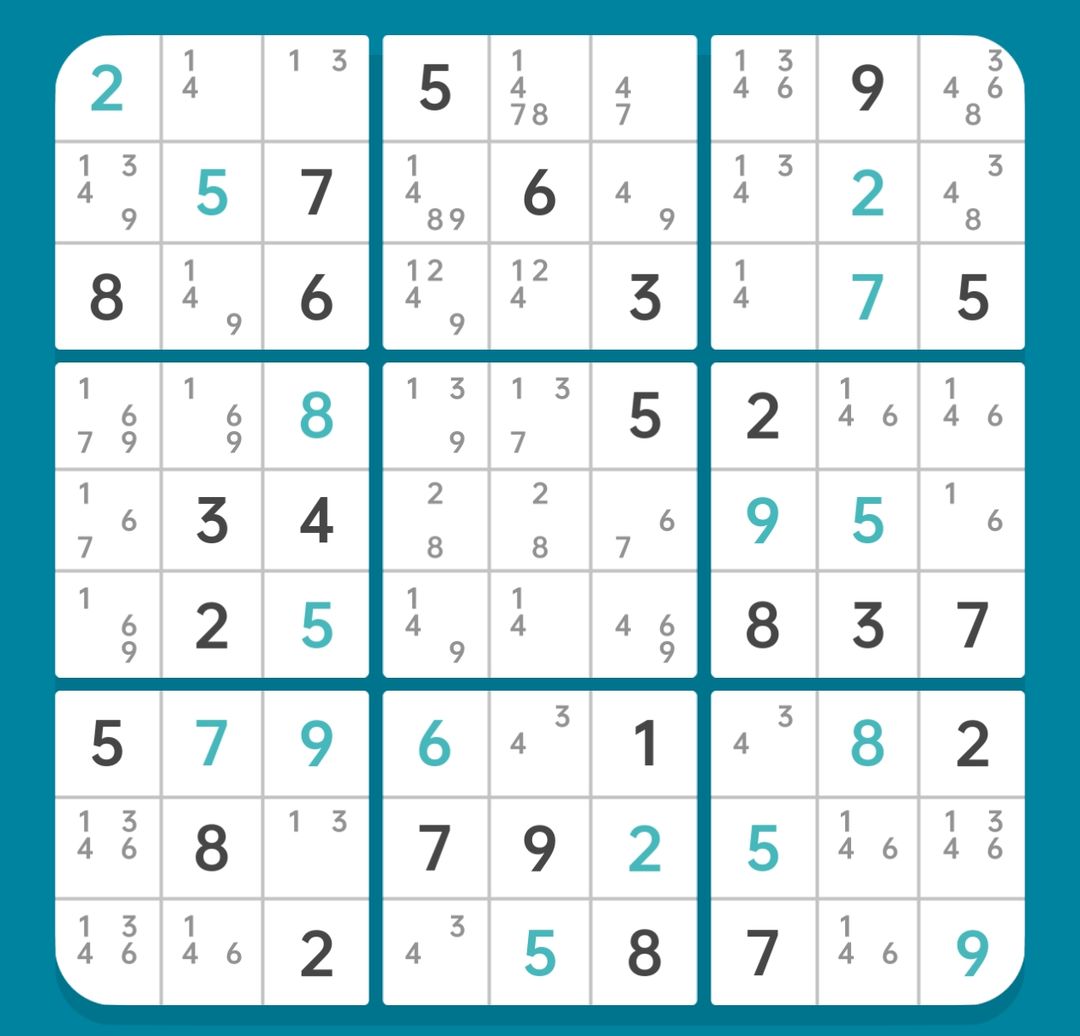
TapTap

图15-2.1.2

Step 2 AIC

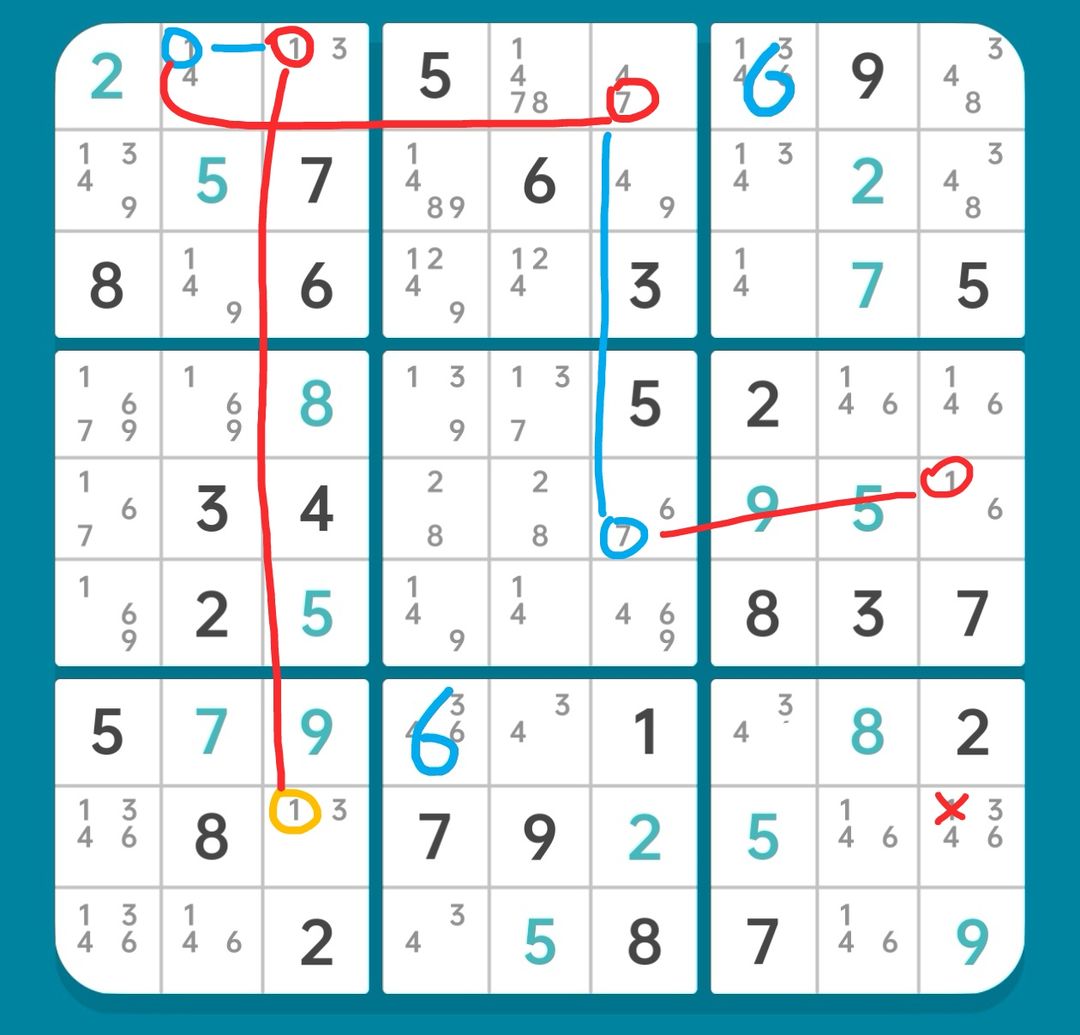
TapTap

图15-2.2.1 AIC

如图15-2.2.1，找到如下链：

r8c3(1)=r1c3(1)-r1c2(1)=r1c6(7)-r5c6(7)=r5c9(1)

【删数】r8c9(1)

TapTap

图15-2.2.2

Step 3 刺连续环

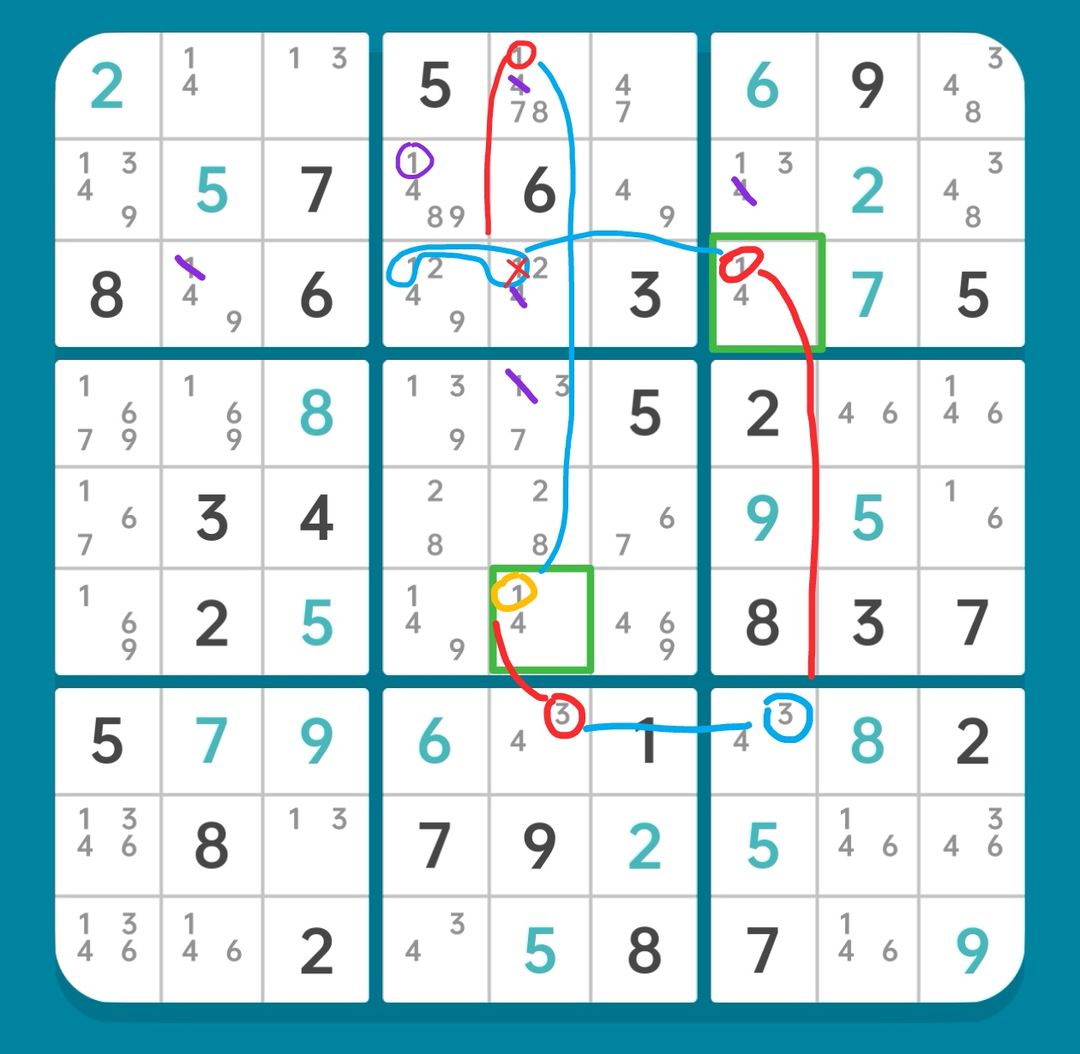
TapTap

图15-2.3.1 刺连续环

这是本题的一个主要难点。首先我们根据两个绿框以及7行的4强链，发现W-Wing的存在，从而有强关系

r6c5(1)=r3c7(1)

进一步地，如果r2c4(1)不存在，则这两个1也同时构成弱关系。于是我们有了一个以r2c4(1)为毛刺的连续环：

r6c5(1)=r7c5(3)-r7c7(3)=r3c7(1)-r3c45(1)=r1c5(1)-r6c5(1)

有如下预备删数：

r13c5(4)，r2c7(4)，r3c2(1)，r4c5(1)

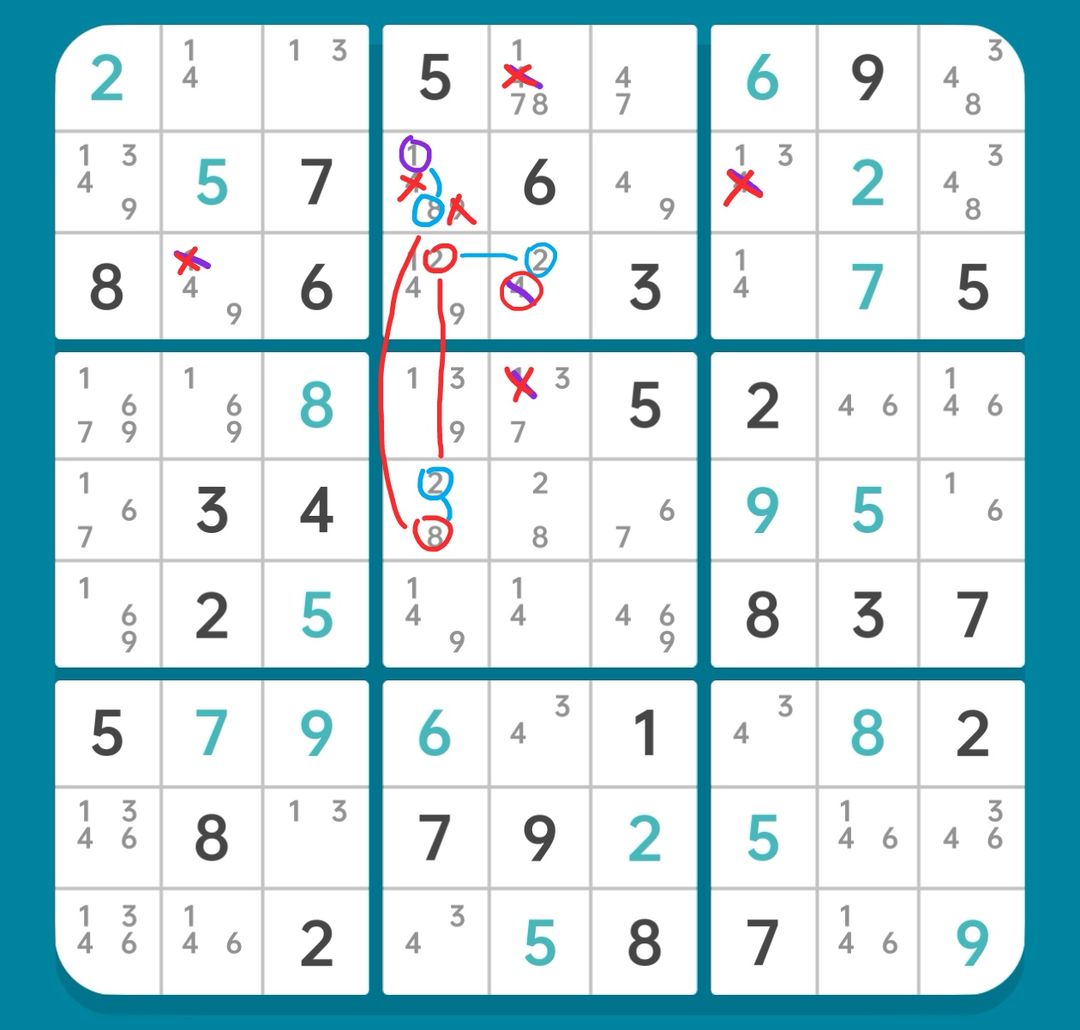
TapTap

图15-2.3.2 刺真返回预备删数

接下来看看刺为真时发生什么。如图15-2.3.2，由r2c4(1)真，可以引出强制链

r2c4(1-8)=r5c4(8-2)=r3c4(2)-r3c5(2=4)

也就是通过r2c4(1)真，我们推出了预备删数r3c5(4)真。根据刺连续环的性质，原环及刺的推理路径上，除了r3c5(4)以外的非同源预备删数均可删除（秩理论的内容，如果不理解也可以一路推到底）。

【删数】

r1c5(4)，r2c7(4)，r3c2(1)，r4c5(1)；

r2c4(49)

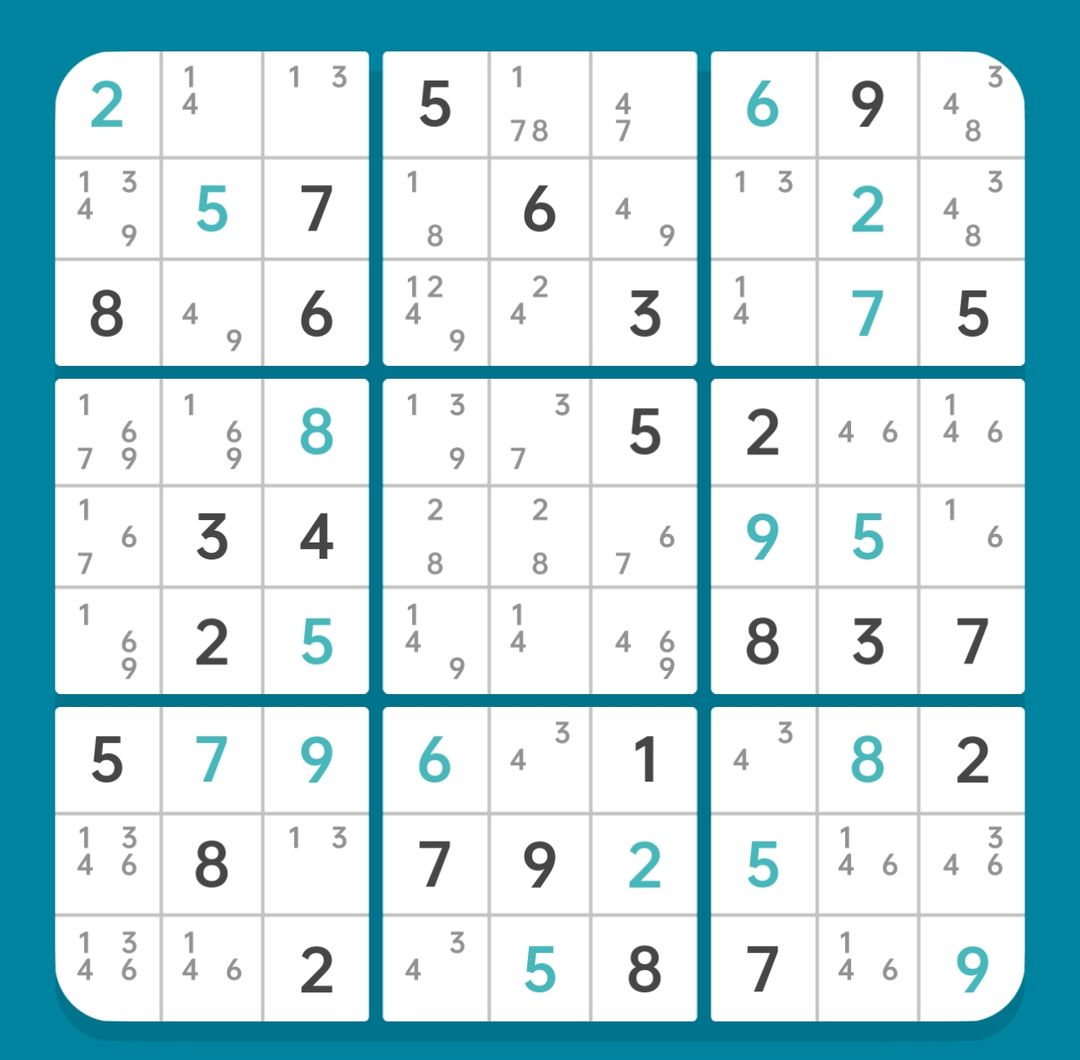
TapTap

图15-2.3.3

Step 4 刺SDC构造强链

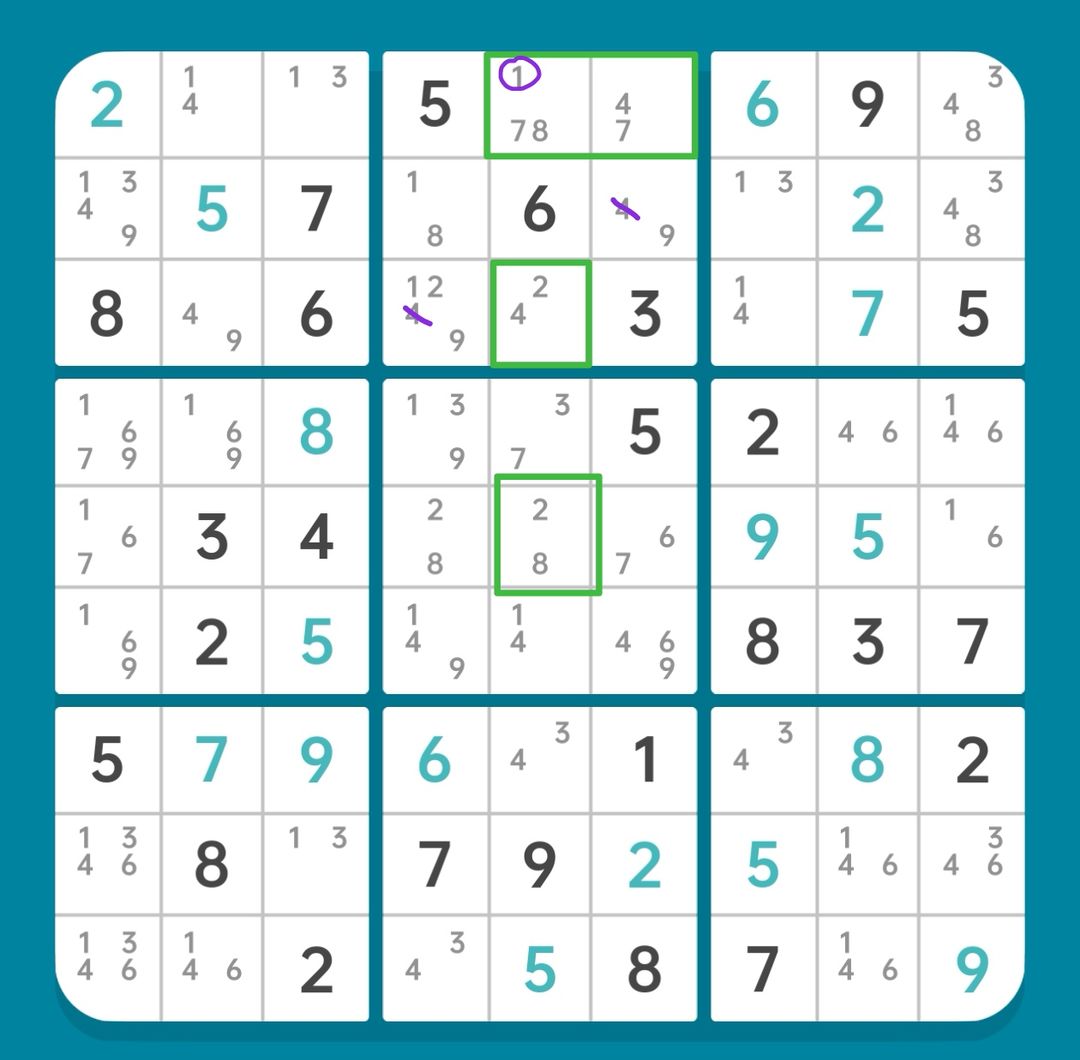
TapTap

图15-2.4.1 刺SDC

这一步我们用另一种方式利用毛刺。注意到，如果r1c5(1)不存在，则绿框四格构成标准SDC，故有如下预备删数：

r2c6(4)，r3c4(4)

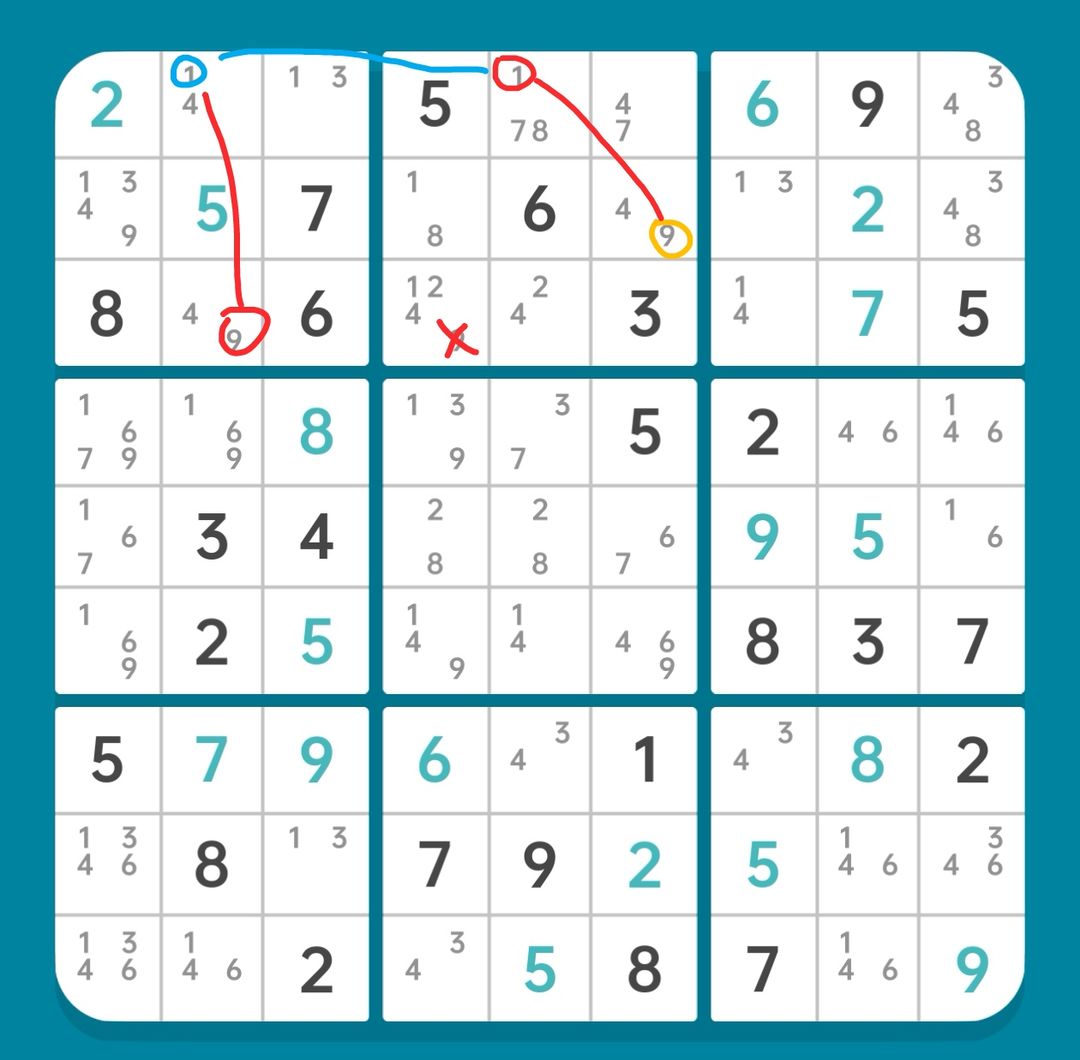
TapTap

图15-2.4.2 刺SDC构造的强链

于是我们发现，如果r1c5(1)不存在，则r2c6=9。故构造强链

r1c5(1)=r2c6(9)

稍作延伸，得链

r2c6(9)=r1c5(1)-r1c2(1)=r3c2(9)

【删数】r3c4(9)

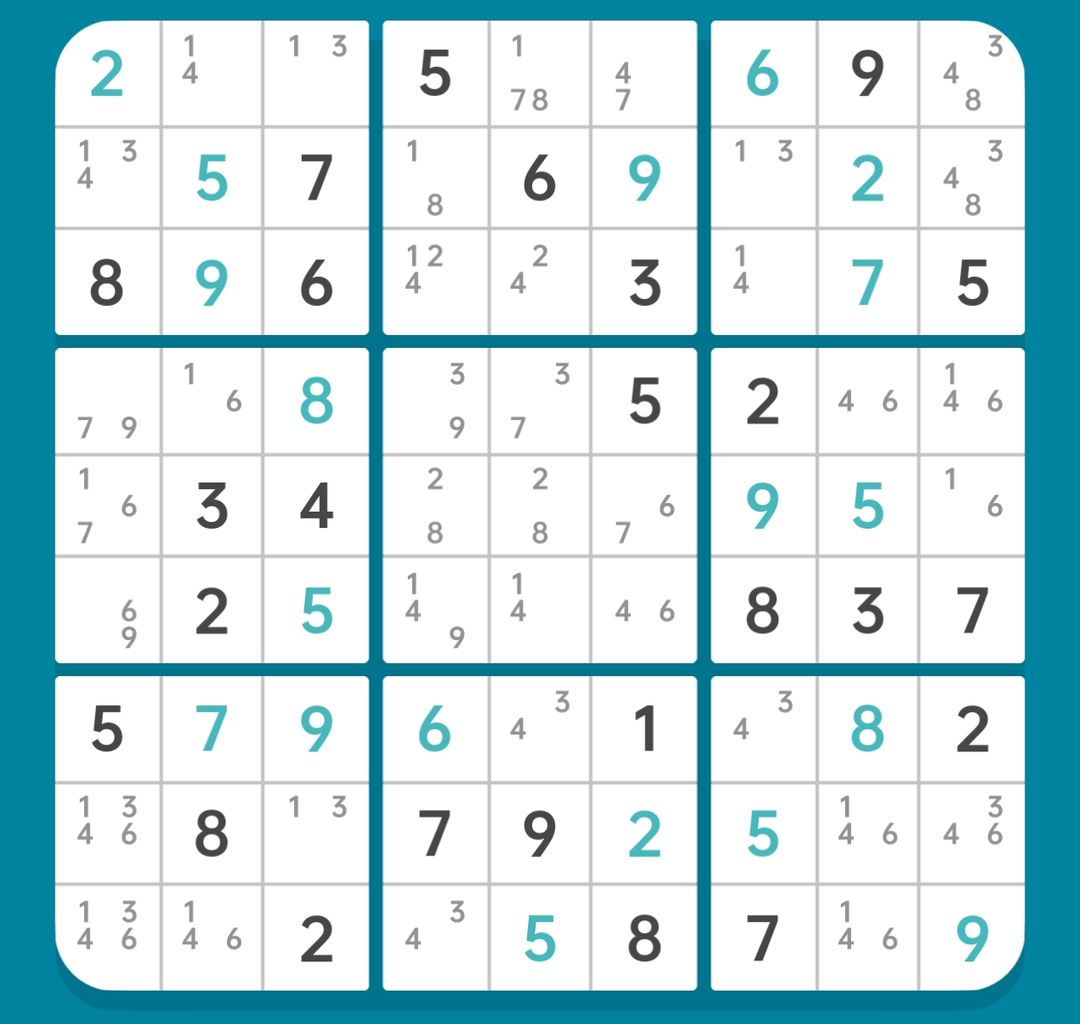
TapTap

图15-2.4.3

Step 5 AIC

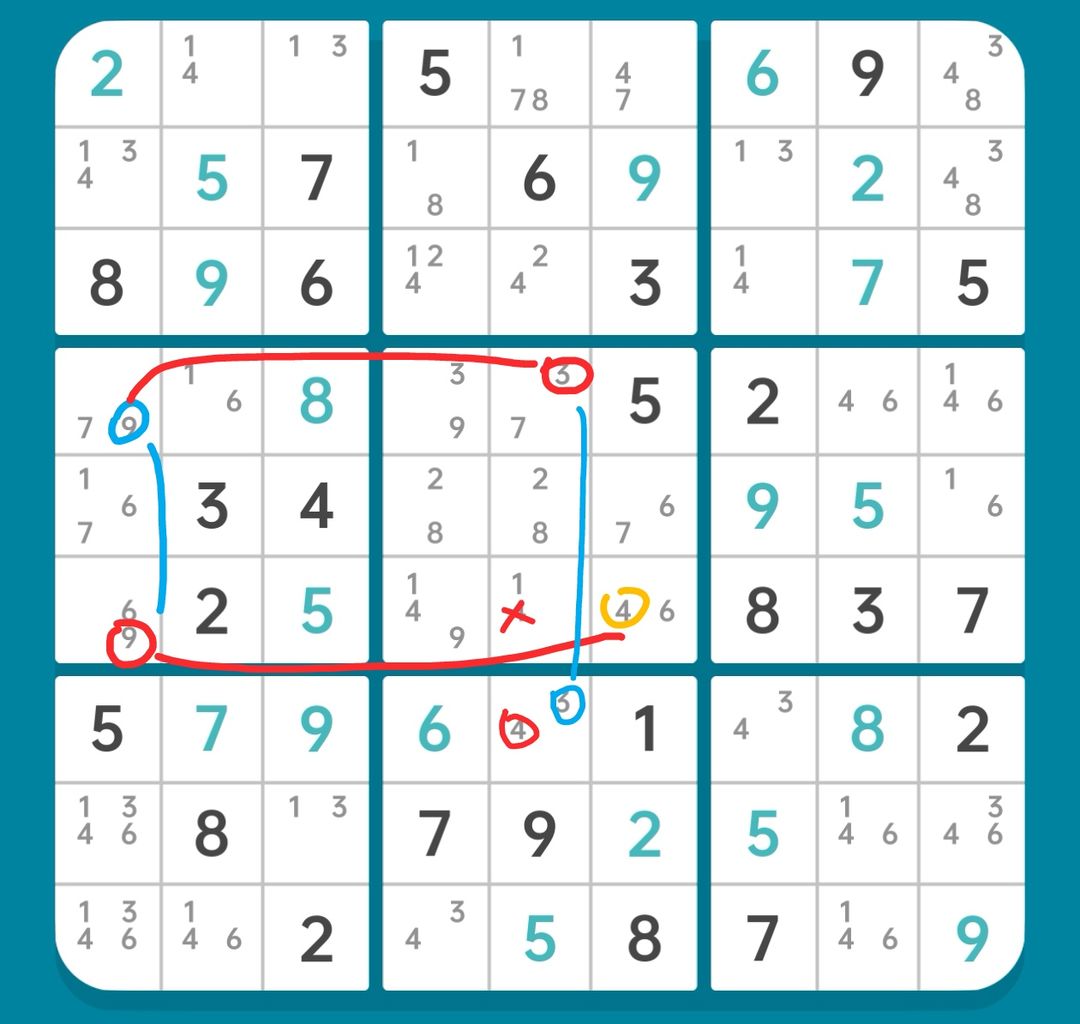
TapTap

图15-2.5.1 AIC

如图15-2.5.1，找到如下链：

r6c6(4)=r6c1(9)-r4c1(9)=r4c5(3)-r7c5(3=4)

【删数】r6c5(4)

TapTap

图15-2.5.2

Step 6 （最后一步）W-Wing构造强链

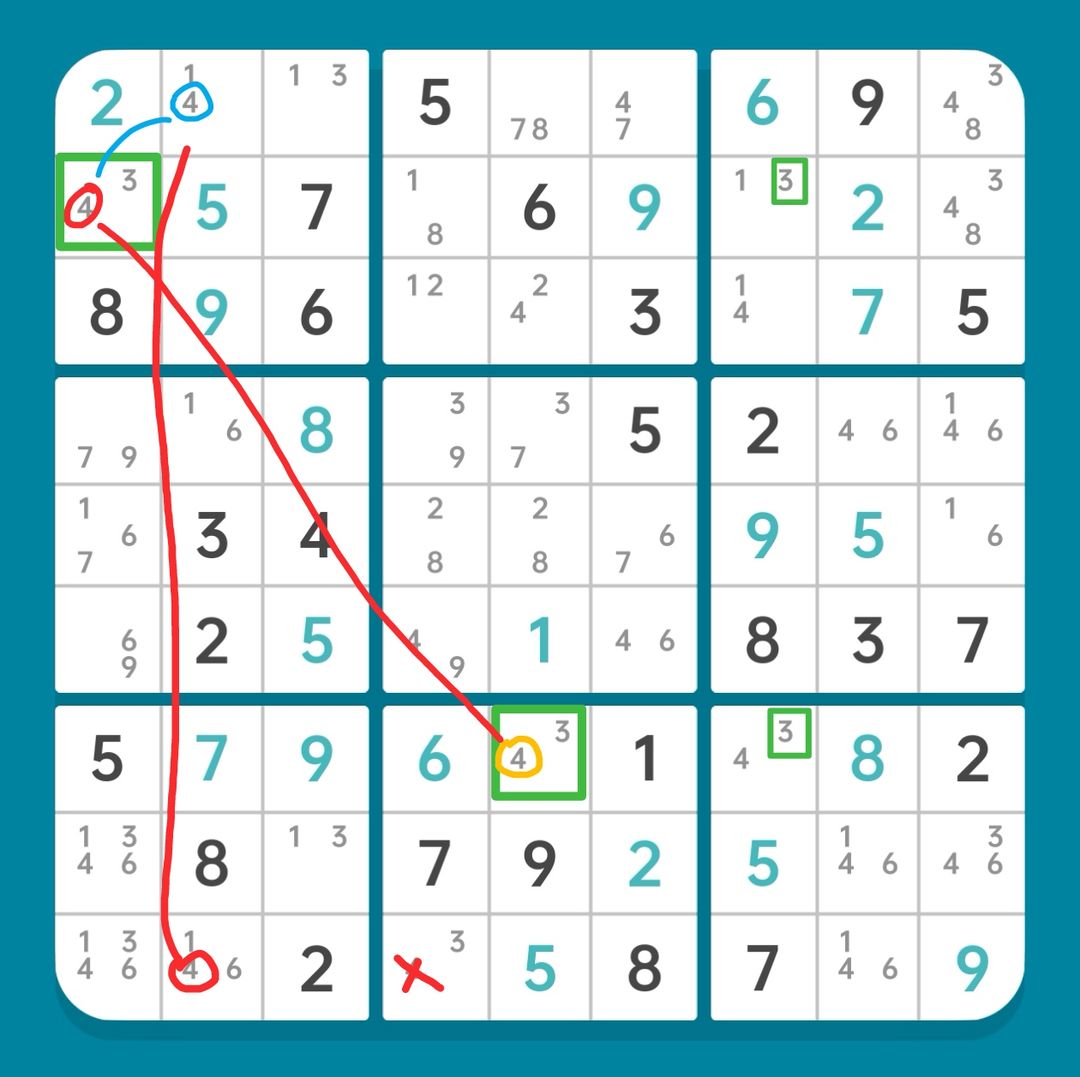
TapTap

图15-2.6.1 W-Wing构造强链

如图15-2.6.1，首先根据绿框得到W-Wing，从而有强关系

r7c5(4)=r2c1(4)

稍作延伸，得链

r7c5(4)=r2c1(4)-r1c2(4)=r9c2(4)

【删数】r9c4(4)

数独清测试

9.2