EH的数独杂谈 #12-1 毛刺初步
2024/12/01153 浏览攻略
前置知识:本系列1-6章,7-1,8-1,8-2,9-1,9-2,10,11-1
(如果没能全部掌握也不要担心,感受本节提供的思路即可)
--------目录--------
一、从鱼鳍到毛刺
二、毛刺的用法&一些约定
1. 毛刺的用法
2. 一些约定
三、毛刺实战
1. 刺数组
2. 刺AIC
3. 刺连续环
四、毛刺与构造的联动
--------------------
欢迎回来!在第11章中,我为大家展示了三大法宝之一——构造,它能帮助我们发掘更深层次的强关系或弱关系。但即使知道了这个思想方法,在实战中依然可能会受到局限:在候选数非常多的时候,你可能很难将链拓展到其他地方去,导致你在构造过程中进行的种种尝试都有可能无功而返。
另一种情况更加令人烦恼:你费尽心力在盘面上试图寻找你所知道的结构,例如XY-wing,链列,连续环,SDC等等,结果却发现总是多出一两个候选数,导致结构无法直接使用。
在过去,这会导致你不得不改弦易辙,去其他地方寻找能用的技巧,或者寻求非常冗长而晦涩的链。但现在,我将为你带来三大法宝之二,它可以从这种窘境中开拓新的路径,将已有的结构的价值发挥到极致——
让我们有请:毛刺。这会是你所接触过的最伟大的思想方法之一。它和数独其他一切技巧联动,而且配合构造和秩理论可以发挥其最大效用。
但是,熟练掌握毛刺需要大量的练习和刻苦的思考。你准备好了吗?
一、从鱼鳍到毛刺
在8-2中,我们已经接触过鳍鱼的一个实例了,详见图12-1.1。
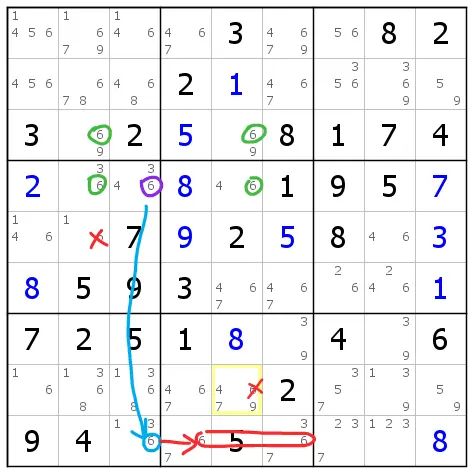
图12-1.1 一个鳍鱼,这里的鳍就是毛刺
图中绿色圈表示一条二链列,r4c3(6)是这条鱼的鳍。如果没有这个鳍,那么绿色圈就能发挥标准二链列的作用,删除c25两列其余的候选数6。现在由于鳍的存在,删数的规模受到了限制。
在这里,结构不仅可以删除r5c2(6),还可以通过将鳍直推的方式,进一步删除r9c46(6)。在这个过程中,我们实际上是在找“鳍为真”和“原标准二链列为真”时的共同结论。
这两段话就共同阐释了毛刺的概念:当原结构由于多出了一些候选数导致其不能直接使用时,这些多出来的候选数称为该结构的毛刺;特别地,如果原结构的部分删数可以被所有的毛刺删除,那么这些删数就一定可以删除。显然在刚才的例子中,这个r4c3(6)就是二链列的毛刺。
像构造一样,读者不必在毛刺的概念上钻牛角尖。
二、毛刺的用法&一些约定
1. 毛刺的用法
根据毛刺的概念,毛刺通常有如下使用方法(本节只需掌握第1条;第2条和第3条我们会在以后的章节介绍):
(1)设刺为真,通过直推删除原结构的删数;
(2)对于准秩零结构(第13章会讲),其毛刺如果推出预备删数(往下看)为真,则形成绽放环(第13章会讲)产生额外删数;
(3)对于准秩零结构,如果毛刺为真可以导致矛盾/无解,或者其删除了所有的预备删数,则毛刺本身可以删除。
2. 一些约定
为了后续的交流方便,现作出如下约定和定义:
(1)当毛刺不存在时,原结构的删数称为『预备删数』。之所以叫预备删数,是因为它们并不能直接删除,需要进行验证。
(2)在笔者的图中,默认以紫圈代表毛刺,紫线代表预备删数;暖色调箭头代表直推(即依次经过一条弱链和一条强链,也就是通过A真推得B真的过程),红色叉叉代表确定的删数。
三、毛刺实战
在讲完必要的概念之后,是时候带你们亲身感受毛刺的威力了。我们将通过三则实例讲解毛刺的第一种用法,但你完全可以将毛刺用于其他地方。
1. 刺数组
如果一个数组里多出了一个候选数,我们以往会将其当做ALS来寻找强弱关系。现在,你可以把多出的候选数当做毛刺进行直推,找到和原数组共同的删数结论。
让我们看看图12-1.2吧。
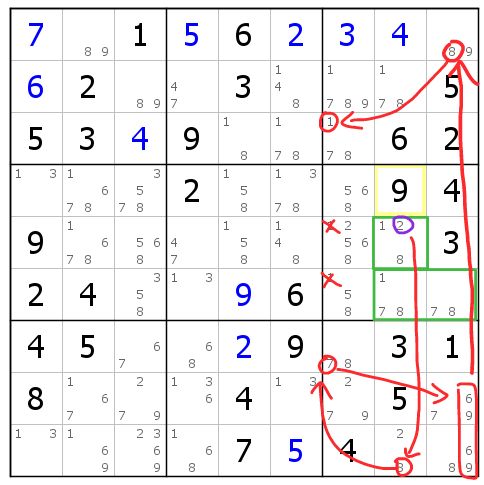
图12-1.2 刺数组一例
六宫的绿框内,如果没有毛刺r5c8(2),则构成178数组,其预备删数如下:r2c8(1),r56c7(1)和r456c7(8)。
现在当毛刺为真时,我们可以按照图上的红色箭头,依次推出r9c8(8),r7c7(7)为真。这样r89c9成为69数组,推出r1c9(8)为真。结合r7c7(7)和r1c9(8),推出r3c7(1)为真。
这个r3c7(1)可以删除r56c7(1),也就是删除数组的预备删数。所以r56c7(1)就是结构的删数。
*部分读者可能会在这里纠结:刚才的过程不就是把r5c8(2)代入吗?这跟粗暴的试数有什么区别?
*实际上,纯粹的试数并不总是正确的,其正确与否在选定要代入的数字之时就已确定,并且直到余盘瓦解或者发现矛盾才能作出定论;但这里毛刺的代入是为了找寻公共结论,通过刺真得到的公共删数,是可以保证一定正确的,并允许玩家立刻将其删除。
2. 刺AIC
如同数组一样,链也可以采取毛刺。具体来讲,如果删去一个候选数能产生一条有结论的链,那么完全可以把这个候选数当做毛刺。
图12-1.3展示了一个刺W-Wing的例子。
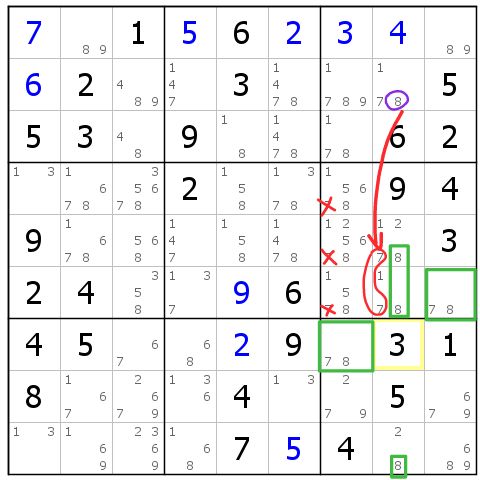
图12-1.3 刺W-Wing一例
我们知道,W-Wing就是一条特殊的链。注意到两个绿框框起来的只含候选数78的格子,以及8列的数字8的排布。要是没有r2c8(8),W-Wing就形成了。
因此以r2c8(8)为刺,则绿框构成W-Wing,得到强关系r7c7(7)=r6c9(7),预备删数如下:r456c7(7),r8c9(7)。
当毛刺为真时,可以直推出r56c8(7)为真,从而删除r456c7(7)。
3. 刺连续环
刺连续环除了直推公共结论以外,还有一些独特的性质,这使得刺连续环比刺AIC更加强大和实用。当然,这并不是现在就需要关心的问题。
图12-1.4是一个刺连续环的例子。
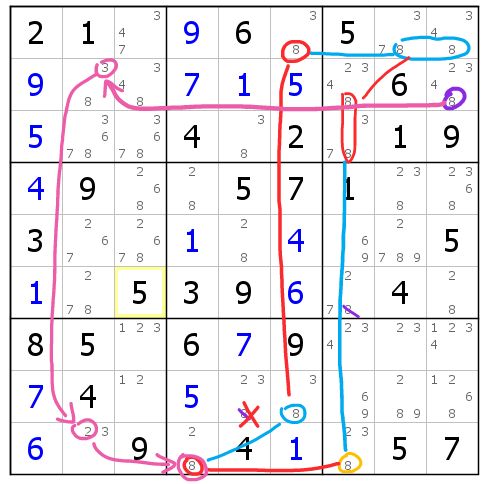
图12-1.4 刺连续环一例
我们暂时忽略所有的粉线。如果你要在这里寻找关于8的单数链,你可能会找到下面的双线风筝:
r1c6(8)=r8c6(8)-r9c4(8)=r9c7(8)
它没有直接的结论。但如果以r2c9(8)为刺,这条链就能进一步延展为连续环:
r1c6(8)=r8c6(8)-r9c4(8)=r9c7(8)-r23c7(8)=r1c89(8)-r1c6(8)
其预备删数有r8c5(8)和r6c7(8)。
现在令刺为真,则沿着粉色箭头,直推出r2c2(3),r9c2(2),r9c4(8)。从而删除r8c5(8)。
如果你看懂了上面的三个例子,你就理解了毛刺的最基础用法。如果你能够完成3-4星的题目,但面对5星题目束手无策,那么现在,你就已经拥有了对抗5星题的法宝。
选择对什么结构使用毛刺,是非常自由的。但想要让你的毛刺一针见血,就需要大量的练习来积累实战经验了。
四、毛刺与构造的联动
在11-1中,我们讲述了基于AIC+和规避非法结构的构造。有了毛刺之后,构造的方法就又多了一种:
如果原结构成立,其预备删数全部删除时可以出数,则毛刺与这些出数成强关系。
有些抽象?没关系,我们来看看图12-1.5的例子。
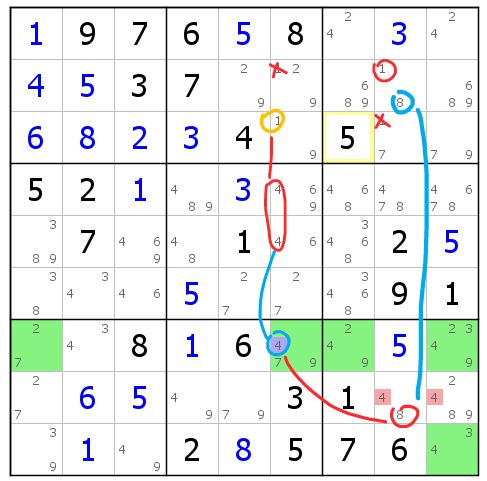
图12-1.5 使用毛刺构造强链
首先注意涂绿的五格,以紫色的r7c6(4)为毛刺,如果去掉它,则这五格形成SDC,其预备删数为r8c89(4),从而出数r8c8=8。
这时我们发现,去掉r7c6(4)能推出r8c8(8),这不就是强链的定义吗?将这个强链稍作拓展,得链
r3c6(1)=r45c6(4)-r7c6(4)=r8c8(8)-r2c8(8=1)
产生删数r2c6(1)和r3c8(1),余盘瓦解。
当然,这个结论直接用链也能得到,这里只是以此说明毛刺构造强链的思路。万一你需要它呢?
小结:
(1)当原结构由于多出了一些候选数导致其不能直接使用时,这些多出来的候选数称为该结构的毛刺;特别地,如果原结构的部分删数可以被所有的毛刺删除,那么这些删数就一定可以删除。这是毛刺的最基本逻辑。
(2)可以使用毛刺来构造强链:若原结构成立时可以出数,则毛刺与这些出数成强关系。



