EH的数独杂谈#8-2 鳍鱼,退化鱼与孪生鱼
修改于2024/11/29158 浏览攻略
--------目录--------
一、鳍鱼的概念与删数逻辑
二、一鳍多用
三、退化鱼
四、孪生鱼
--------------------
前一节的内容:
在8-1中,我们讲解了标准鱼(或称链列)的概念和使用方法。尽管这是个很优雅的结构,但实战中并不是总能遇到。有时候结构会比标准鱼多出一两个数字;如果把它们删掉,剩下的结构就是标准鱼。我们称这样的数字为『鳍』。
一、鳍鱼的概念与删数逻辑
话不多说,直接上例子。下图是你游五星第1关,如果你熟练掌握了四大基本技巧(摒除,唯余,数组,区块),你会做到下面的盘面:

图8-2.1 一个鳍二链列的实例
我们关注4列和9列的候选数4,它们分布在三行(r469)上。这并不符合标准鱼的定义;但如果删除r6c9(4),那么剩下的四个4就构成了标准二链列。因此在这里,r6c9(4)就是这条鱼的鳍,这个结构称为鳍二链列。
现在看看鳍鱼的删数逻辑。我们按照鳍是否存在来进行讨论:
(1)r6c9(4)不存在,则r49c49(4)构成二链列,其定义域是c49两列,删数域是r49两行。这两行除了绿圈之外的候选数4均可删除。
(2)r6c9=4,则可以立即删除r4c7(4)。
根据上面的分析,我们发现:不管鳍存不存在,r4c7(4)都可以删除。这就是鳍鱼相对于标准鱼的一些麻烦之处:我们需要对鳍是否存在作分类讨论,寻找公共的删数结论;而且它的删数往往不如标准鱼那么多。但相对于标准鱼,鳍鱼才是更为常见的结构,用好鳍鱼会对解题大有帮助。
现在总结一下鳍鱼的使用方法:
(1)像标准鱼一样,确定一批定义域。如果它是鳍鱼,其删数域会比定义域多一些;
(2)确定鳍的位置,使得去掉这个(些)鳍之后,剩余部分构成标准鱼;
(3)则鳍鱼的删数是标准鱼删数和鳍为真时删数的『交集』(也就是公共结论)。一般来说,这样的删数位于鳍所在的宫内。
如果一时没有理解,可以回看图8-2.1的例子进行对照。如果你理解了,那么就可以自行分析图8-2.2的鳍三链列了。
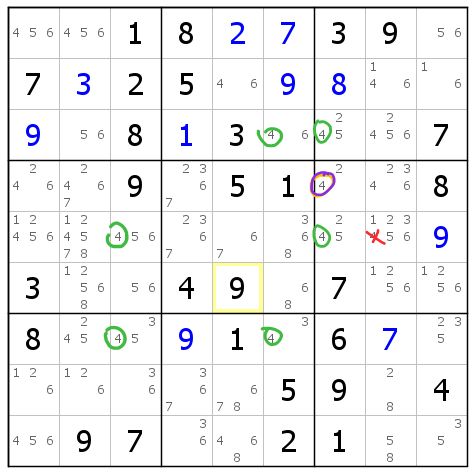
图8-2.2 鳍三链列
二、一鳍多用
尽管鳍所在的宫内往往会出现删数,但删数不一定只出现在鳍所在的宫内。鳍鱼的删数是标准鱼删数和鳍为真时删数的『交集』,所以不管是“鳍为真”这件事本身,还是由“鳍为真”推导出的二级结论,只要和标准鱼删数有交集,就都可以使用。
用一个例子来详细讲述这一点。
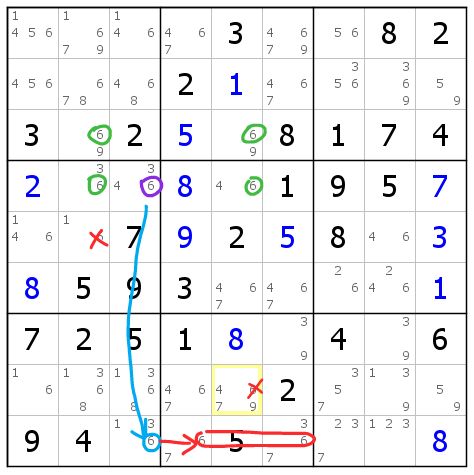
图8-2.3 一鳍多用
首先根据上一部分的内容,删除r5c2(6)是很好理解的。
然后,当鳍r4c3(6)为真时,我们推出r9c3(6)为假,从而r9c46(6)区块为真。这时我们注意到,无论是原来的标准鱼,还是r9c46(6)区块为真,都可以删除r8c5(6)。因此r8c5(6)也是鳍鱼的删数。
由此我们知道,鳍鱼的鳍其实是相当灵活的。在第12章中我们将会说明,鳍是毛刺的一个特例,它具备毛刺的所有性质。
三、退化鱼
鳍鱼的鳍产生于标准鱼之外。那如果标准鱼本身就是残缺的呢?在上一节中我们已经知道,残缺并不意味着鱼本身不成立。因此从残缺的鱼生长出鱼鳍也是合乎逻辑的,我们称这样的鳍鱼为退化鱼(Sashimi Fish)。
尽管逻辑一样,但退化鱼相比一般的鳍鱼会更灵活一些。先来看一个退化二链列的实例:
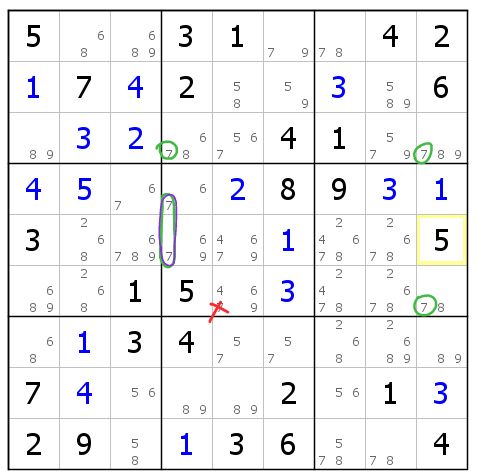
图8-2.4 退化二链列
一些熟悉双强链的读者大概注意到这是个摩天楼了。但这次,我们从鱼的角度来分析。
首先注意到c49两列上7的位置。然后我们将紫圈,也就是r45c4(7)当做鳍。如果删掉鳍,剩下的三个绿圈就构成了标准鱼。
啊嘞?这样的话不就直接出数了吗?是的,但这依然符合标准鱼的定义:在c49两列上,这三个7还是只能分布在r36两行。所以标准鱼的删数是以下位置的7:r3c58,r6c578。
而当鳍为真的时候,可以直接删除r6c5的7。故r6c5(7)为结构删数。
接下来是退化三链列,这个例子就更有趣了。
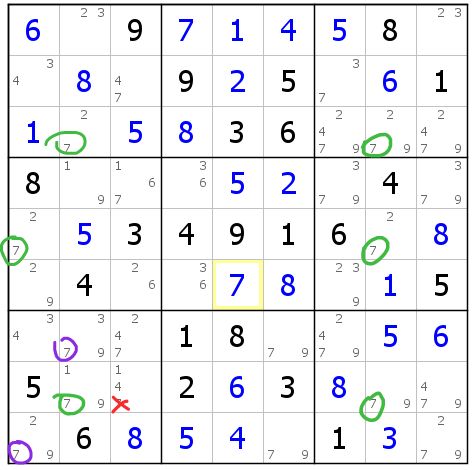
图8-2.5 退化三链列
是的!鳍可以不只有一个!但存在不止一个鳍的时候,我们需要寻找每一个鳍为真时的删数,以及原标准鱼删数的共同结论。只用一个鳍是不够的。
我们关注c128三列的7。如果把紫圈的两个7都去掉,那绿圈的这些7就是标准三链列。所以紫圈的两个7都是鳍。
然后,当鳍为真时,它们和三链列的共同删数是r8c3(7)。
四、孪生鱼
当鳍鱼满足一定条件的时候,你可以从一条鱼里按两种不同的方案找到两套不同的鳍,甚至这两套鳍都分别有删数。这种鳍鱼称为孪生鱼(Siamese Fish)。
如果不懂的话,看看下面的孪生三链列。你会如何去找到它的鳍呢?
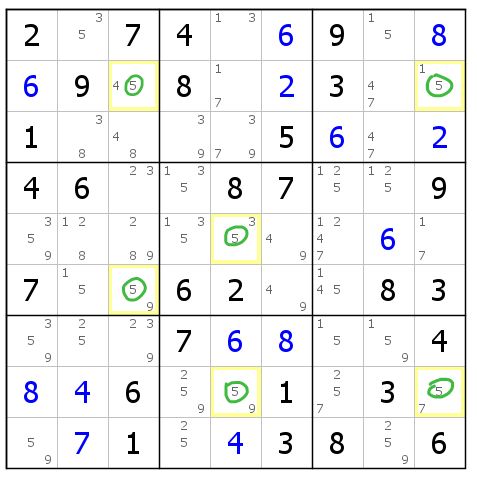
图8-2.6.1 孪生三链列(未画出鳍)
注意到它的定义域是c359三列,而这些5分布在四行内。你或许很容易就想到将r6c3(5)看作鳍,详见图8-2.6.2。
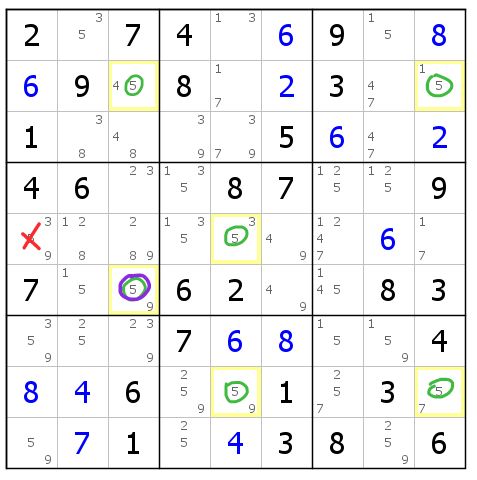
图8-2.6.2 孪生三链列的一种解释方式
但其实也可以采用图8-2.6.3的方式,把r5c5(5)当做鳍。它还是鳍三链列,只不过按照这种方式,你就看不到刚才的删数了。
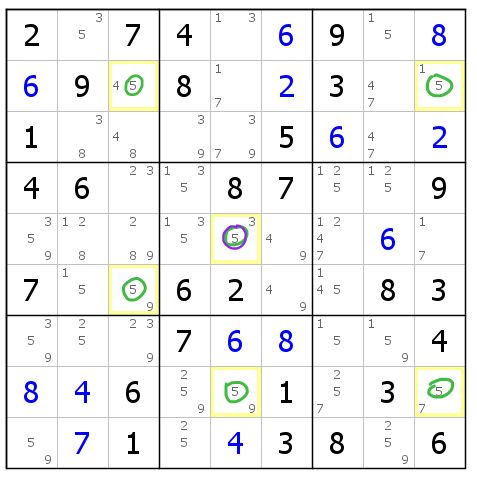
图8-2.6.3 孪生三链列的另一种解释方式
这就是孪生鱼的有趣之处,根据不同的观察方法和对鳍的不同选择,可以得到不同的结论。
有时候,两种观察角度能分别产生不同的删数。你能找到下面这个孪生三链列的全部删数吗?

图8-2.7 另一个孪生三链列(未画出鳍)
-注:根据秩理论的内容,可以直接构造强链r4c4(1)=r8c6(1)。我们会在第13章进行介绍。
小结:
(1)鳍鱼相对于标准鱼多出来一些数字,这些数字称之为鳍。鳍鱼的删数是标准鱼删数和鳍为真时删数的交集。
(2)由鳍为真推出的二级结论,在鳍鱼中仍然可以使用。
(3)鳍可以不止一个。但这种情况下应该找每一个鳍为真时的删数,以及原标准鱼删数的共同结论,不能只使用一部分鳍而忽视另一部分。
(4)退化鱼和孪生鱼是鳍鱼的特例。退化鱼的分析方法和一般的鳍鱼一致;但孪生鱼可能会因为鳍的选择方式不同而产生不同的删数,使用时需多加注意。



