EH的数独杂谈#9-2 SDC的演化视角
修改于2024/11/29116 浏览攻略
--------目录--------
一、再谈SDC——为什么能融合?
二、演化视角下的自噬SDC分析
三、多段SDC初探
1. 三段SDC
2. 四段SDC
--------------------
前一节的链接:
欢迎回来!这句不仅是对看到这篇杂谈的大家说的,也是对我自己说的。时隔一年,EH带着更新过的知识库回来啦~
在9-1中,我们初步介绍了SDC(融合待定数组)的概念。但那一节对SDC的观察方法非常令人绝望:不仅使用了大量繁复的数学符号,而且完全没有表达出SDC的精髓。尽管足够准确,却令人望而却步(如果你真的看懂了9-1我在说什么,你恐怕就不需要这篇教程了)。
在本质上,SDC是在逻辑上可以分离为多个数组并且分开使用的候选数结构。因此,SDC不应是从天上掉下来的一大块结构,而是存在一个从数组『演化』到SDC的过程。
综上,这一节的目的就是讲清楚SDC的演化,并按照这一底层逻辑,帮助大家独立推导出更加复杂的SDC结构。
一、再谈SDC——为什么能融合?
SDC往往起源于一个『差点形成数组』的区域。让我们重新观察上一节的第一个实例。
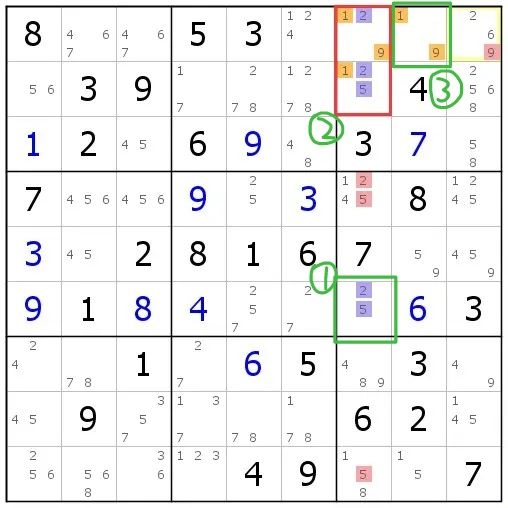
图9-2.1 SDC的演化视角
显然,结构涉及的四格,在7列和3宫里都没有直接构成数组,仅仅是『差点形成数组』。但我们可以直接讨论红框中的填数情况,并最终得到『框内紫色数字(25)和橙色数字(19)分别只能填一个,不能多也不能少』的结论。
现在我们把视角转换一下,从标有①的绿框开始分析:
①r6c7有一格(①)有候选数25,7列上已经有了一个25;
②那么红框里的候选数25,最多能填入一个(否则7列的25就要填在三格里,这违背了数独规则),从而红框剩下的候选数19至少能填入一个。
③这时注意到三宫内有一格(③)只包含候选数19,它为三宫提供了一个19。那么红框的候选数19最多能填入一个(否则3宫的19就要填在3格里,同样违背数独规则)。
这里就是结论产生的地方。既然红框里的19至少填一个,又最多能填一个,那红框就有且只有一格(A)能填19,从而红框内另一格(B)能填25。于是在红框所占据的区域内:
·3宫里,A格和③号格形成19数组,3宫里结构之外的候选数19均可删除;
·7列上,B格和①号格形成25数组,7列上结构之外的候选数25均可删除。
分析结束。上一节告诉我们,SDC可以分成两个数组来使用;而这一节则反过来,它启发我们,在满足一定条件时,两个数组可以构成SDC。这种通过数组演化出SDC的观察方法,更加符合我们对于新知识的认知,在实战中也更容易操作。
比较有趣的是,这种分析方法是不分方向的。换言之,你完全可以从③格分析到红框,再分析到①格,可以得到和刚才同样的结论。为何不试试呢?
二、演化视角下的自噬SDC分析
有了这种演化的分析思路,分析一般的SDC对你们而言已经不在话下了。但对于自噬类型的SDC,还要多把握一点点细节。
我们已经学过,结构删数反过来删去了结构某些组分甚至结构本身的现象,就称作自噬。如同图9-2.2的例子一样,r9c5(4)不仅是SDC结构的一部分,而且是这个结构的删数。
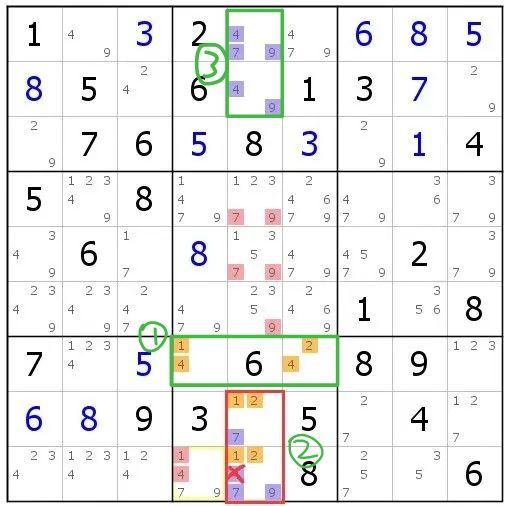
图9-2.2 自噬SDC
我们用演化视角来看看这个结构吧:
①在8宫内,①所代表的两格可以填入124;
②于是红框的124至多填一个,从而红框的79至少填1个;
③视角转到5列,③所代表的两格里有两个479,从而红框的79至多填1个;
④结合上述分析,我们知道红框内124和79各填一个,SDC成立。
仅仅用上面的分析过程似乎不足以直接删除r9c5(4),但如果结合反向视角来看:
①在5列上,③所代表的两格可以填入479;
②于是红框的479至多填一个,从而红框的12至少填1个;
③视角转到8宫,①所代表的两格里有两个124,从而红框的12至多填一个;
④结合上述分析,我们知道红框内12和479各填一个,SDC成立。
两种视角显然都正确,那么红框的填数方式应同时满足两种视角下的条件,也就是:
(A)124和79各填一个;
(B)12和479各填一个。
如果红框可以填4,那么根据(A),另一格应填79;但根据(B),另一格就只能填12。不难发现,这两种情况水火不容,不可能同时成立。这表明原假设错误,故红框内不能填4。
实际上,你也可以只用正向视角就排除红框内的4。只要再多考虑一下就可以啦!
三、多段SDC初探
实际上,SDC可以不局限于一行一宫(或一列一宫)。巧用这种演化视角,我们可以发现更大规模的SDC,我们称之为多段SDC。多段SDC在实战中较为罕见,但搞清楚其分析过程对后续学习或许会有好处。
多说定义无益,直接呈上题目。
1. 三段SDC
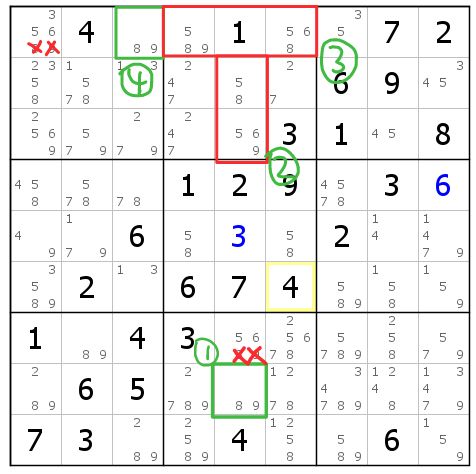
图9-2.3 三段SDC
这个例子就比之前遇到过的所有SDC都更有趣。用演化视角来分析一下:
①在5列上,r8c5已有一个89;
②则红框②内89至多填一个,56至少填一个;
③则红框③内56至多填一个,89至少填一个;
④在1行上,r1c3已有一个89。于是红框③内89恰好填一个,56恰好填一个;红框②内56恰好填一个,89恰好填一个。
这样,该三段SDC结构就产生了5列的89,2宫的56,1行的89这三个数组,分别产生删数。
由此可见,三段SDC和最基本的SDC相比,虽然多了一个红框,核心逻辑却完全一致。
2. 四段SDC
这个例子就留给各位读者自行思考吧!相信有了前文的讲解,你一定能找到所有的删数。
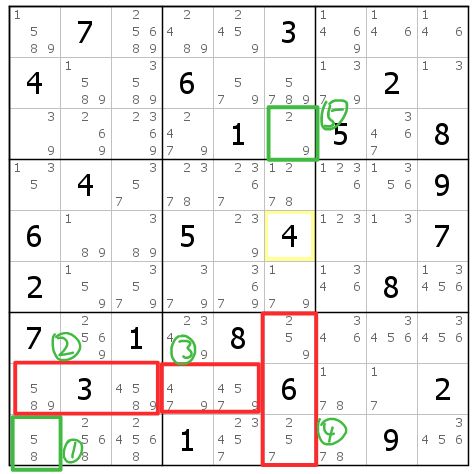
图9-2.4 四段SDC
小结:
SDC往往起源于一个『差点形成数组』的区域,并由数组演化而来。使用演化视角可以分析一个地方是否能形成SDC,并确定该SDC的删数。



