给出具有普遍性的解法思路
修改于2020/10/04351 浏览攻略
第一次发帖,遣词造句上有所欠缺,如有无法理解之处请及时留言,我会尽量用简单的话进行解释。希望大家多多包涵,也希望通过这个帖子抛砖引玉。
我不玩魔方,看到有网友在智商吧推荐这个游戏,于是就下载下来玩玩看。
我建议你们先玩玩下面这个游戏。这个游戏是多年前还在读书时一朋友推荐给我的,朋友想让我帮他解开这个谜题。
好吧,确实不容易,我花了大概两个月的时间才搞定全部的type。这期间脑子里诞生了很多有意思的思路,这些思路用来解决相似的问题是很有用的。可能这些思路对于你们这些魔方玩家来说显得繁琐甚至笨拙,请见谅,毕竟我是在没接触过任何专业知识的情况下独立解决的。
5条重要的思路:
1、type选择3×3normal:在复原前两行后,第三行会有部分方块位置不对,多次尝试后成功复原第三行,这是最原始的试错法。接下来反复restart游戏后发现这样一个事实,最后一行位置的排列组合情形是有限的,这意味着多次游戏中必然遇上相同的情形,例如两次都遇上最后一行左边两个块的位置需要调换。这时可以借鉴之前的还原的经验,采用相同的还原步骤就能解决问题。

2、type选择3×3orientable:反复尝试后发现这样一个事实,位置和方向难以同时复原。退而求其次,那么就先复原位置,再复原方向好了。方向如何复原呢?结合第一条,位置复原后打乱再复原位置,在相同位置上的数字的方向不一定相同,利用这些改变方向的步骤就可以对特定位置上的方向进行还原啦。

3、type选择4×4rotating3×3blocks:和3×3normal相比,有一个重要的不同之处,3×3normal可以只调换一次数字的位置,但是3×3blocks至少要调换两次数字的位置,不可能出现只调换一次位置的情形。关于这点我想了大半月才明白,可以详细解释,这里就不细说了。说一下判定方法好了,2×2block旋转90°、270°时,调换的位置的数量为奇数(调换了三次),旋转180°时,调换的位置的数量为偶数(调换了两次),所以只要调换的数量为奇数,就可能出现最小调换一次的情形,而调换数为偶数,最小调换数只能是两次。3×3block除去中心不动的点可以看作是两个2×2block的结合体,所以无论转什么角度都必然调换偶数次。
4、type选择4×4rotating3×3blocks:与3×3normal还有一点不同,3×3normal的最后一行变化数量极为有限,意味着只需要少量有用的步骤就能完全复原。而3×3blocks不行,最后两行变化数量实在太多,难以用几条的有用步骤复原。为此,我又苦思冥想了很久得到一条行得通的思路:以不变应万变。把需要调换位置的数字移动到已经得到的有用的步骤的位置上,作为交换平台,运用步骤调换完毕后逆着先前的移动顺序倒回去,这样一来就成功交换了特定位置上的数字。

5、type选择6×6rotating4×4blocks:与rotating3×3blocks类似,最小调换数是二,用第三条的判定方法就能判定,不多说了。难点在于这次连有用的调换步骤都难以直接得到,变化数量真的是相当恐怖,想要两次调换的步骤根本无法试出来。我原本想要两对调换的数字,因为这样就能根据第四条调换任意位置上的数字,发现调换完一对数字的位置后存在其他复杂的调换情形。在这个问题上卡了很久后终于在快要疯掉前萌生一个想法,通过适当地重复调换步骤来消除我不需要的调换位置,只留下我需要的调换位置。例如:我需要调换12和34,结果除了12和34还出现了567这个三个数字间的两两调换,通过3次重复把567两两调换给消除了,只留下12调换和34调换。注意,这个方法只能在调换数奇偶不同时才能使用,例如在12调换、34调换、5678调换这个情况下,由于调换数都是奇数,所以无法通过重复消除5678调换,重复四次会把12、34以及5678调换全部消除,此时只能重新尝试。其他缺点也很明显,由于不断重复,所以完成步数极多。
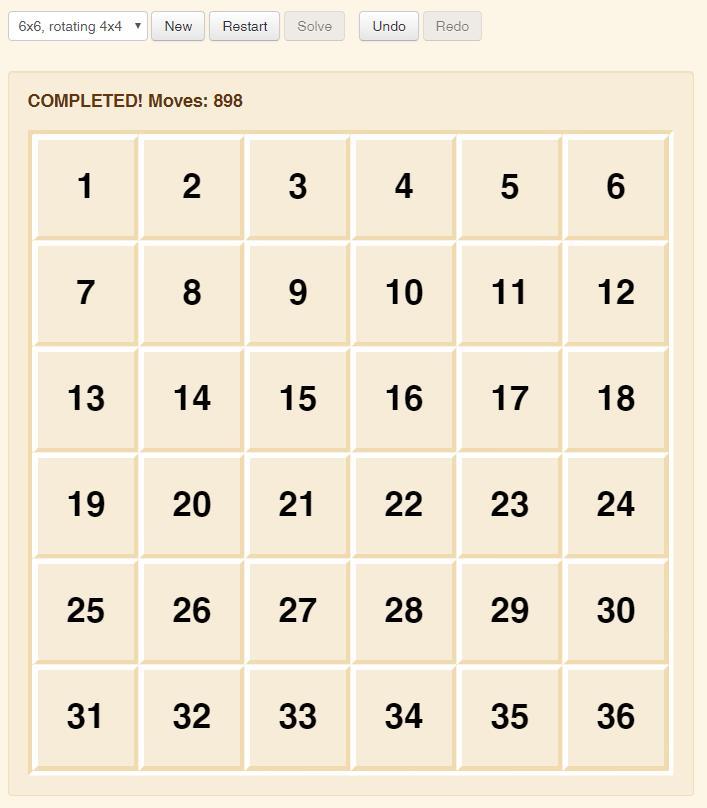
好了,该讲的思路都讲过了,现在来运用屠龙术,我们来看二维魔方,我挑两个具有代表性的关卡来讲,以第二关和第十三关为例。
先来讲第二关,个人觉得难度一般。
与上面所讲的有所不同,第二关我们可以把图形划分成几部分来看,把形状相同的块看作是一份,花瓣形是一份,曲三角形是一份,先复原其中一种形状再复原另一种形状。此外,第二关中色块还具有模糊性,不需要精准复原位置,因此带来了不少便利。
我们先来复原花瓣形。如图,先把左边三个花瓣形复原。具体还原步骤不细说了,没什么技术含量,如果这都不行就别玩了赶紧卸载。
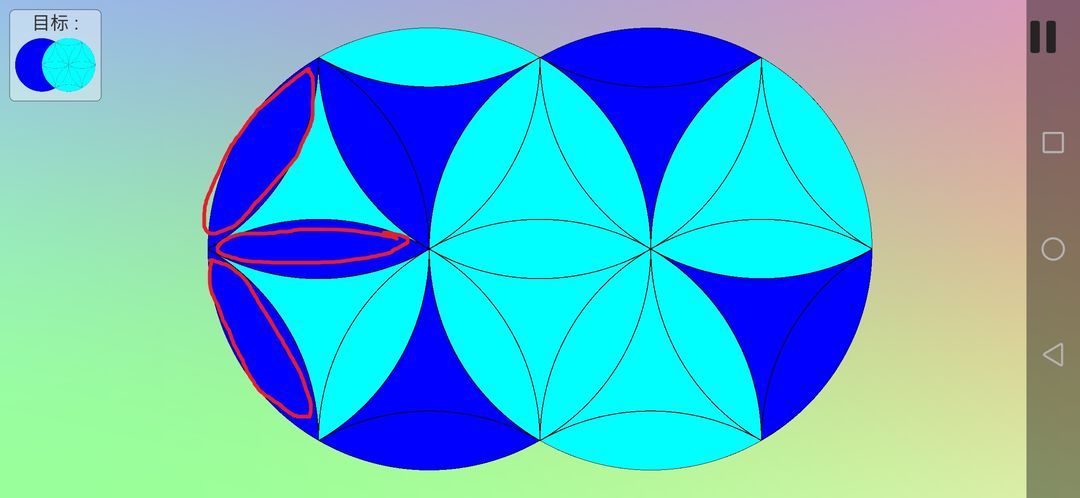
接着把下边两个花瓣形复原(也可以先复原上边的花瓣形)。
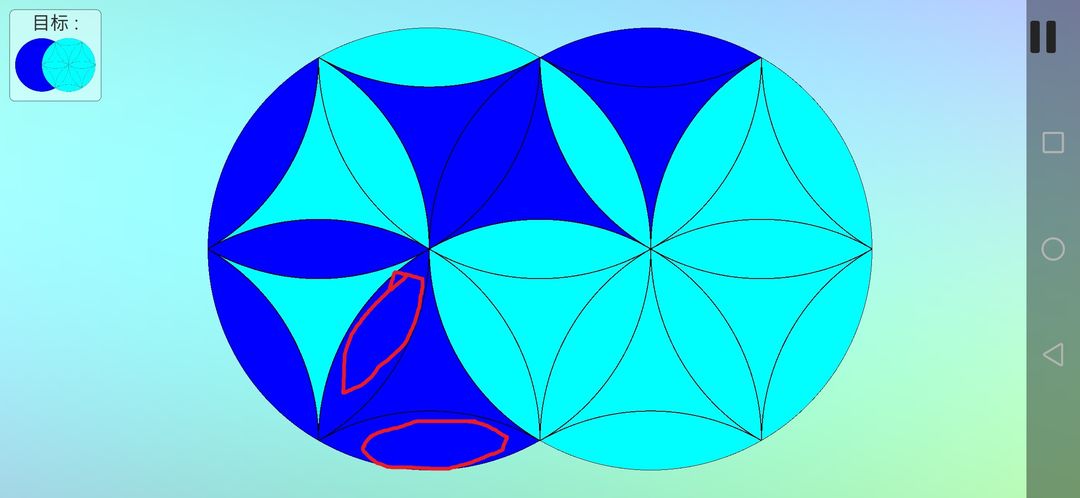
同样,把上边两个花瓣复原。
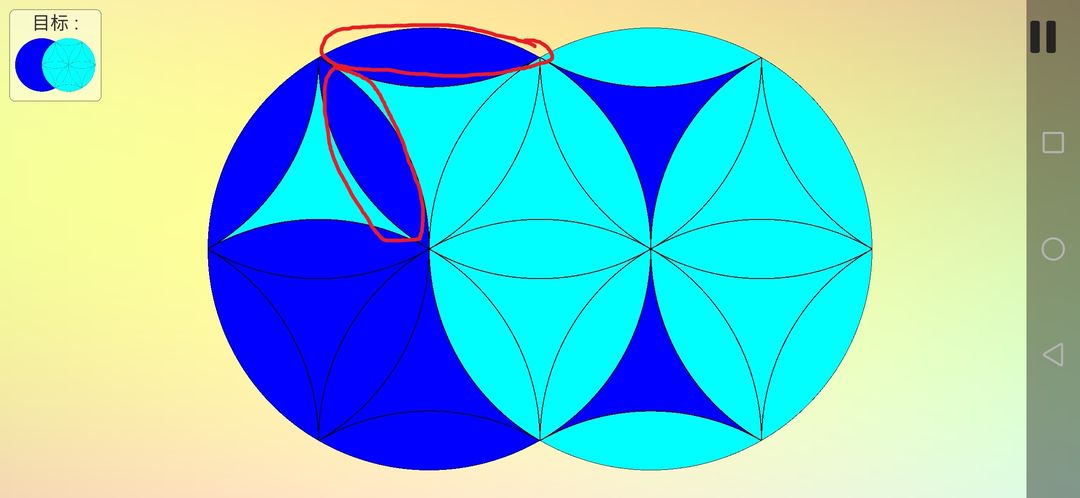
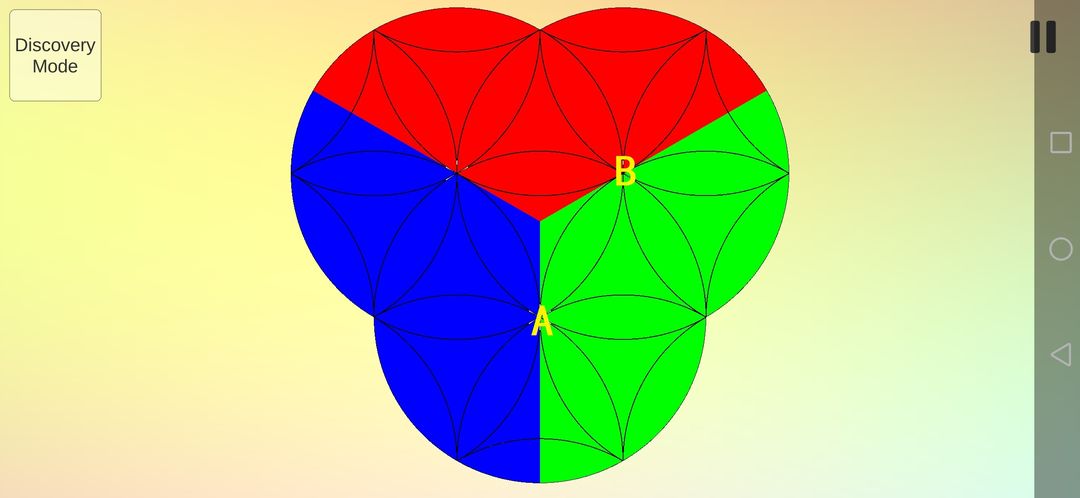
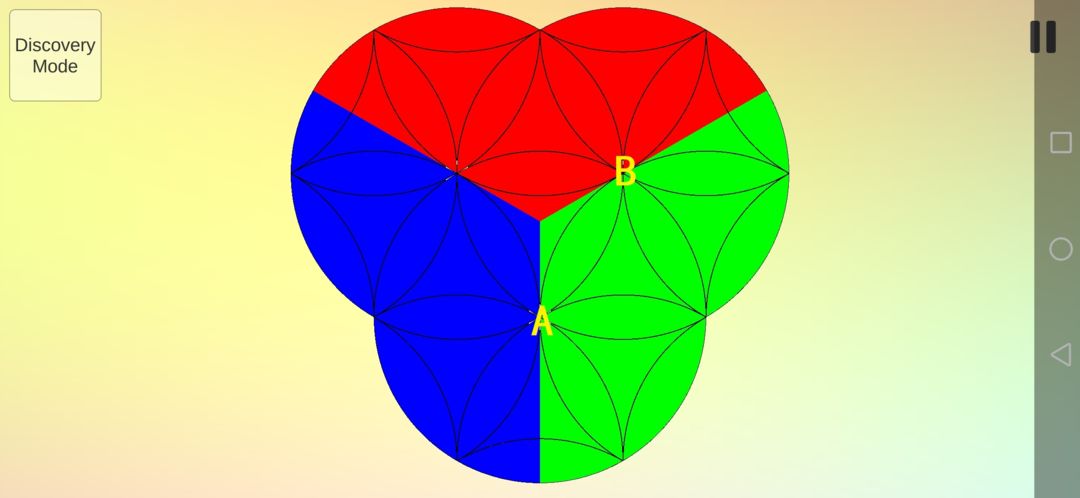
至此,花瓣全部得到复原,现在需要复原曲三角形。为了分析具体的运动,还是要先给每个色块标上数字,并且设左边的旋转中心为A,右边的旋转中心为B。
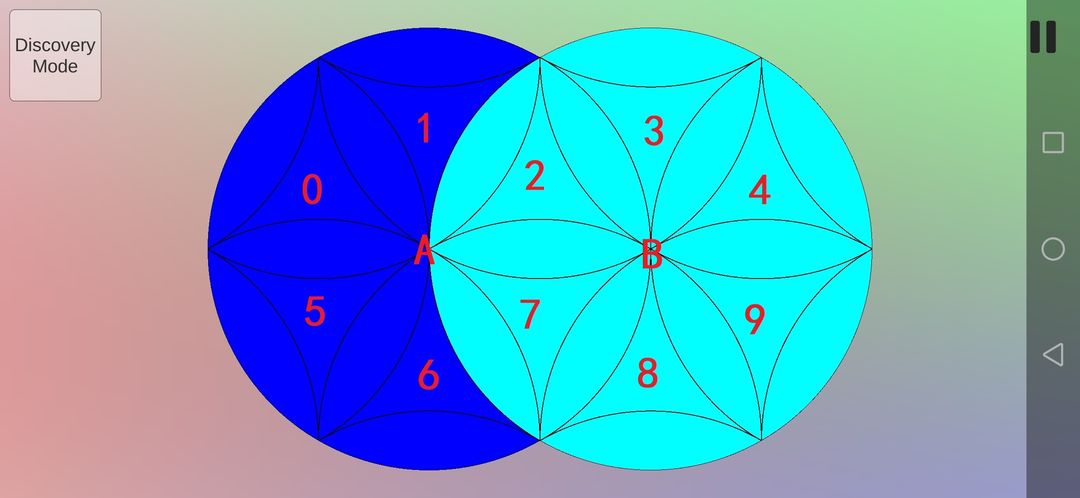
运用第一条、第四条和第五条重要思路,采用最简单的8(A逆B逆),得到下图。具体含义是:A逆时针旋转最小单位60°,B逆时针旋转最小单位60°,重复上述步骤8次,即完成了16次旋转,之后不再赘述。可以看到,除了7以外其他曲三角形都进行了顺时针旋转并且花瓣形看起来没有变化(如果给花瓣进行标识,其实是有变化的,是在同色花瓣间调换位置)。如果你问问这个调换步骤如何得到的,我只能说是试出来的。
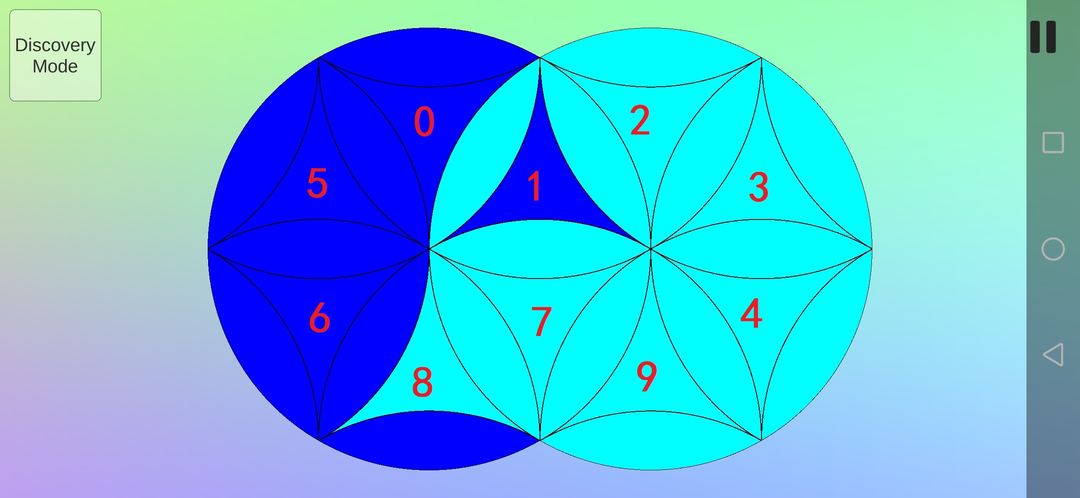
运用这个调换步骤很容易就复原了曲三角形色块。
第十三关就比较有技术含量了,复杂性比较高,具有典型代表,五条重要思路都得到了应用。相比第二关,部分色块的位置需要精准复原,方向也需要复原,花瓣形最小调换次数是2次,曲三角形最小调换次数是1次。第十四关也是典型例子,需要精准还原位置,不需要方向复原,篇幅关系,这里不讨论第十四关。
好了,废话不多说,开始吧。初始状态如图。
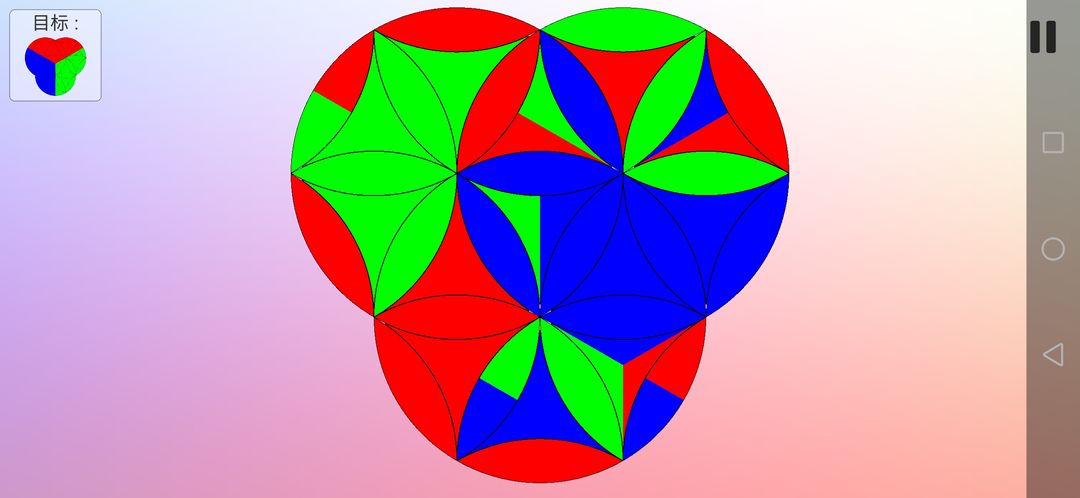
同样先复原花瓣形,我们可选择左上角三分之一圆。注意其中那个有双色的花瓣形的位置和方向变化情况,需提前调整好方向。
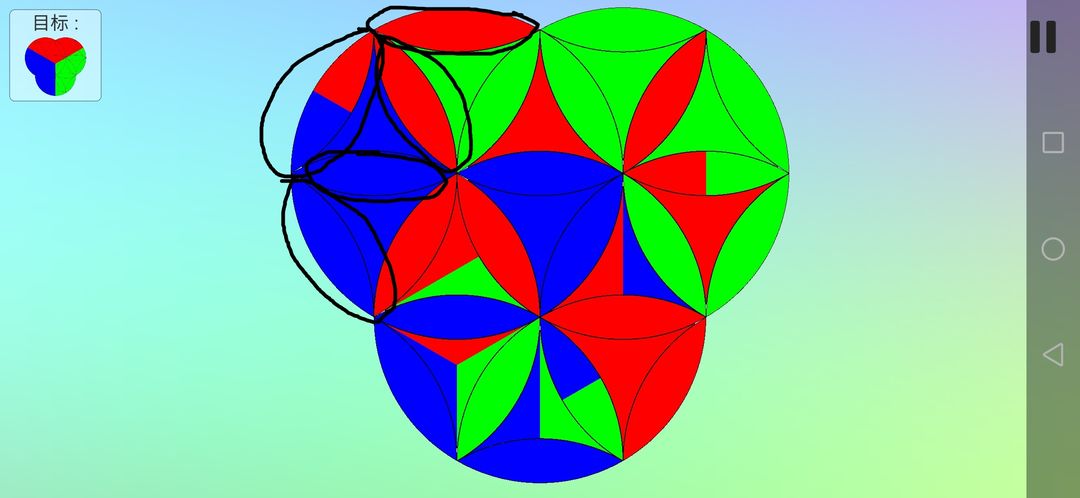
用8(A逆B逆)复原曲三角形,同样需要注意其中那个双色的曲三角形的位置和方向变化情况,提前调整好方向。这样一来,左上角三分之一圆已经复原好了,只需复原另外两个圆。

现在来复原下边那个圆的花瓣形,这次只需注意双色花瓣形的位置变化情况就行了,方向留到最后再调整。在本例中,双色花瓣形的方向恰好正确。
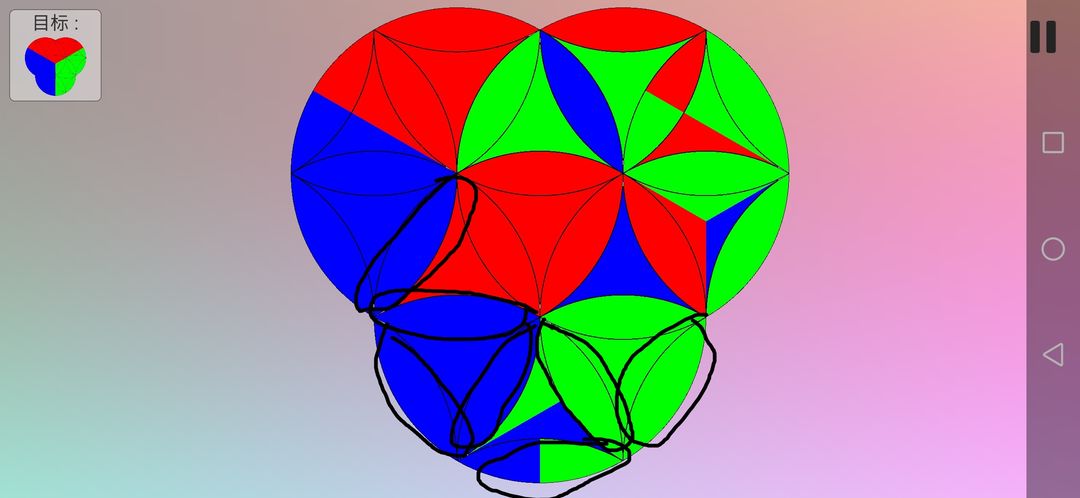
接下来复原右上角那个圆的花瓣形。这次用到7(B顺B顺A顺B逆B逆A逆),规定以下面那个圆为A旋转中心,右上角的圆为B旋转中心。7次重复才消除了不需要的花瓣形的调换,只留下两次调换,这里不用管曲三角形的变动。具体效果如下,由第一幅图到第二幅图。
我们采用第四条思路,把需要调换的色块移动到相应位置上用7(B顺B顺A顺B逆B逆A逆)进行调换。
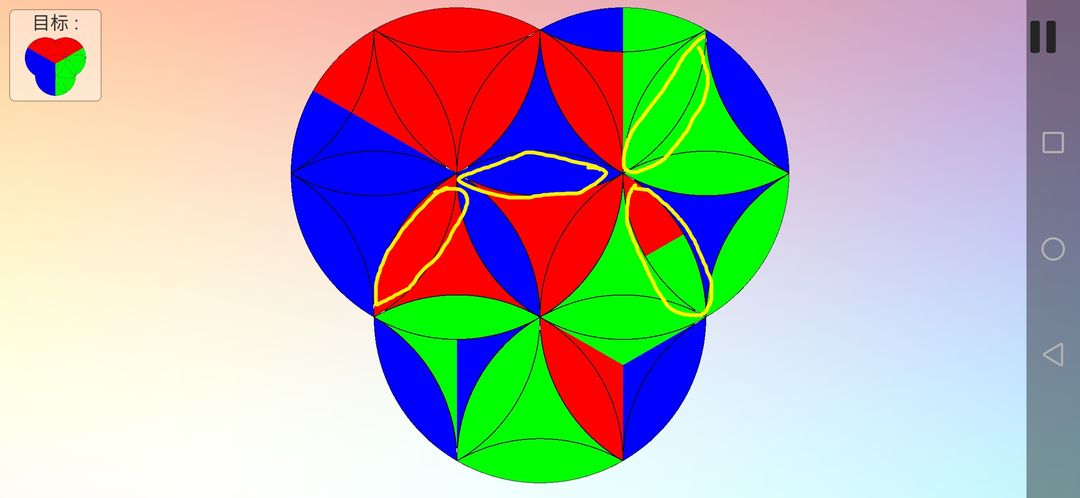
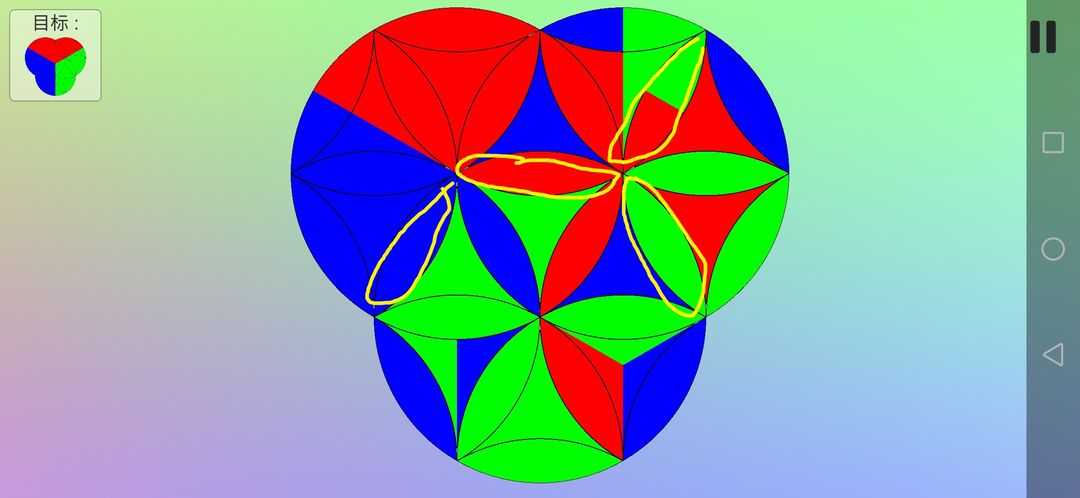
再逆着倒退回去,你看这就成功调换了2组花瓣形色块。(和第十四幅图比较)
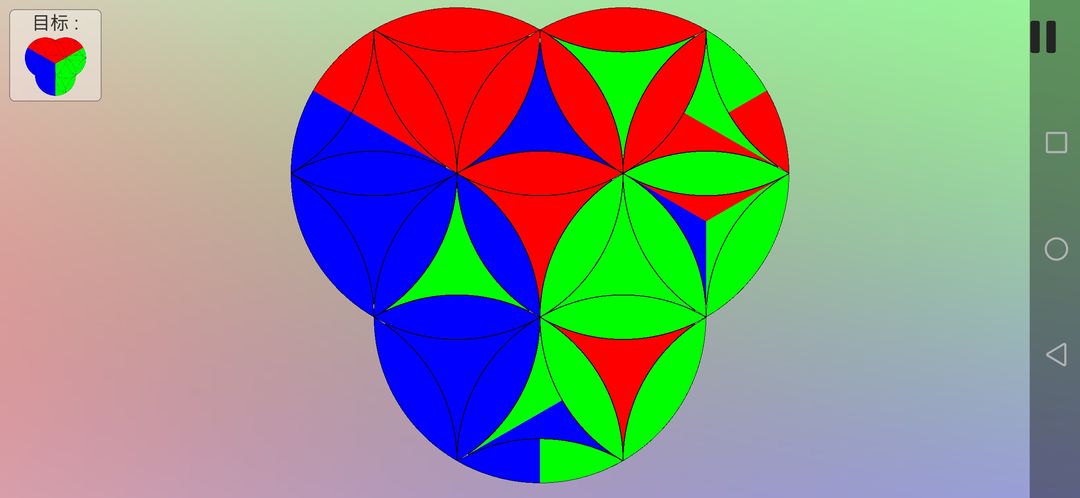
接下来一系列调换不多说了,快进到花瓣形全部复原。

我们现在开始复原曲三角形。这次用到了9(A顺B逆A逆B顺)。具体效果如下图,进行了两次调换。事实上,曲三角形可以做到只调换一次,但是那个的步数太多了,所以我抛弃了。如果你遇到只需调换一次就能把所有曲三角形的位置正确复原的情形,那么你只需要用第四条思路,把需要调换的一组色块移动到相应的调换平台上来,另一组换上颜色相同的色块就行了。
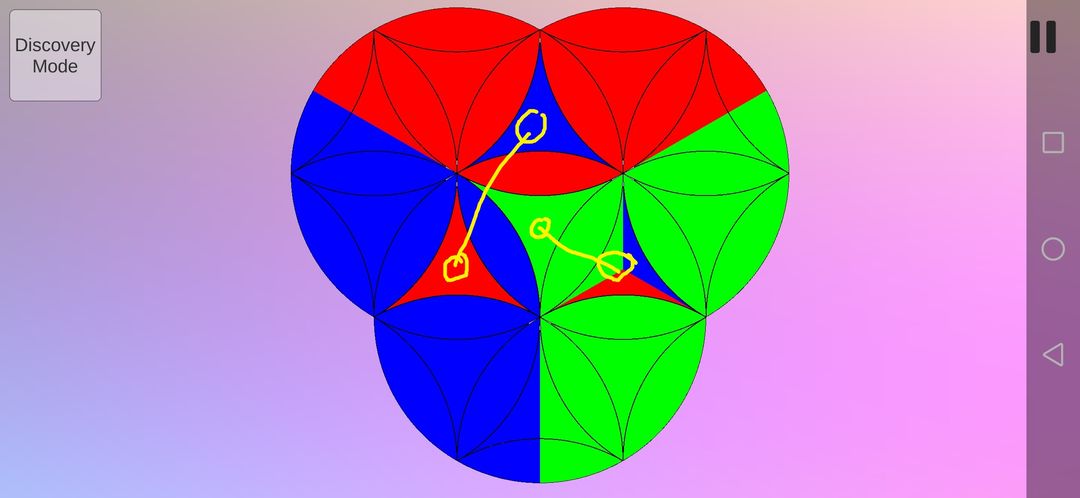
好了,不多说了,快进到所有色块的位置都还原正确。准备开始复原方向。
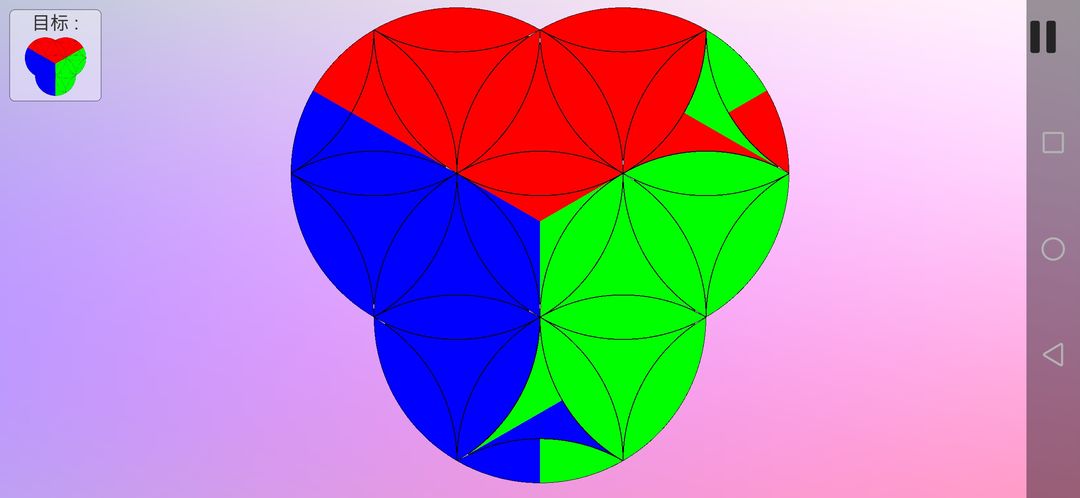
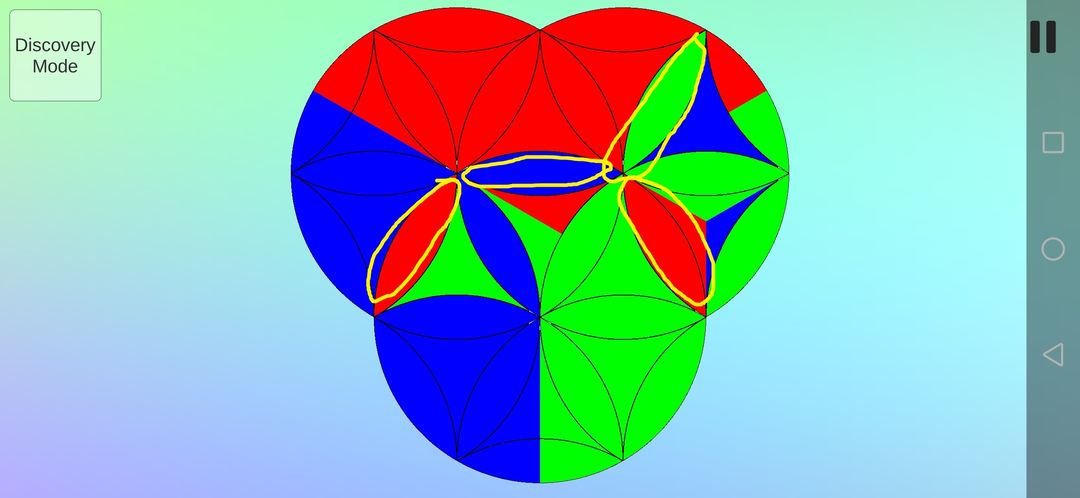
这次用到72(A逆B逆),效果如下,可看到几部分色块进行了旋转。事实上,除了黄色记号标注的的曲三角形其他都进行逆时针旋转,只不过由于同色无法区分方向。

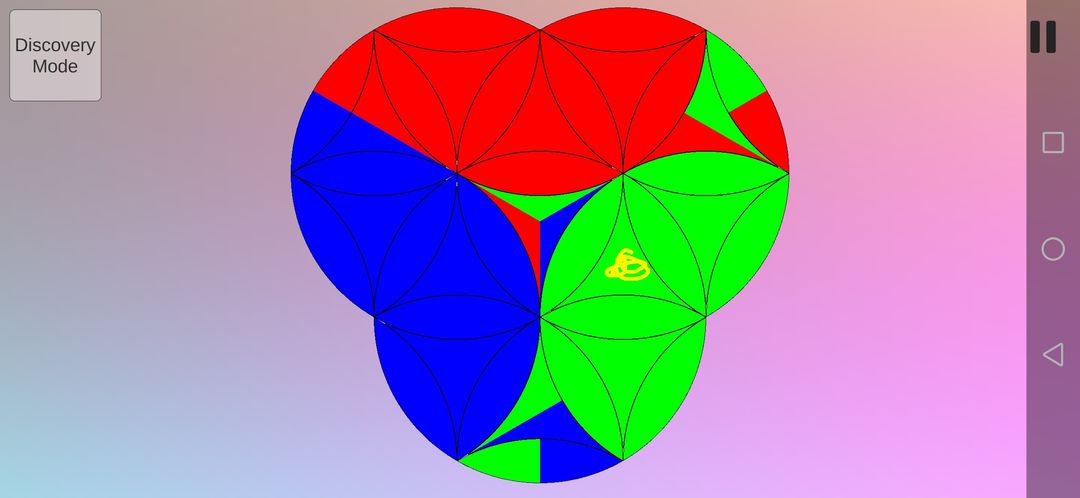
如果只需要调换花瓣形,那么用216(A逆B逆)。如果只需要调换曲三角形,那么有两种选择,第一种是把花瓣形移动到左上角的圆,避免了调换。第二种是用144(A逆B逆)。我运用了第四条思路。
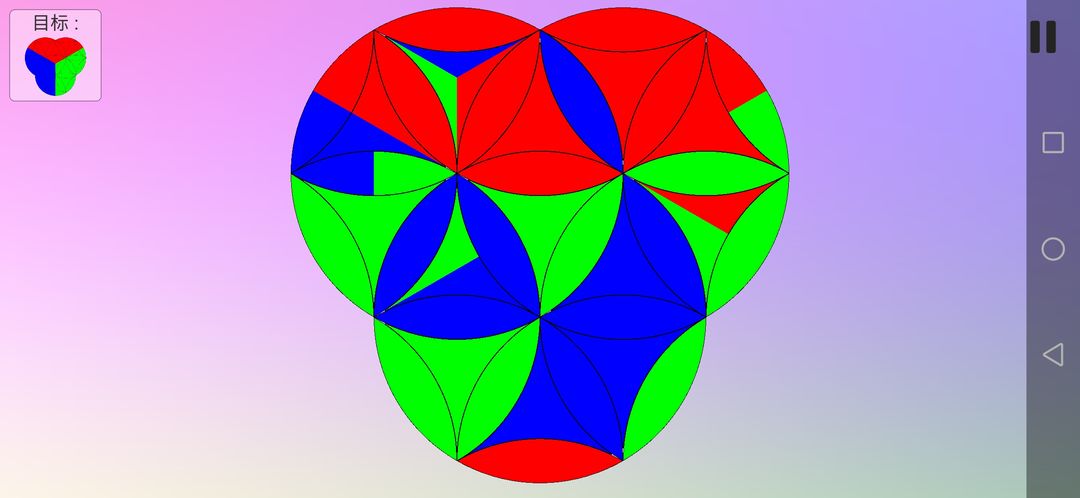
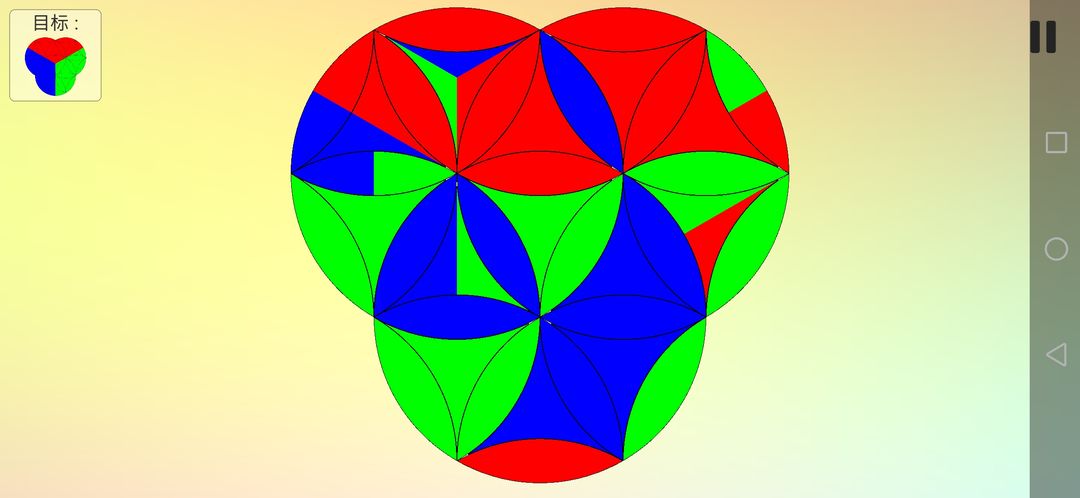
最后逆着倒退回去,完成。
总结,万变不离其宗,只要你利用好五条重要思路,解决这些谜题只是时间问题。唯一有难度的地方是要自己去确定图形中复原色块的先后顺序,这个就没什么经验可言,靠自己想。


