数据分析（九）——我们不是欧皇

再续前文，在上一篇我已经毙掉的是不是欧皇一文中，我错误地把这个抽奖求二项分布的概率，幸亏有两位评论区大佬说这并不是二项分布，而是相关事件，建议用二叉树。

通过我对前几次抽奖的总数分析，发现这竟然是一个斐波那契额数列，斐波那契额数列即是每一项等于前两项的和，如：1，1，2，3，5…

然后我继续思考为什么是斐波那契数列，然后，让我找到了规律：因为每一档抽到n个心愿的次数等于前两档抽到（n-1）个心愿的次数

当然，我还发现档数为2k的时候，抽到保底的次数为k+1，档数为2k+1的时候，抽到保底的次数固定为1.

1. 每50抽出一个仙缘，吃满保底。
2. 期间不出现任何仙缘。

接下来便是我的研究成果：

档数=抽到仙缘的个数

黑体的1，0等数字可以理解为抽到心愿的个数，

黑体下面的数字则是抽到对应个数仙缘的次数，

然后就是概率

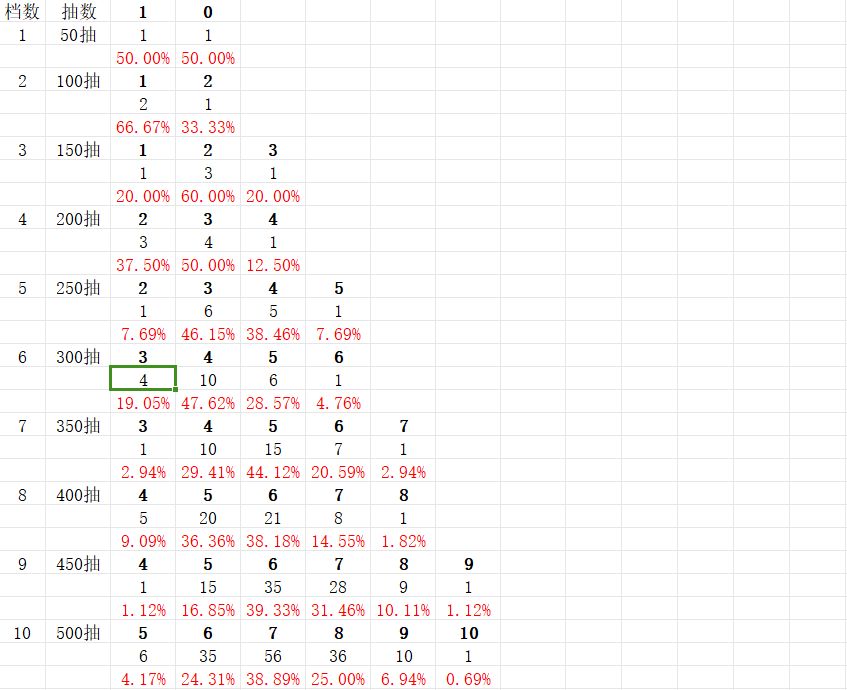
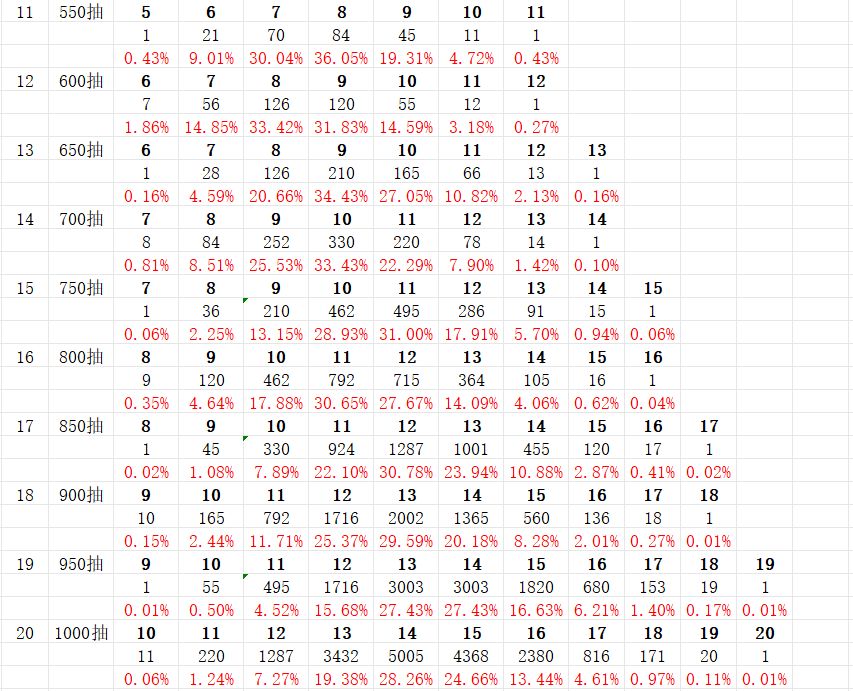
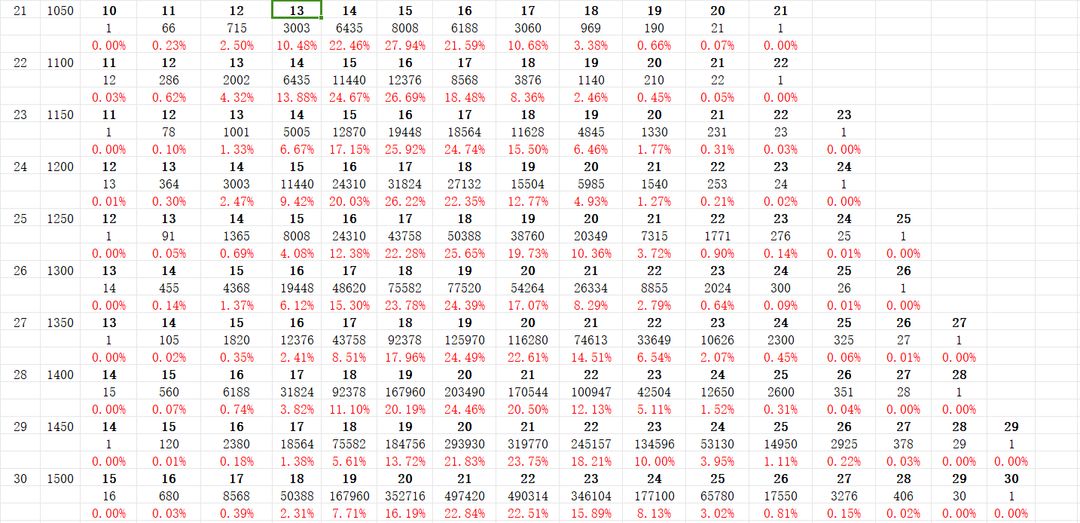
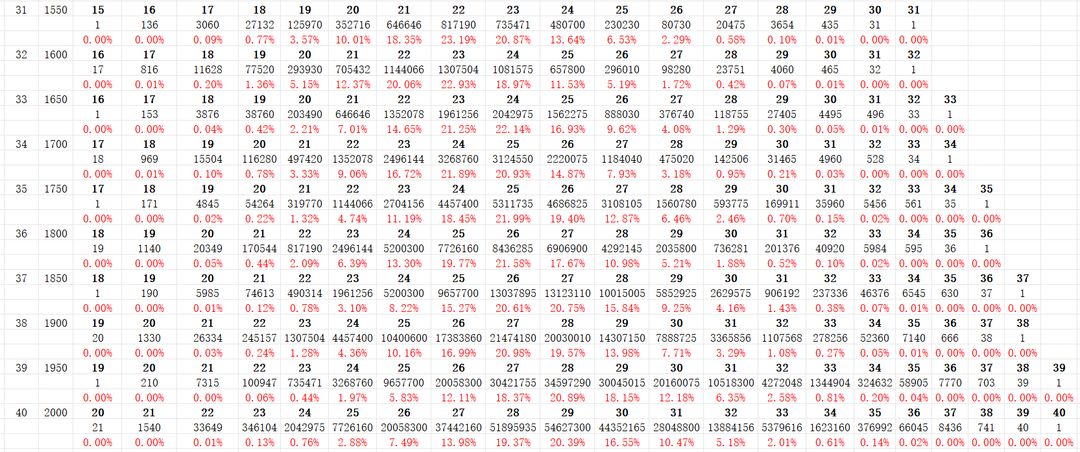
总结：

1. 不歪的概率简直难于登天，大家都会歪
2. 在抽的次数比较低的时候，全歪的概率会特别大，抽的次数多的时候，全歪的概率就没那么大了

制作不易，有什么意见尽管提