幻化成疯

逻辑岛攻略

精华修改于06/107586 浏览攻略

逻辑岛玩法为Hashi wo Kakero（日语橋をかけろ，意为建造桥梁、搭桥，简称Hashi），游戏规则为数字代表岛屿，玩家在岛屿之间搭桥，最终要符合以下要求

只能竖直或者水平方向上搭桥
桥不能相交
一对岛屿之间最多只能搭两座桥
岛屿上数字与连向该岛屿的桥数量一致
所有岛屿之间必须直接或间接相连（即从任意一个岛屿，可通过桥前往任意的另一个岛屿）

因为这些限制，可以得出不少规律（注意：目前排序仅贴主发现规律时间排序，不是实用程度排序，比如实际上岛屿群组连通分析法中部分规律比较常见且在熟悉后相对容易判断）

固定模式：观察一个岛屿，根据与该岛屿相邻（上下左右4方向）的岛屿情况，以及岛屿间最多两座桥的规律，推断桥的数量
孤岛群排除模式：观察一个岛屿，根据与该岛屿相邻（上下左右4方向）的岛屿情况，以及所有岛屿必须连通的规律，推断桥的数量
简单排除法：假设某方向没有桥，推导得出错误结果，从而断定某方向上有桥
全分支交集法：某种情况的所有可能性都推导出某一部分共同结果，则该结果为正确解
闭环分析法：根据闭环存在的规律，推导出非闭环与环外连接情况来确定桥
多解排除法：当某种情况可以推断最终结果必定会产生多解时，可以排除掉这种情况进而确定搭桥，
岛屿群连通分析法：分析岛屿群内外部接触点情况和岛屿群间外部接触点关系分析

要注意的是，当前版本（版本号1.3.4）的谜题中，绝大部分（甚至可能全部），只需要前两类规律即可解出来（不过多了解点规律对凹速度或许有用？雾）

补充（1.8.7版本）：在后续版本出现的30x30以及更大尺寸的谜题中，基本需要用到更多方法才能解

注：个人命名方法，可能听起来比较怪，问就是想不到好名字

一、固定模式

说明：使用如41**格式来表示，第一个数字表示要观察的岛屿的数字，后面数字或*代表相邻岛屿可搭桥数量（数字-已搭桥数量），*代表可搭桥数量≥2，这些固定模式不建议硬背，理解中记忆，列出来是为了防遗漏，实际上因为要减去桥的数量、距离可能很远、附近岛屿较多等原因，就算是简单的模式，也可能很难发现

规律（可忽略）：记岛屿数字 n，四向岛屿中可向中心岛屿搭 1 座桥的岛屿数量为 n1，可搭 2 座桥的岛屿数量为 n2

当 n1+2*n2-n=0 时，所有方向可搭桥数量与中心岛屿数字相等，即全连接刚好连满

当 n1+2*n2-n=1 时，全连满状态下去掉一座桥，显然 n2 的岛屿至少会剩一座桥，即向 * 各搭一座桥

只有一个方向可搭桥情况，直接搭桥(1=1+2*0/1=0+2*1-1)

同上(2=0+2*1)

最多向1搭1座桥，所以至少向*搭1座桥(2=1+2*1-1)

不可能向一个方向搭3座桥，所以两个方向都必须有一座桥(3=0+2*2-1)

直接搭满了(3=1+2*1)

311*

*以外最多搭2座桥，所以*至少搭一座桥(3=2+2*1-1)

搭满了(4=0+2*2)

41**

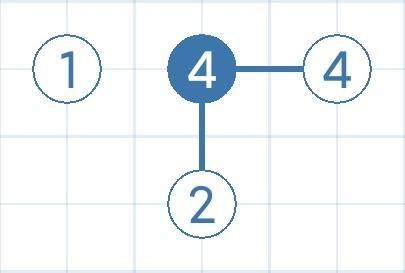
两个*至少搭3座桥，类似3**(4=1+2*2-1)

411*

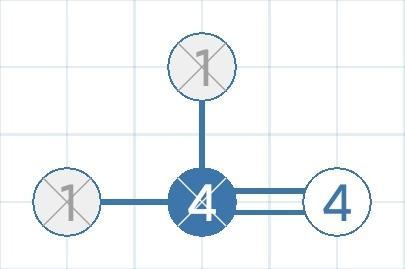
搭满了(4=2+2*1)

4111*

3个1最多搭3座桥，所以*至少搭1座桥(4=3+2*1-1)

5***

任意方向不搭桥都不可能满，所以三个方向都有桥(5=0+2*3-1)

51**

搭满了(5=1+2*2)

511**

两个1最多搭2座桥，所以两个*至少搭3座桥，类似3**(5=2+2*2-1)

5111*

搭满了(5=3+2*1)

6***

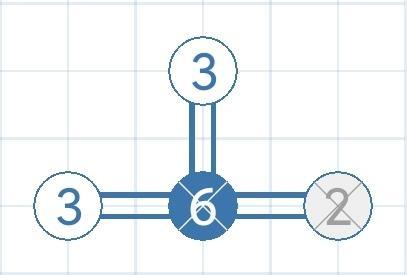
搭满了(6=0+2*3)

61***

1最多搭1座桥，所以3个*至少搭5座桥，同5***(6=1+2*3-1)

611**

搭满了(6=2+2*2)

7***

类似5***(7=0+2*4-1)

71**

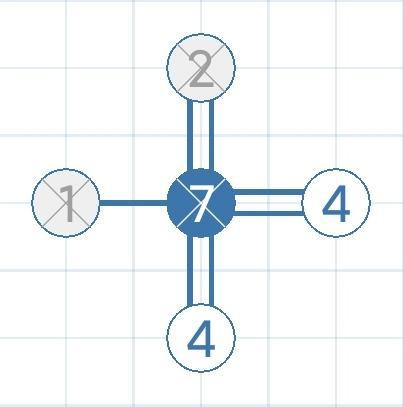
搭满了(7=1+2*3)

8***

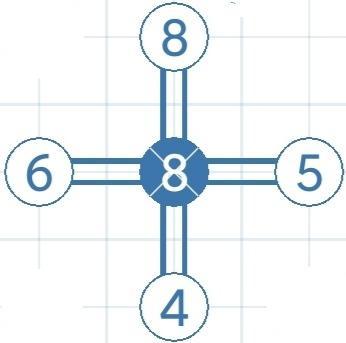
搭满了(8=0+2*4)

二、孤岛群排除模式

因为规则中有要全连通的要求，所以可以通过排除孤岛群来确定连线，与上面固定模式不同，这里数字不能简单用原数字-已连桥数量，还需要满足与除了*以外方向为不可再向外连接的孤岛状态。规律为除了某个方向外其他岛屿数字可搭桥数量加起来等于岛屿数字，理解中记忆

规律（可忽略）：定义自由岛屿为中心岛屿与之连接后在该区域无法确定是否会产生孤岛情况的岛屿，有以下两种情况

1. 岛屿可搭桥数量大于中心岛屿可搭桥数量

2. 与其他岛屿相连，且相连的岛屿中至少存在一个岛屿处于未连接满状态

记中心岛屿数字为 n，相邻岛屿中自由岛屿数量为 nx ，其他岛屿中，可搭桥数量为 1 的岛屿数量为 n1，可搭桥数量为2的岛屿数量为 n2 （当 n=1时，n2 设为 0 ）

一、当 nx>1 时：连接方式无法确定

二、当 nx=1 时：

当 n2=0 或 n1+2*n2-n=0 时，除自由岛屿外，任意连接均会产生孤岛，因此可确定中心岛屿至少向自由岛屿搭一座桥，否则无法确定

三、当 nx=0 时：（由于不可连满，可推导出必定有 n<n1+2*n2）

当 n2=1时：必须向 n2 搭一座桥（不能多也不能少，此时可能进而判断 n2 的搭桥情况），然后继续下面判断

当 n1+2*n2-n=1 时：有第一类规律可知至少向 n2 各搭一座桥；此时相当于全连满时去掉一座桥的情况，去掉的桥不可能是 n1 ，因此 n1 必须各搭一座桥。结论为向所有方向各搭一座桥

当 n1+2*n2-n=2 时：即全连满情况去掉两座桥，此时不可能让某个n2的岛屿桥全部去掉，因此向所有 n2 方向各搭一座桥

11*、111*、1111*

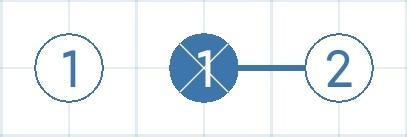
nx=1且n2=0

nx=1且n1+2*n2-n=0

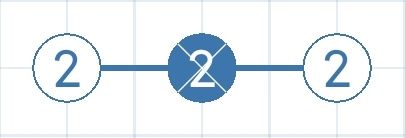
可看成两次22*模式(nx=0且n1+2*n2-n=2)

221 、2211、22111(nx=0且n2=1)
211*、2111*

nx=1且n2=0

321*

nx=1且n1+2*n2-n=0

3221

可看做两个321*模式(nx=0且n1+2*n2-n=2)

3211

只有一个2、(nx=0且n2=1且n1+2*n2-n=1)

32111 (nx=0且n2=1)
3111*

nx=1且n2=0且n1+2*n2-n=0

422*

nx=1且n1+2*n2-n=0

4221 (nx=0且n1+2*n2-n=1)
4222

可看做3个422*模式(nx=0且n1+2*n2-n=2))

5221*

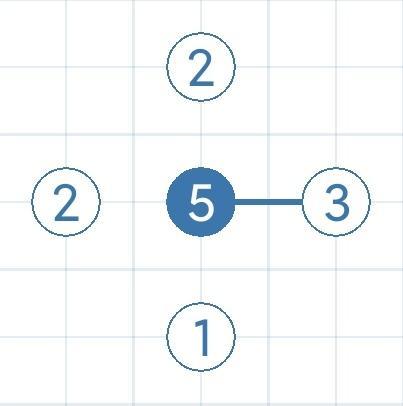
nx=1且n1+2*n2-n=0

52211

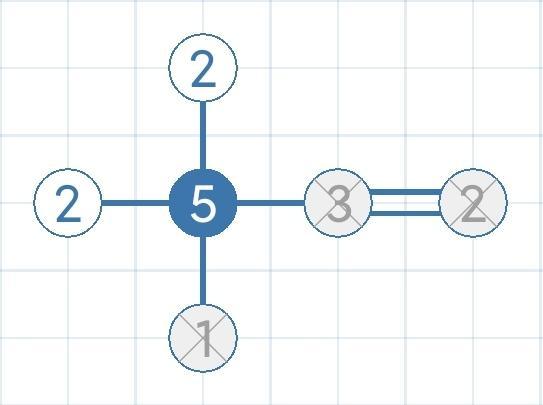
不向任意1搭桥情况都是孤岛+511**固定模式(nx=0且n1+2*n2-n=1)

此处3向外连接的的所有岛屿（岛屿2）均处于连满状态，所以可等效成3-2=1

52221

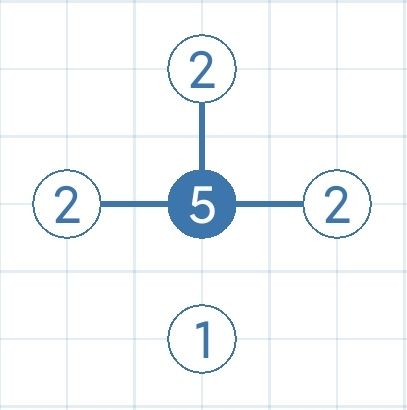
3次5221*模式(nx=0且n1+2*n2-n=2)

6222*

nx=1且n1+2*n2-n=0

62221 (nx=0且n1+2*n2-n=1)
62222

nx=0且n1+2*n2-n=2

三、简单排除法

通过假设某情况，根据该情况推导产生错误结果时，可以排除掉这种情况，此时有可能可以得出某些必定存在的桥，下面只是举例一些简单的情况，复杂情况可能需要自己分析，a向b表示可能存在a个可搭桥方向的数字b岛屿3。此处*可能为数字1

规律（可忽略）：主要情况有两种

1. 某方向可搭桥数量 -1 后进行基础模式判断，如果判断有结果，用这个结果来解题，如果解题时发现错误，则原方向（数量-1的方向）再搭一座桥

2. 某已搭桥数量为0搭桥方向，将该方向可搭桥数量设为0，进行孤岛排除模式判断，如果判断有结果，用这个结果来解题，如果解题时发现错误，则原方向（数量设为0的方向）至少搭一座桥

2向1（1**）

数字1的岛屿必定往其中一个方向搭桥，记两个方向分别为 a b，假设a方向有桥，发现错误，则b方向搭1座桥，其他方向同理，假如都未出现错误，则不确定

2向2（2**）

数字2的岛屿必至少往其中一个方向搭桥，记两个方向分别为 a b，假设a方向有桥，发现错误，则b方向搭2座桥，其他方向同理，假如都未出现错误，则不确定

3向3（3***）

数字3的岛屿至少往2个方向搭桥，记三个方向分别为a b c，假设a b方向有桥，推导出错误结果，那么c方向至少有1座桥，其他方向同理

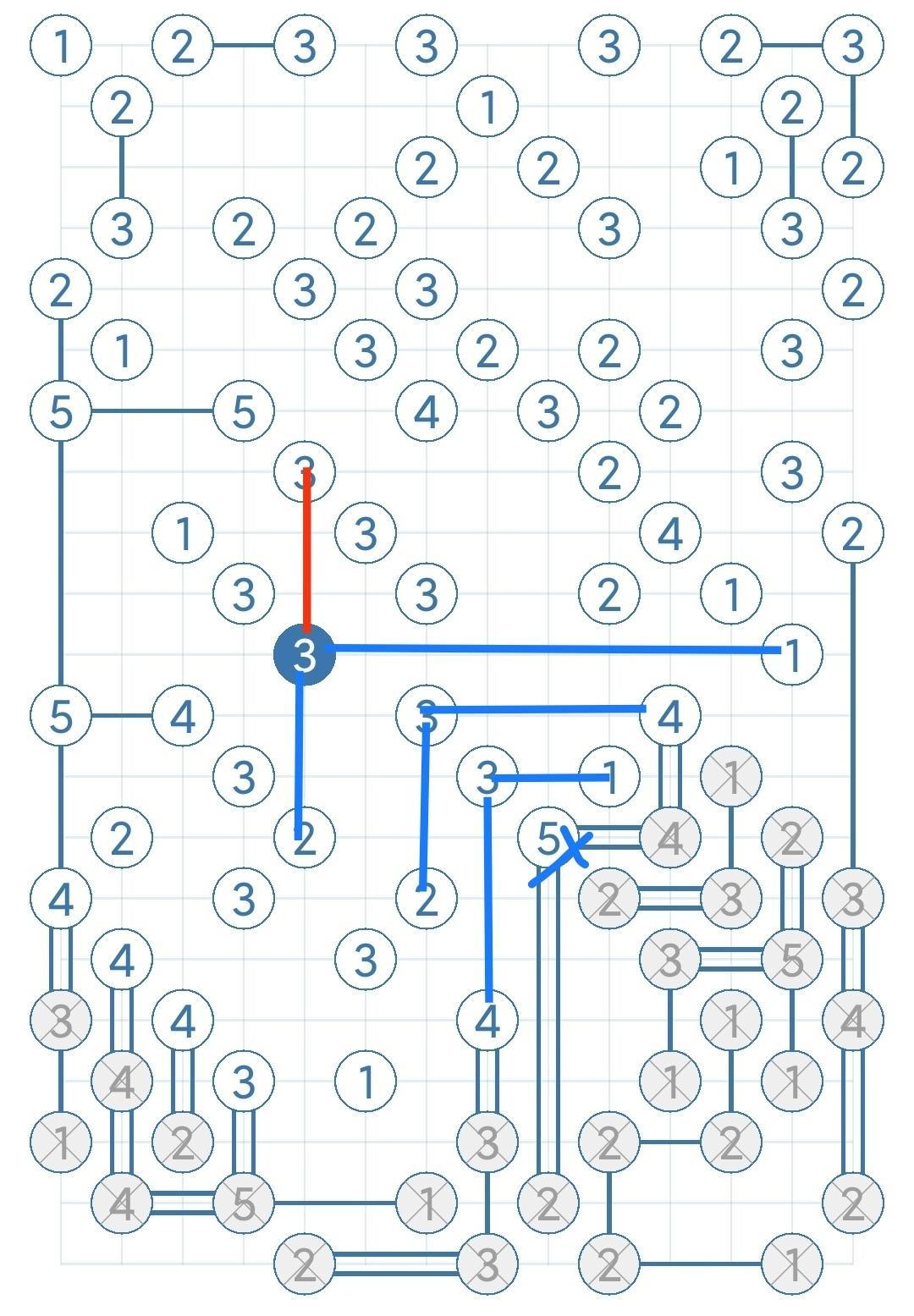
蓝色为假设推导方向，红色为推导结果

3向4（4***）

数字4的岛屿至少往2个方向搭桥，记三个方向分别为a b c，假设a b方向有桥，推导出错误结果，那么c方向必有有2座桥，其他方向同理

4向5（5****）

数字5的岛屿至少往3个方向搭桥，记四个方向分别为a b c d，假设某a b 方向有桥，推导出错误结果，那么c d方向分别至少有一座桥，其他方向同理

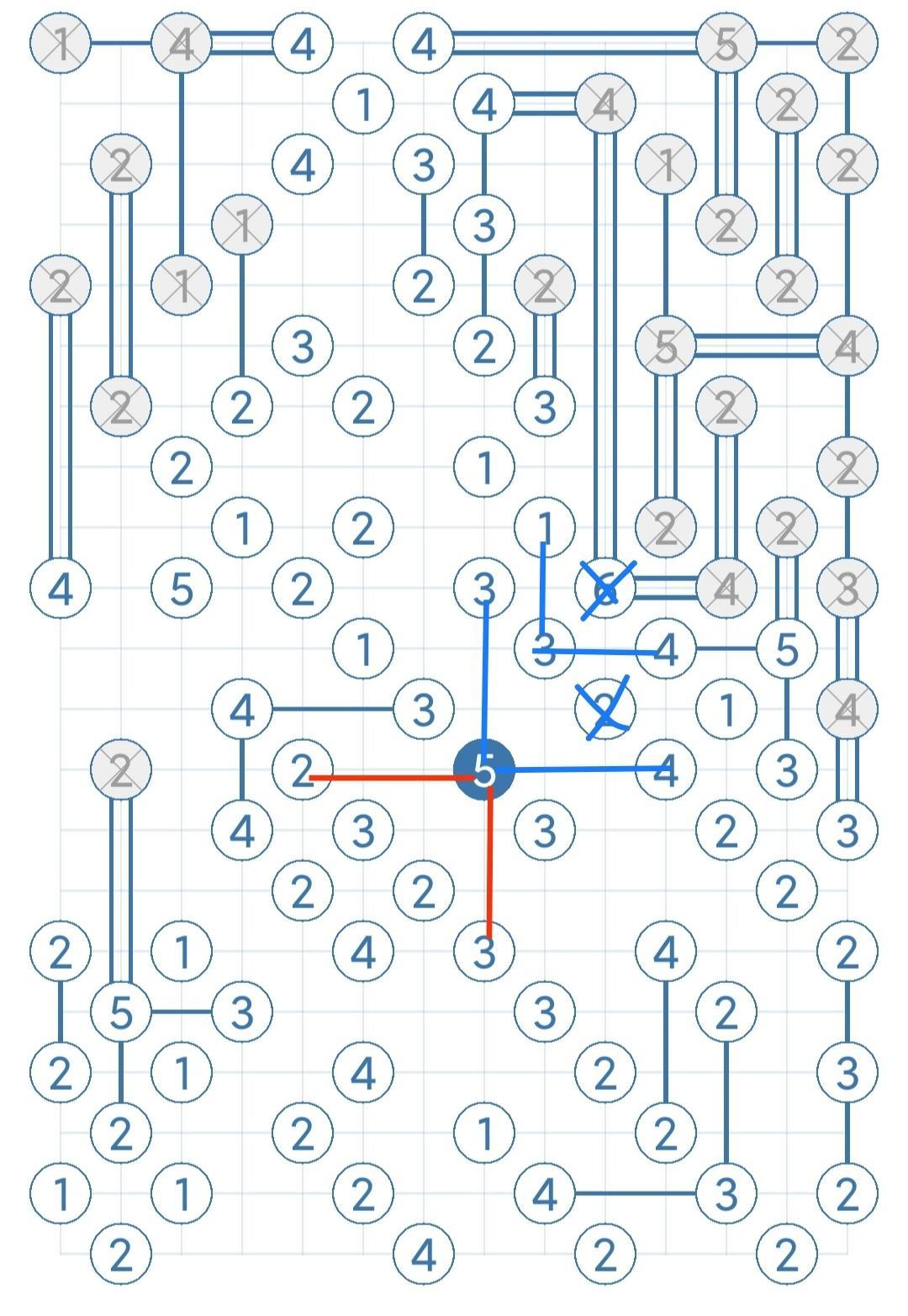
4向6（6****）

数字6的岛屿至少往3个方向搭桥，记四个方向分别为a b c d，假设某a b 方向有桥，推导出错误结果，那么c d方向分别必定搭2座桥，其他方向同理

等效情况

例如41***，除了数字1的方向外三个方向至少搭3座桥，因此至少往两个方向搭桥，与3**情况一样

注意：此图为初版未保证连通和唯一解时的非标准Hashi谜题的图，因此结果会出现多解或孤岛为正常现象

四、全分支交集

假如某处有3种可能情况，且为所有可能性（并集为全集），这3种情况得出的推导结果有交集，则此交集为正确解

旧版本图注意事项同上

数字为4的岛屿可与三个方向连线，上下方向上至少一个方向有桥，因此有三种可能，向上有桥，向下有桥，或者都有桥，图上蓝色和绿色分别代表两种可能，上下都有桥的情况与蓝色类似，就不画了，可以看出共同结果为红线的两个3相连因此红线为正确解

五、闭环分析法

将一系列岛屿连成一个环，如果该环上岛屿均不能再继续往环外搭桥，则称该环为闭环，闭环与环上桥的会有一定规律，通过这些规律可以进行推导

闭环上每座桥会为环内两个岛屿数字分别+1，因此闭环内岛屿数字总和减去向环外搭桥数量结果一定为偶数

假如闭环上除了相邻岛屿以外的岛屿均无法连接，且环内岛屿数量为偶数，将相邻岛屿分开，相间岛屿组成组一起，分成两组，因为环上的桥必定是两组岛屿之间进行的连接，所以两组岛屿数字总和（减去与环外搭桥数量）相等。特殊的，假如环内不同组的岛屿之间存在其他连接，不破坏桥必定是两组岛屿之间进行连接的规律，因此此规律仍然适用

根据上面规律，假如一个环，与环外存在较少连接点时，可能可以推导出该连接点的搭桥情况，如下图

旧版本图注意事项同上

红色圈起来的环（左上开始顺时针4342，减去往外搭桥数量为3342）），按相间岛屿分成两组，左上4和右下4一组，左下2和右上3一组，环上存在两个外部连接点为左上和右下，都在第一组，根据第一组数字总和（减去向外搭桥数量）为7，第二组数字总和为5，可知第一组必定向外搭2座桥，再根据左上和右下分别可最多可向外搭1座桥，因此左上和右下分别向外搭1座桥。顺便一说，将数字减去环内已搭桥数量（2121）结果也是一样的

另外要注意的是，环内部可能存在岛屿，只要不能与环上岛屿搭桥就不影响，有时候可用于进行分析的环可能并不好找