下载 App
EH的数独杂谈#10 超实用技巧整理
修改于2023/09/191.1 万浏览攻略
--------目录--------
一、最基本的技巧
1. 摒除与唯余
2. 数组
3. 区块
二、致命与致死结构类技巧
1. 唯一矩形（UR）
2. 全双值格致死（BUG）
三、各种Wing
1. X-Wing（二链列）
2. XY-Wing（双分支匹配）
3. XYZ-Wing（三分支匹配）
4. W-Wing
四、链的常用构型
1. 双强链
2. 远程数对
--------------------
在综合篇中，笔者将为大家展开新的视角，通过对构造、毛刺、秩理论等思想方法的讲解，帮助大家更灵活地运用现有的技巧解决高难度的数独题目。
作为综合篇的第一章，有必要先将常用的技巧进行总结，以免后续内容给读者造成理解上的困难。
一、最基本的技巧
1. 摒除与唯余
摒除与唯余这两种方法，只要各位接触过数独并了解它的规则，不学也是学了。
摒除分为两大类：宫摒除和行列摒除。
宫摒除实例见图10-1-1。根据数独规则，数字3在第5宫里只有一种填法。
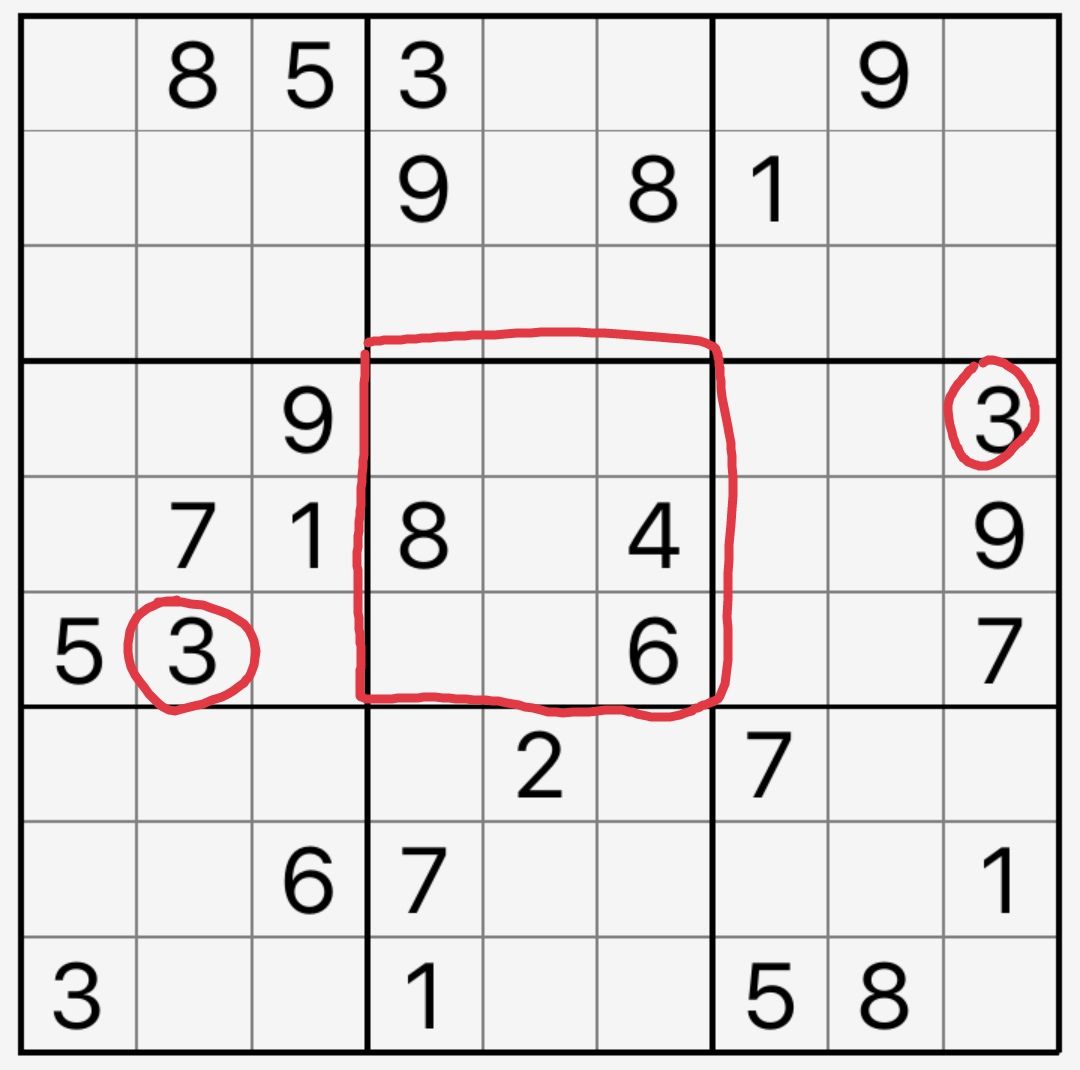
图10-1-1 宫摒除
行/列摒除实例见图10-1-2。在第4列上，数字7的填法只有一种。
虽然宫摒除和行列摒除都是基于数字的位置进行填数操作，但宫摒除观察起来更方便。
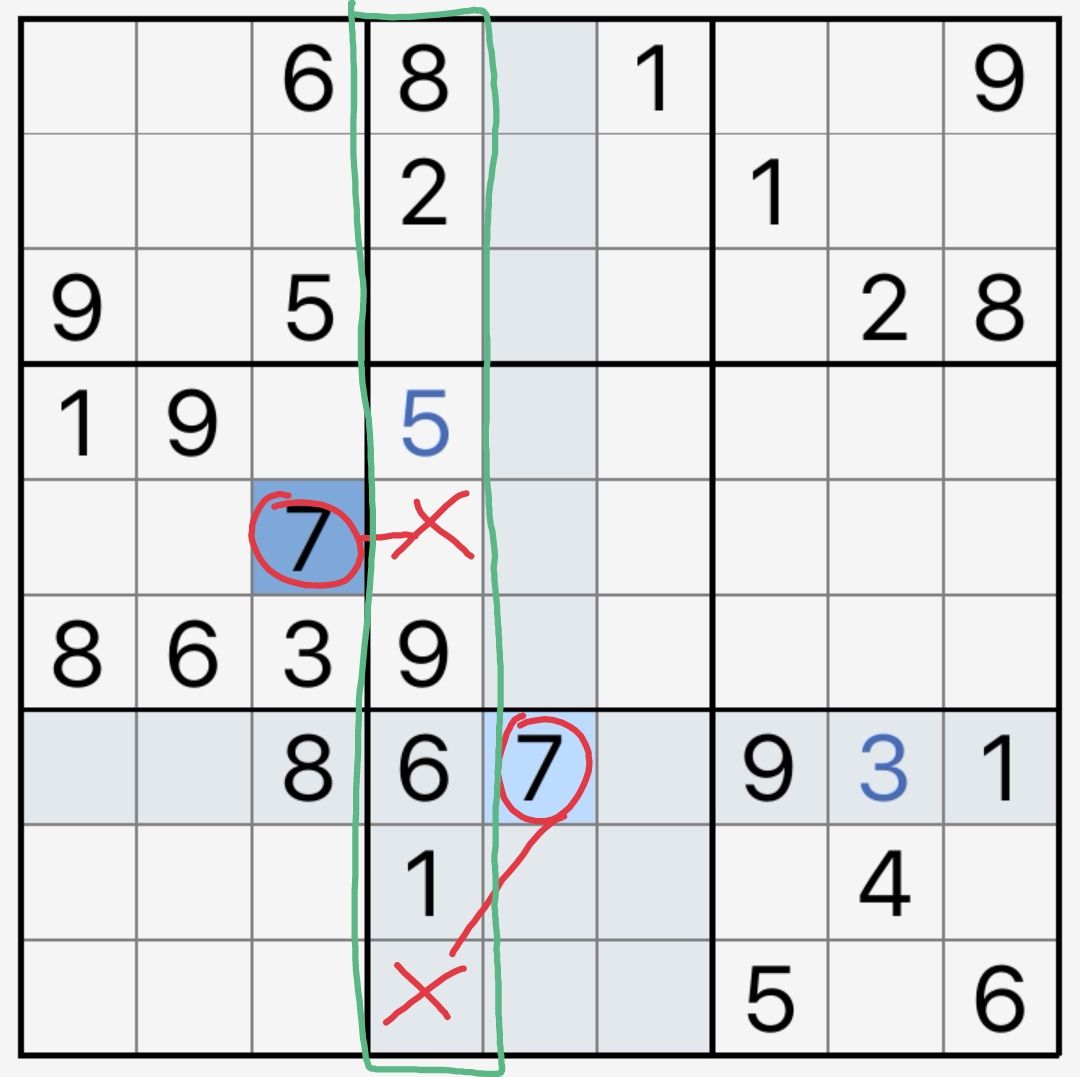
10-1-2 列摒除
相对于摒除“用同一种数字解题”的思想，唯余则是使用“一个单元格”，观察其能看到的数字从而得解。
别看我说得这么绕，其实唯余最简单的形式你总能见到，比如图10-1-3的第一行：
10-1-3 Full House
这种一行/列/宫里只有一种数字未填的情况，就算是唯余最简单的形式了，有时被称作“满汉全席”（Full House）。
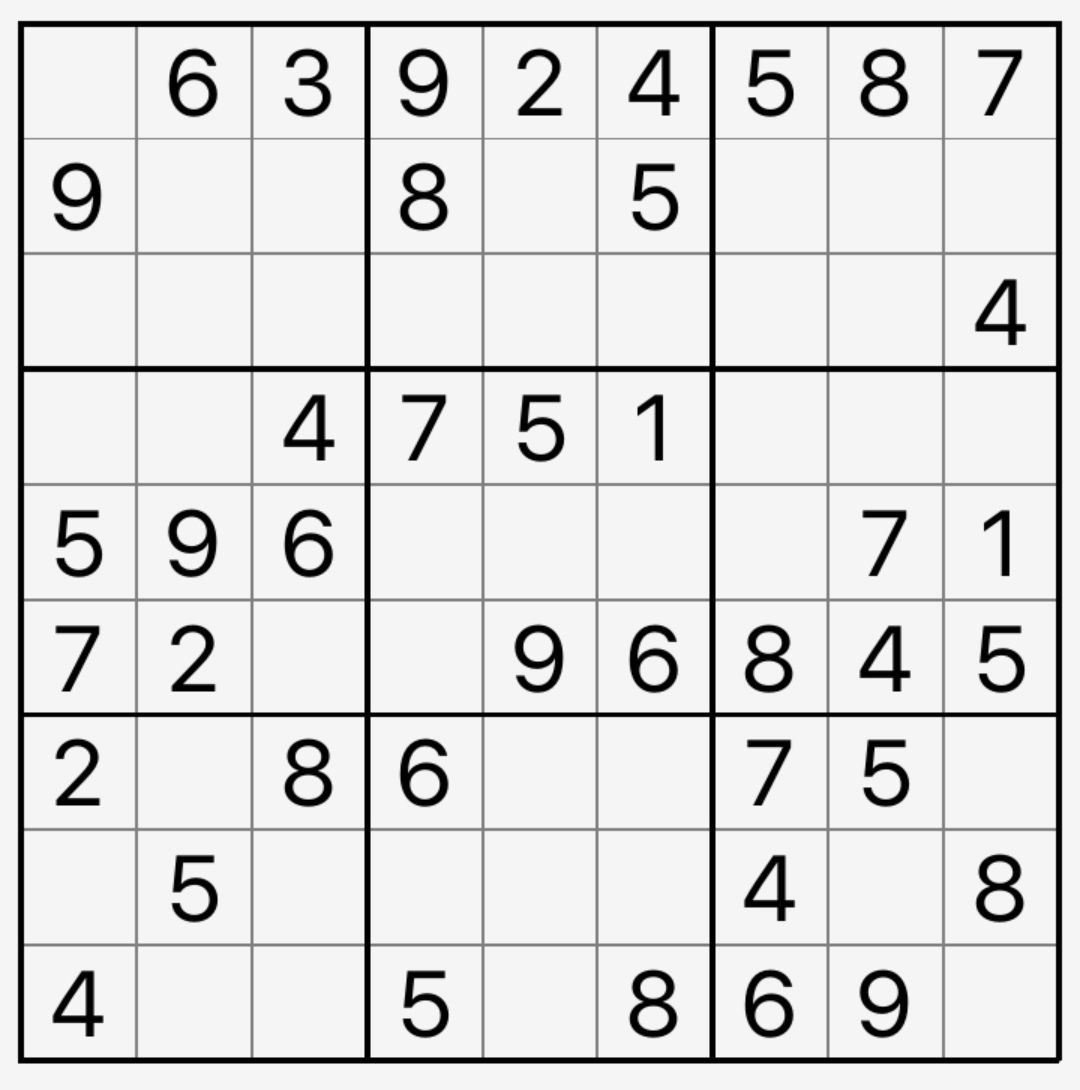
当然唯余的一般形式见10-1-4，提示数遍及行、列、宫。试着理解一下高亮的蓝色单元格应该填多少吧！
10-1-4 唯余的一般形式
2. 数组
数组描述了一种“n个数字填入同一行/列/宫的n个单元格”的情形，虽然不能直接确定具体的填数方式，但对外仍然有排除的功能。
数组也分两种：显性数组和隐性数组。
显性数组的实例如图10-1-5所示。注意到r5c12（绿色框部分）必然一个填4，另一个填5。现在考察蓝色格，其所在的列还有347三种数字未填入。这个蓝色格能被左边的给定数7和45数组看到，所以不能是4和7，必须填3。
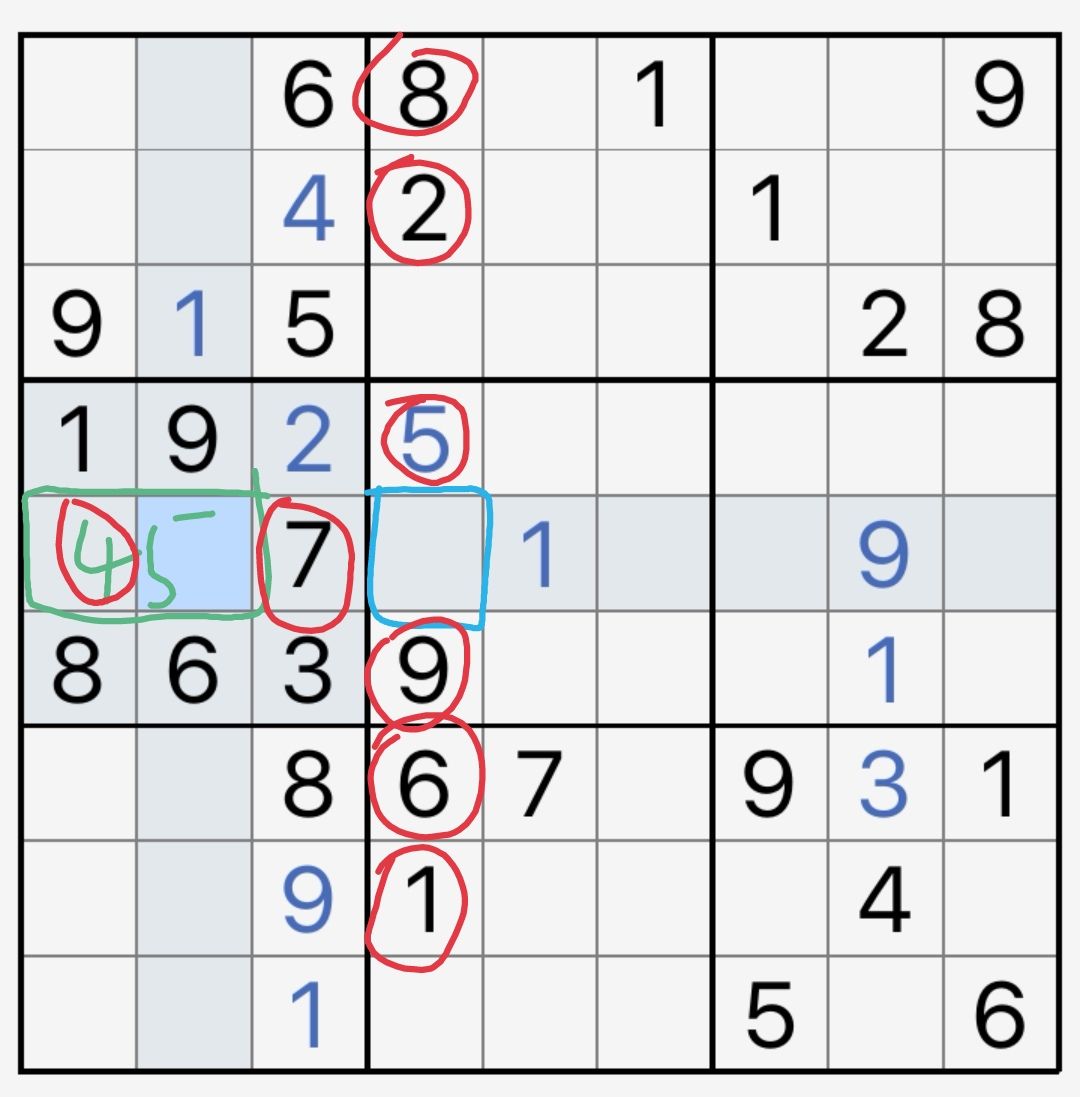
图10-1-5 显性数组
隐性数组的实例如图10-1-6所示。2宫还有256789六种数字未填。由于橙色格子的作用，2宫里的紫色格子都不能填568三种数字的任何一种。也就是说，568三种数字在2宫被“挤进了”红框的三格内。所以红框三格只能填568，进而紫色格子只能填279。此后，根据第三行的给定数79，唯余得到r3c4=2；根据第6列的给定数8，摒除得到r3c5=8。
细心的朋友们会发现，r3c4=2其实只需要一步唯余就能得到，r3c5=8也只需要一步摒除就能得到。但笔者是想借助这个例子说明显性数组与隐性数组的不同之处：前者利用明确的数组进行对外排除，后者则是通过分析区域内多种数字的占位进行对内分组。
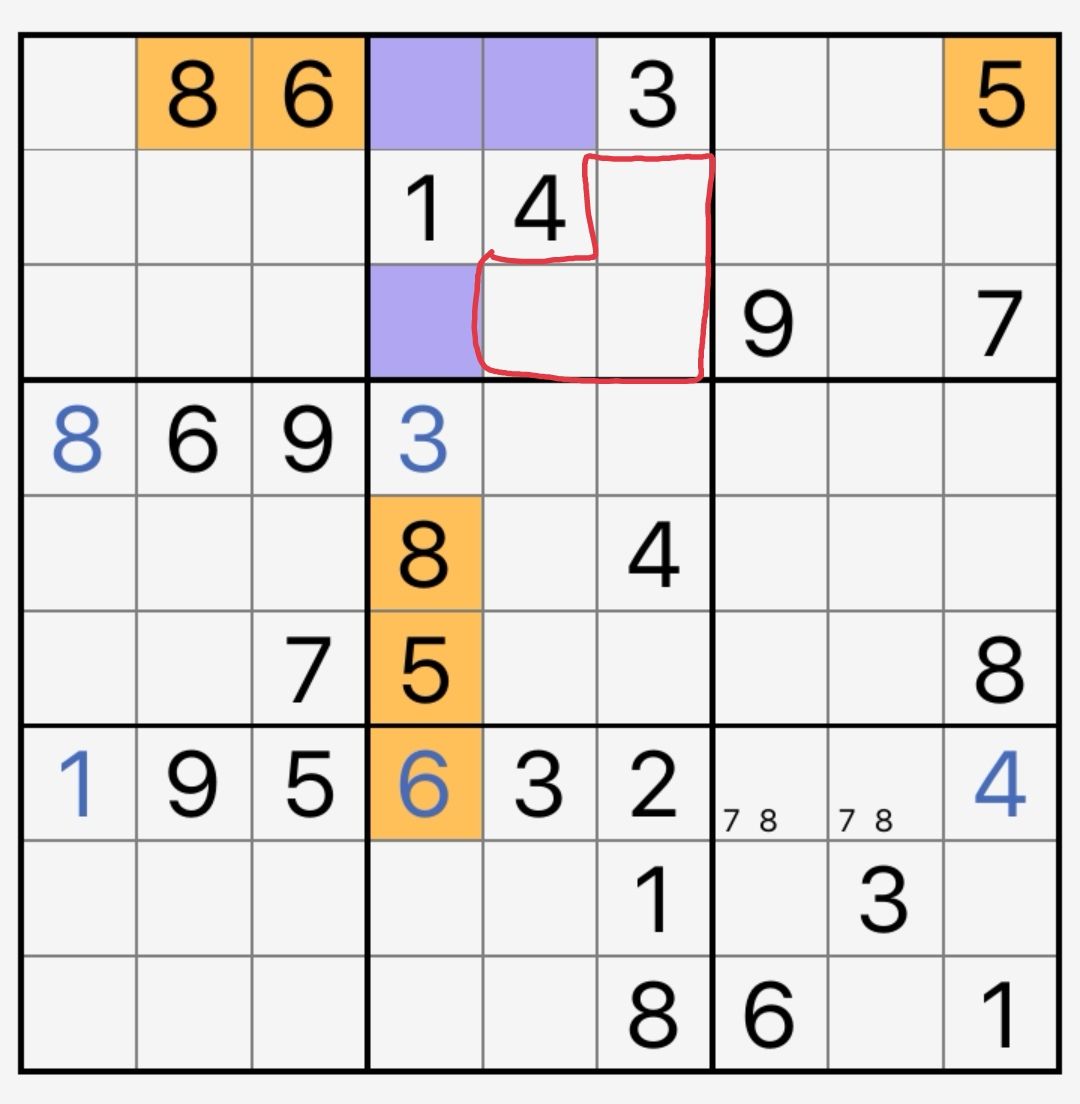
图10-1-6 隐性数组
3. 区块
如果说数组是通过多种数字占位来排除，那么区块则是用一种数字占位来排除。
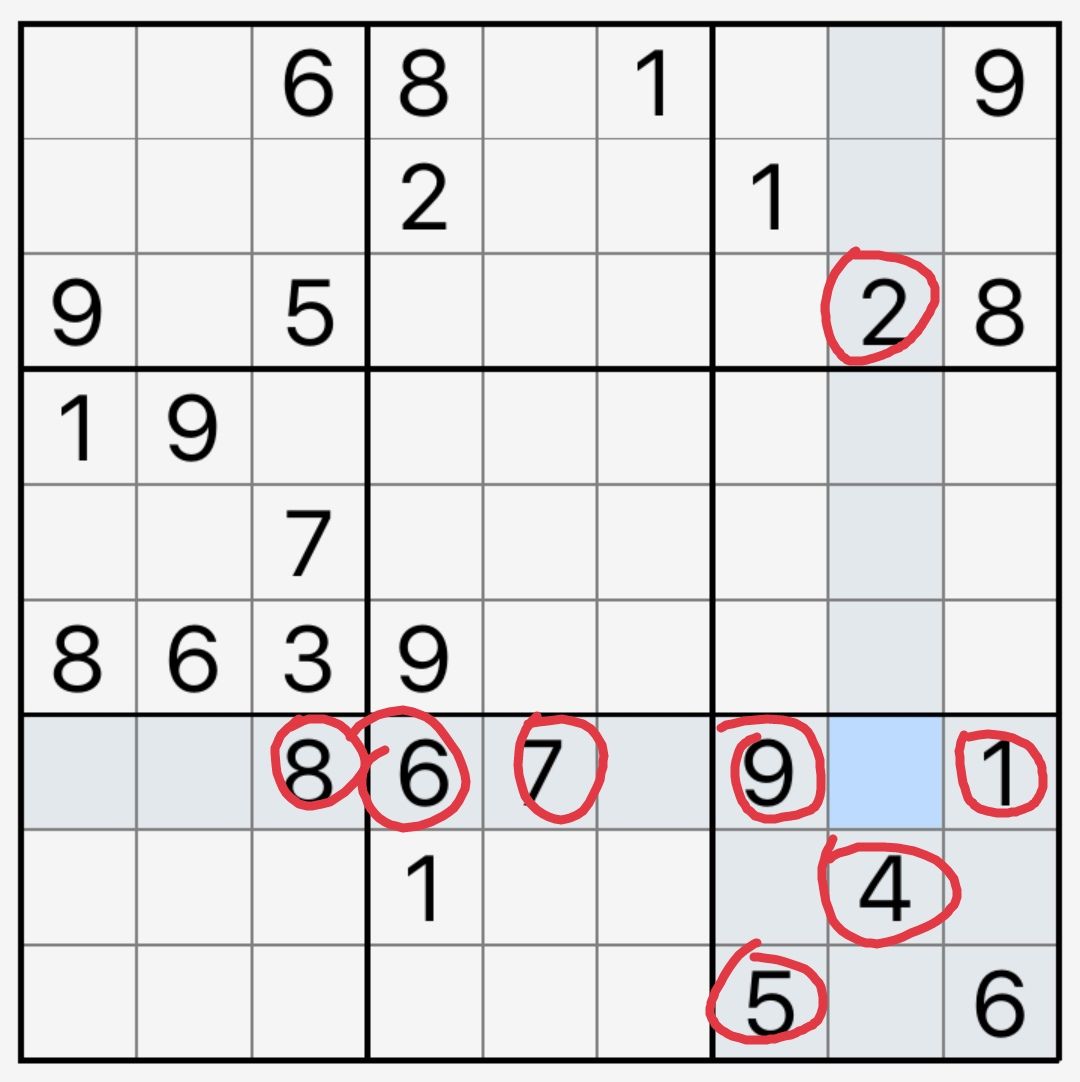
例如图10-1-7，我们分析4列里填入数字5的情况，会发现r39c4两格可以直接被5看到，不能填5。同时，1宫5向下也能对4宫作摒除，导致4宫的5只能填入r5c12两格内，因其位于同一行，而构成一个有效的区块。这样，r5c4也不能填5，从而r4c4=5。
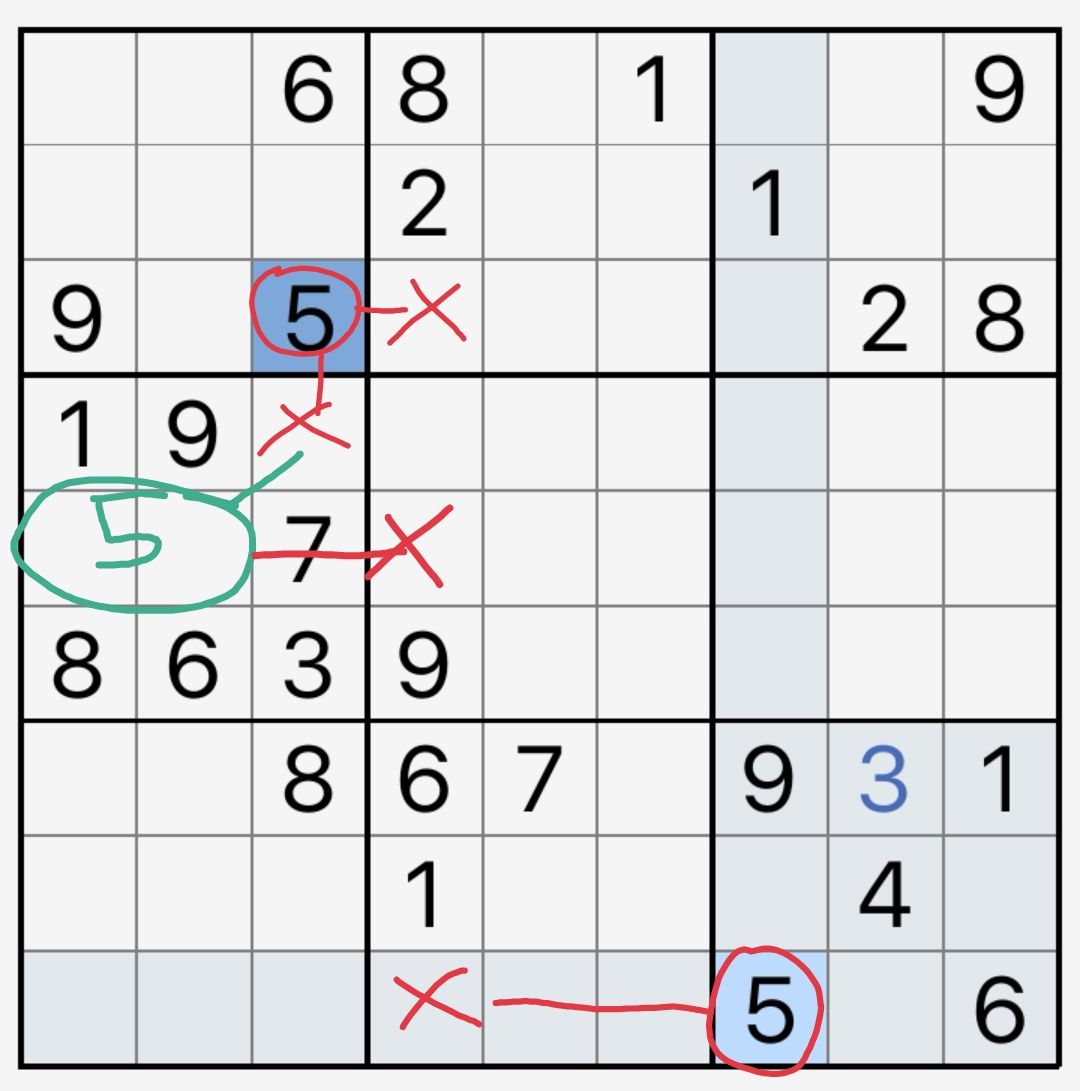
图10-1-7 区块
像数组一样，区块里的数字也暂时不知道要填在哪儿，但无论如何都可以对外排除一些填数情况，甚至直接得到填数。
这四种基本技巧构成了数独的最基础方法。它们虽然思路各异，各有特点，却又蕴含着内在的联系，需要大量的练习方能发掘。
二、致命与致死结构类技巧
请再次注意：致命与致死结构类技巧都必须建立在“数独有且仅有唯一解”的基础上。
1. 唯一矩形（UR）
唯一矩形是最简单、最好观察的一类的致命结构。正因为其形式太过简单，在原则上只需要用到数组/区块的题目里，你依然可以巧用UR来逃课！
关于UR的知识点，本人在下面的链接里进行过整理。没有阅读过的小伙伴建议仔细阅读；对于已经掌握的小伙伴，为了避免实践中出错，请再次复习UR成立的条件，尤其是第二条：
（1）必须是涉及4个单元格内的两种候选数，这4格必须构成矩形。
（2）这4格只能分属两个宫内。
2. 全双值格致死（BUG）
致死结构其实是致命结构的延展。在致命结构的篇章，我们说到“局部多解，就等同于全盘无解”。特别地，当这个局部恰好就等同于全盘的时候，就无所谓“局部多解”，只剩下“全盘无解”，也就是致死。
为了讲清楚“致死”的逻辑，请看图10-2-1：
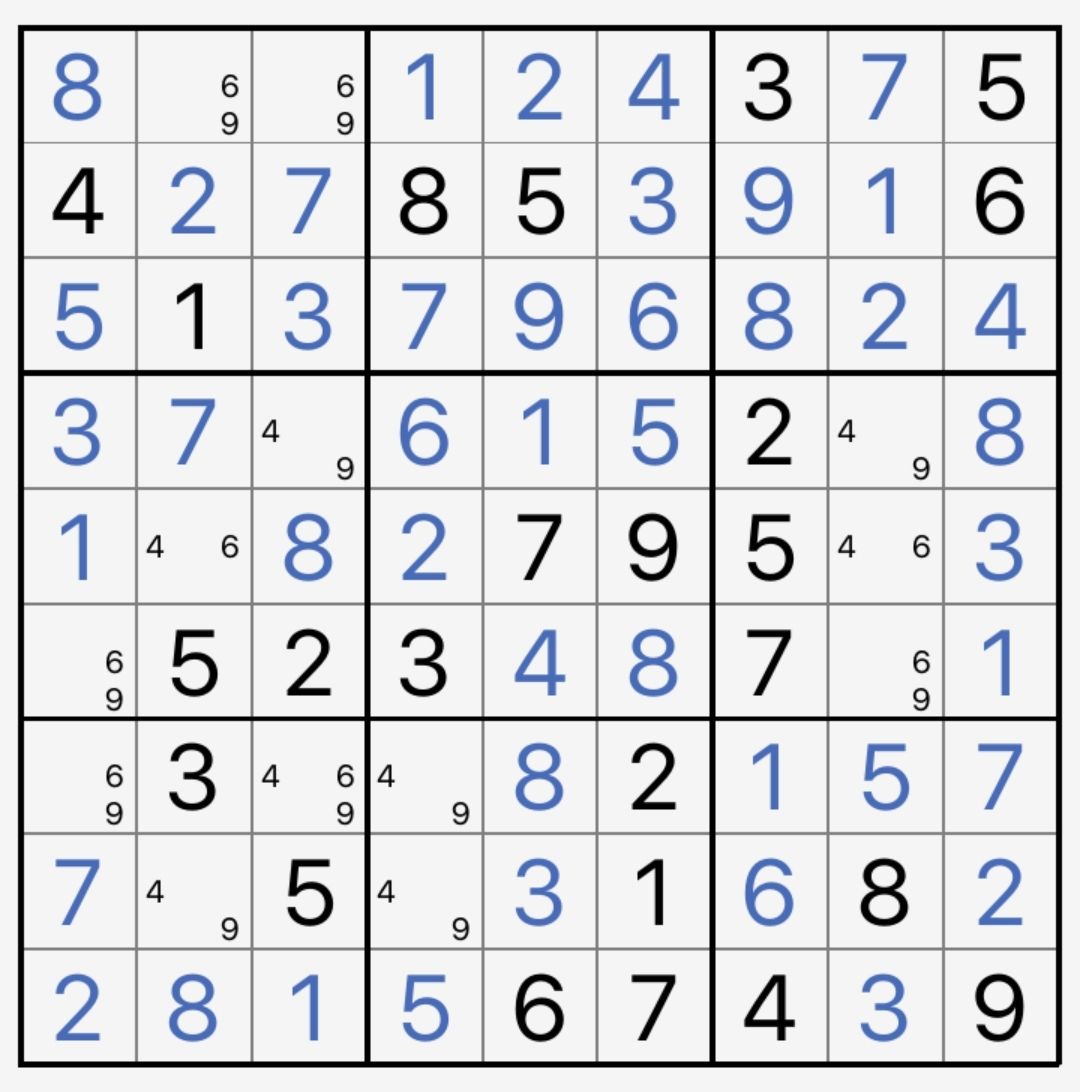
10-2-1 一个BUG+1的盘面
做一个小小的实验：我们把r7c3的9去掉，你会发现，每个单元格有且仅有2种候选数；在任何一个行、列、宫内，每种候选数有且仅有2次出现。此时，无论你试图按何种方法试数，都会在某一处发现矛盾。
现在给出全双值格致死（BUG）的确切定义：
全双值格致死（BUG）是一种不该出现的形式，它同时满足如下两个条件，特别要注意第二条：
（1）未填入数字的每个单元格都是双值格（即有且只有2个候选数的单元格）；
（2）在每一行、列、宫内，所有已现候选数种类都有且仅有两次出现。
反过来说，不满足这两条的结构也就称不上BUG。
我们回到图10-2-1，你会发现去掉r7c3的9之后，剩余的部分恰好满足上面的两个条件。像r7c3(9)这样一旦全部去除就会造成BUG的候选数，我们称之为真数。显然为了避免BUG的出现，所有真数至少有一个成立。
在图10-2-1中，真数只有一个，就是r7c3(9)，于是直接得到r7c3=9。在差点形成BUG的结构中，只有一个真数的情况就称为BUG+1。类似地，有n个真数的情况是BUG+n。
现在来看一个BUG+2的例子，如图10-2-2所示。
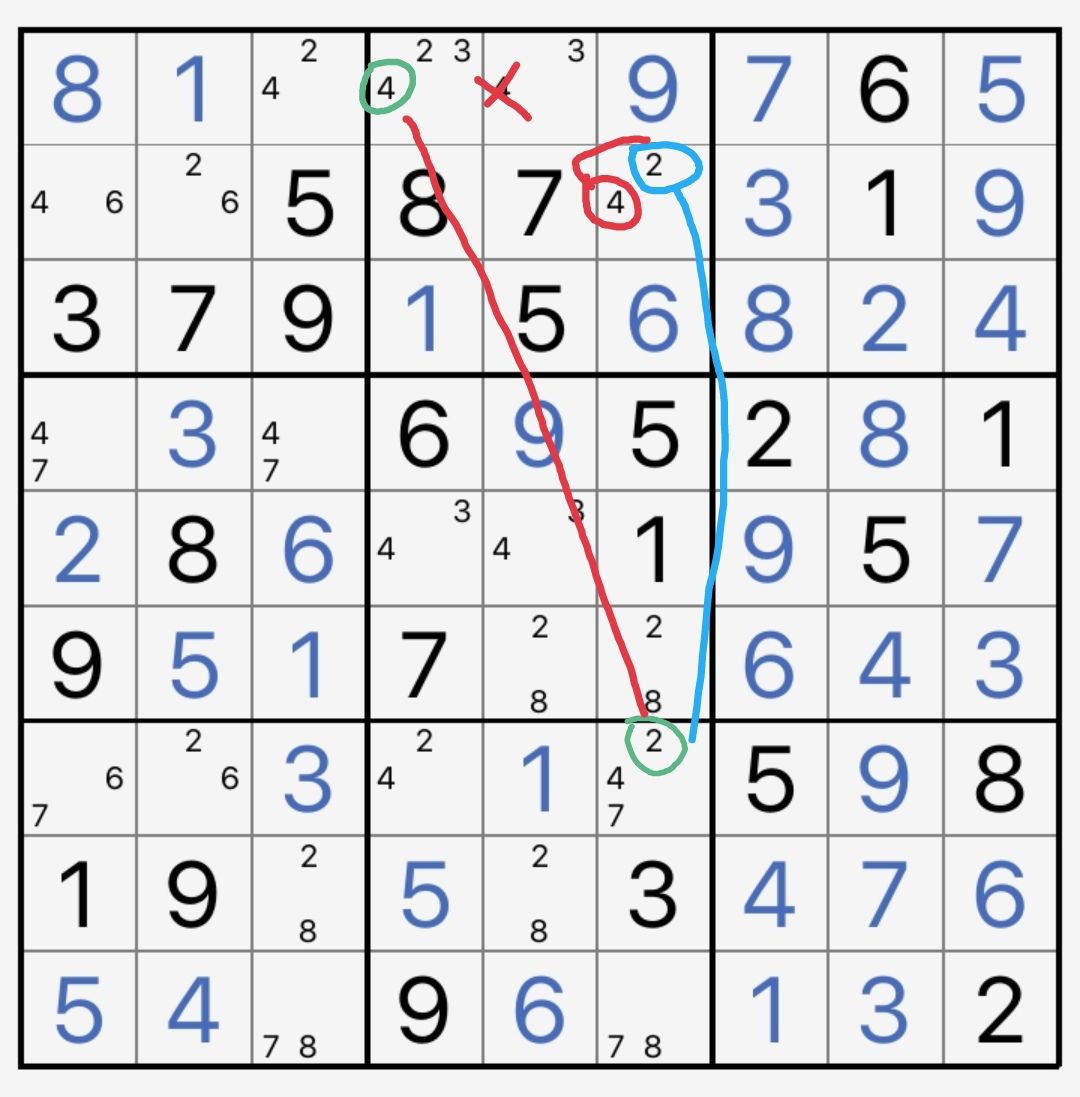
图10-2-2 一个BUG+2的盘面
注意到去除两个绿圈数字后，盘面变成了BUG形式，因此原盘面称为BUG+2。由于真数至少有一个成立，因此两个绿圈数字成强关系。对一端进行延拓，得到链
r1c4(4)=r7c6(2)-r2c6(2=4)
产生删数r1c5<>4。
当然，这题可以更简单地用UR来解，本例只是为了说明BUG+n的使用方法。此外，本例包含了构造的思想，将会在第11章进行介绍。
三、各种Wing
注：除了X-Wing是鱼（非链）以外，其余的Wing都是链的特殊形式。
1. X-Wing（二链列）
X-Wing在本系列的8-1已有讲解。传送门：
2. XY-Wing（双分支匹配）
XY-Wing在难度为3-4星的题目中用途广泛。它的一般形式如图10-3-1所示。通过链的关系，很容易得到
r5c2(6=1)-r5c4(1=4)-r4c5(4=6)
从而产生删数r5c5<>6。
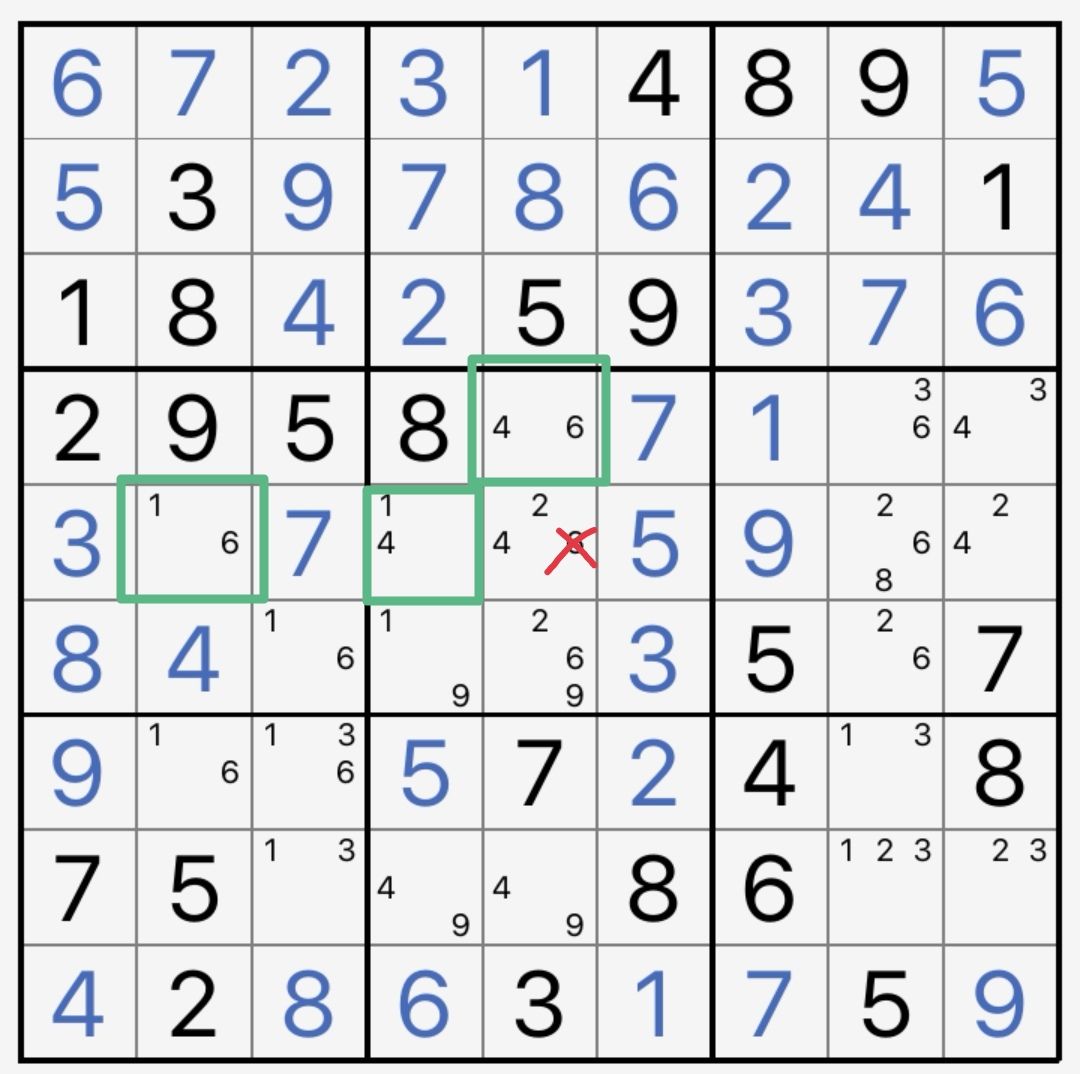
图10-3-1 XY-Wing
作为一种特殊的链，XY-Wing有自己的一种观察方法：
（1）先找到一个含有xy两个候选数的单元格（比如r5c4，此时xy分别是1和4）；
（2）寻找两个单元格，其分别包含候选数xz和yz，并分别与刚才的单元格同区（比如r5c2和r4c5，此时z=6；前者和r5c4同行，后者和r5c4同宫），同区的规定是为了弱链能够相互链接；
（3）则两个z成强关系，可能产生删数。
3. XYZ-Wing（三分支匹配）
XYZ-Wing与XY-Wing相比，只是“中间”的单元格多了一个z值。它的一般形式如图10-3-2所示。
为了理清XYZ-Wing的逻辑，分两种情况讨论：
（1）r5c5<>4，此时r5c5，r4c5和r5c9构成XY-Wing，知r4c5(4)和r5c9(4)至少有一个成立。
（2）r5c5=4。
总之画橙色圆圈的三个4至少一者成立，它们可以共同删除r5c4(4)。
图10-3-2 XYZ-Wing
XYZ-Wing的寻找方式与XY-Wing非常类似，差别只在于第一个单元格必须同时包含xyz三种数字。
值得注意的是，刚才XYZ-Wing的分析包含了毛刺的思想，将会在第12章进行介绍。
4. W-Wing
W-Wing的逻辑与刚才提到的XY-Wing有一些差异，但本质上还是一种特殊的异数链。W-Wing的一般形式见图10-3-3。
根据图示，有链r9c6(8=5)-r7c46(5)=r7c2(5)-r8c2(5=8)，产生关于8的删数。
图10-3-3 W-Wing
W-Wing的一般观察方法如下：
（1）找到两个只包含ab两种候选数的单元格（例如r8c2和r9c6，此时ab代表5和8）；
（2）找到一条关于a（或者b）的强链，强链的两端应分别通过弱链与两个单元格的a（或者b）相连（例如r7上关于5的强链，这条链两端分别通过弱链连接到r8c2和r9c6的5）；
（3）则这两格的b（或者a）成强链（例如这两格的8）。
四、链的常用构型
1. 双强链
在所有链中，以“强弱强”连接的同数链是最基本的形式。因为只包含两条强链，又称为“双强链”。
它的一般形式见图10-4-1，其逻辑和删数在图上一目了然。
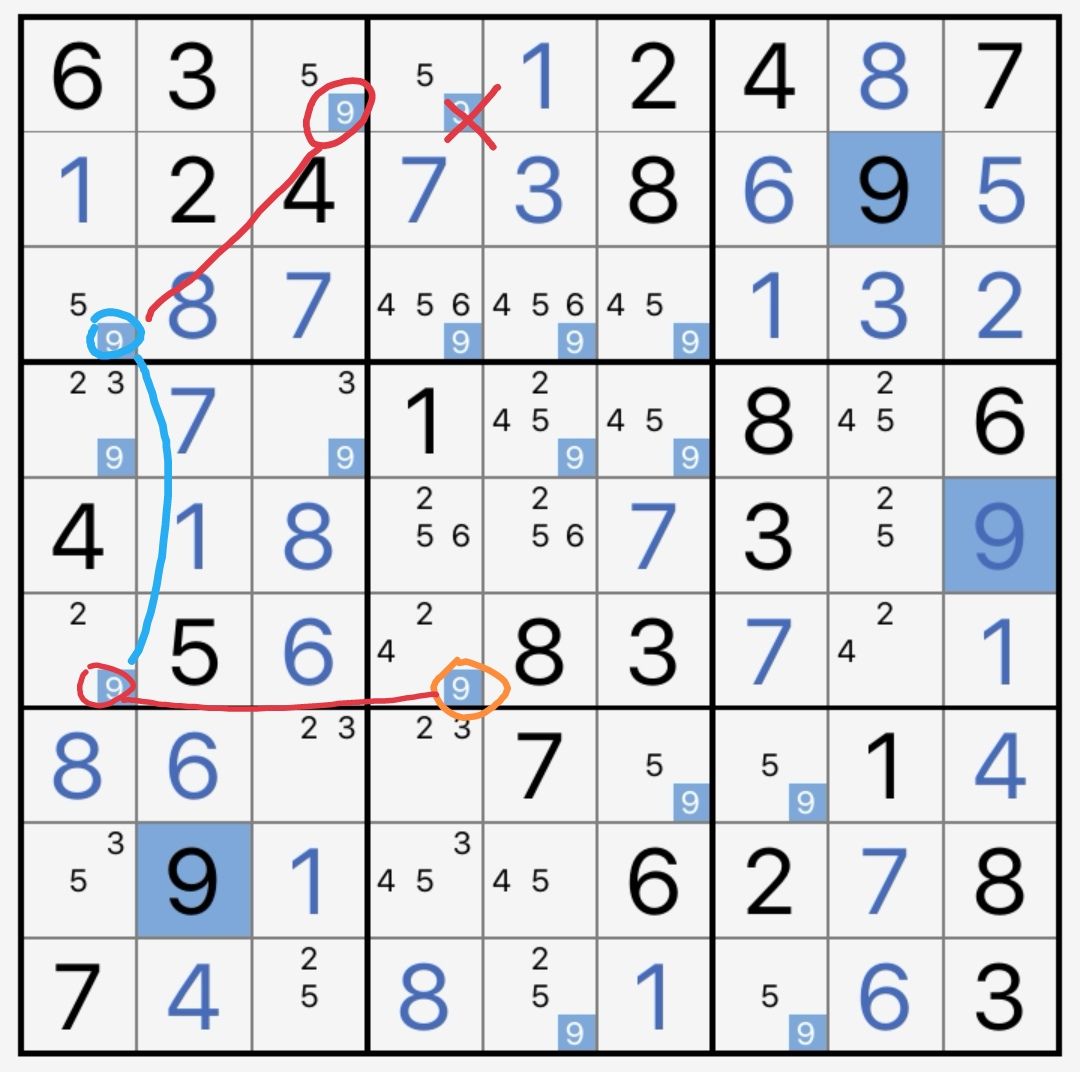
图10-4-1 双强链的一般形式
除了一般形式外，有时两个强链都是水平/竖直的。当它们平行时即构成摩天楼(Skyscraper)，正交（垂直）时构成双线风筝(2-String Kite)。摩天楼和双线风筝是双强链的两种特殊形式，如图10-4-2和10-4-3所示。
图10-4-2 摩天楼
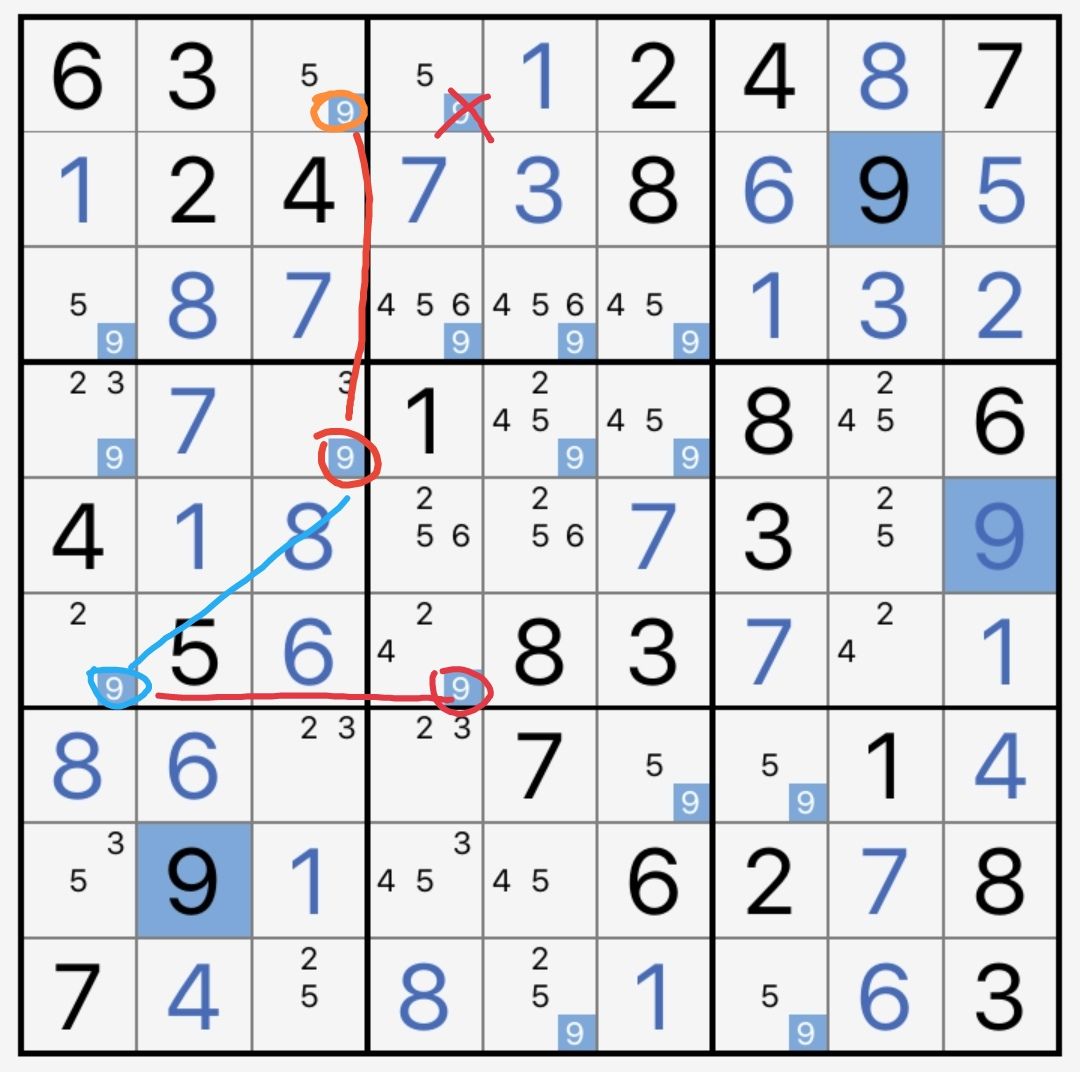
图10-4-3 双线风筝
2. 远程数对
远程数对(Remote Pair)是一种特殊的链，本质是两种候选数的链关系在相同单元格内重叠而形成的特殊情况。
远程数对的一般构型如图10-4-4所示。它的形式是一组只含xy两种候选数的单元格，任取任何一种候选数都可以构成一条单独的链。当然，也可以用袋鼠（数独的包装技巧之一）来理解。总之，远程数对的两端必然填入不同的数字。
在下例中，包含45候选数的单元格就构成这样的远程数对，两端必然一个填4一个填5，总之有删数r4c2<>45。
图10-4-4 远程数对
小结：
小结就在目录里。这些技巧都是数独中常用的方法，不涉及艰深的理论。其至少可用于解决SodoCool关卡模式的4星关，在5星关解题时也可起到辅助和收尾作用。
2.3.4星全通关，写下小心得？
这个游戏其实已经和传统数独有一定区别了，但是效率更高。
在我看来更类似“找区别”，直到所有逻辑通顺，如果实在确定不了的话，试一下会更快。
通关的大致顺序是:（我把一个9宫格叫一区，但是横向一条或者纵向一条也是成立的）
1.先找每个小区里单独的，和相对好找一些的
2.开始逐步排除。第一种情况是如果9个格子里只有2-3个同一行，或者同一列的可能性，那么这整个一行一列都不会再有。
下图是一个变式，因为第
精华
@冬叁月
123 赞
42 回复
EH的数独杂谈#15-3 五星题003
返回传送门：
题目信息：
【SE评级】8.5
【HoDoKu评分】7590
第3题的初盘如图15-3.0.1所示。经四大基本技巧整理，得到如图15-3.0.2的盘面。
Step 1 唯一矩形（UR）
首先可以注意到r23c14四格的候选数26，如图15-3.1所示。它有构成UR的可能，因为6在这四格里只能交叉放置2个。
【删数】r23c4(2)
Step 2 构造链延伸
现在将目光放在图15-3.
@Anthony-XYZ
13 赞
小灰的数独迷你课堂第零讲——总集篇
前言：我个人只是业余数独玩家(我觉得我最多算是益智游戏爱好者)，属于人菜瘾大，水平一般但是喜欢分享（好像也没多少可分享的）。考虑到论坛的活跃程度，估计这篇攻略没多少人看，我就把它作为我的学习笔记来使用吧。想要清楚的教好，自然需要自己先学好。正好看的人不多，我就作为试验性攻略来尝试。如果有玩家看到，欢迎提出宝贵的意见与建议，有想学的技巧（前提我会）或是碎碎念都行。你把它当成聊天灌水帖，有时间的话我也
精华
@咫尺无涯
701 赞
46 回复
EH的数独杂谈#7-2 致命结构（2）- 稍复杂的致命结构
友情提示：本篇是7-1的延伸，但重要性和实用性与7-1等同（甚至更高）。
7-1传送门：
概述传送门：
--------
目录：
一、唯一环（Unique Loop，UL）
1. 唯一环的原理
2. 一些实例
二、拓展矩形（Extended Rectangle，XR）
1. 拓展矩形的原理
2. 一些实例
三、探长致命结构（Borescoper's Deadly Pattern）
1. 3数探长致
@Anthony-XYZ
9 赞
1 回复
EH的数独杂谈#15-1 五星题001
返回传送门：
题目信息：
【SE评级】8.4
【HoDoKu评分】3374
第1题的初盘如图15-1.0.1所示。经四大基本技巧整理，得到如图15-1.0.2的盘面。
Step 1 鳍二链列
如图15-1.1，我们观察4列和9列的候选数4，发现它是以r6c9(4)为鳍的鳍二链列。
【删数】r4c7(4)
Step 2 AIC（异数链）
如图15-1.2，找到如下链：
r2c6(2)=r2c8(8)
@Anthony-XYZ
19 赞
13 回复
玩了一阵子了，从萌新变成新手了，分享一点点入门技巧
我也是个刚玩的萌新，本帖没有提及的技巧代表我也不会。
这款数独分为九个大格，称为九宫。每个宫内又有九个小格子，同一宫、行、列内的数字只能是1-9，不能重复出现。
也就说某一行、列、宫内只能有且必须有一个1到9的数字。
根据这个规则，可以有一个简单的技巧，如下图数字2的分布，我用绿线划掉了2所在的行、列得出数字2在第五宫只能填入红圈位置。
进阶技巧，如下图，数字3的分布，得出数字3在第九宫只能填入黑
@弃疾
74 赞
11 回复
EH的数独杂谈#0 概述
<本帖兼作个人的答疑帖。>
这里是EH数独杂谈系列的导览帖。该系列算半个教程，如果你要从零开始学习数独技巧，可以参看下面的链接：
（1）你游精华区的小灰数独教程系列（涵盖了所有数独技巧里最实用的一批，比较通俗易懂，适合初学者学习）
（2）b站用户 SunnieShine 的“标准数独技巧教程”（视频/专栏/pdf，可能是国内最全面的数独技巧教程，技巧难度从入门到顶尖一应俱全，理论性强）
-----
@Anthony-XYZ
25 赞
22 回复
【攻略/更新中】四星关卡思路提示/51关开始
【3.24已更新至60关】
如标题所言，虽说是攻略但并不直接提供答案，只讲关键节点用什么技巧破局，也欢迎各位数独高手分享提供更精巧的思路。
以防万一事先声明一下：帖主极度排斥在题目正常的情况下用暴力破解，请使用推数穷举解题的玩家止步，此帖是给用技巧解题的数独玩家看的。
我能理解每个人有不同的游戏玩法，但推数穷举在我看来就像是开修改器玩经营类游戏，会令数独失去逻辑推理的乐趣和意义。如果是比赛排名之类
@mowan
13 赞
7 回复
01:13
关掉辅助模式玩
我看你们都是开着辅助玩的，那不就跟玩填空题一样！建议关掉辅助模式，不然你都玩不明白啥叫数独😂😂（个人建议，你喷我那就是我错了）
@User6550533
2 赞
3 回复
燃灯4号：《Sodo Cool》正式发布
你好，我是来自召合网络的燃灯4号，
这里是Azino同学自《2048清》之后开发的个人作品《Sodo Cool》。
《Sodo Cool》的1-2星难度适合”数独入门之后“的玩家体验，3星以上适合高手，5星难度适合…超级高手-_-
（燃灯我自己弱爆了，3星第一关还没过…Azino他也卡在3星…）
那为什么现在才挂上召合的厂牌呢？
燃灯4号：
”因为之前的版本，游戏体验不够优秀哇……“
现在！
《S
官方
@燃小灯
118 赞
36 回复