推理小技巧No.4:【最小占格数】
今天带来的是95%以上的关卡都会用到的推理小技巧——【最小占格数】,首先我们来看下图:

数字线索是4/2,也就是一共四个蓝格,被分成了两段,但此时并不知道蓝格是怎么分布的,那么该如何打开局面呢?
推理步骤1:首先,4个蓝格既然要被分成两段。那么,这4个蓝格中间一定有空白格。空白格可能多、可能少,但是,至少有一个空白格才能分成两段:
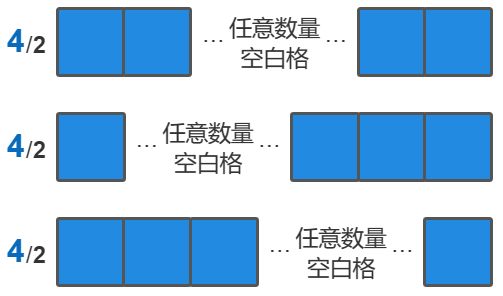
推理步骤2:因此,上图中的“任意数量空白格”,最小就是1。那么,再加上总共有4个蓝格,所以4/2线索占用的长度,至少是:4+1=5格,无论4/2的分布是什么样的,它都至少需要占用五个格子的长度:
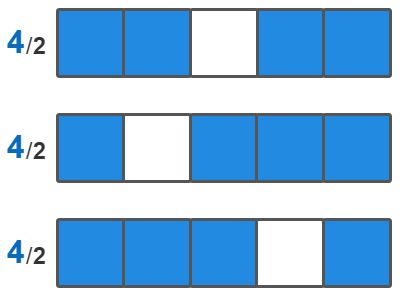
推理步骤3:5格已经是该线索最短的长度了,不可能短于5格。而如果这一行的总长度,恰好等于5格,这意味着,最左侧和最右侧,一定是蓝格。否则,一旦边缘有一个空白格,那么这行的可用长度只剩4格了,是放不下4/2这样的线索的:

推理步骤4:这里有一个简单的公式可以使用,是关于计算一个线索的最小占格数的,公式如下:

这个看似是个公式,其实在实际应用中非常简单,其含义就是蓝格数量,再加上每个分段之间只有1个空格的数量 。
例如线索【3/2】,它的最小占格数就 = 3 + 2 - 1 = 4格(也就是3个蓝格之间,至少有一个空白格)
再例如线索【4/3】,它的最小占格数就 = 4 + 3 - 1 = 6格(也就是4个蓝格之间,至少有两个空白格)
————————分割线————————
该技巧的应用很广泛,并且还可以拓展到更多的情况,后续有机会我会把拓展攻略也分享一下~


