一帖搞定！5个骰子游戏的最优策略（答案在最下面）

一、不考虑对手（双盲）

5>4+1>3+2>3+1+1>2+2+1>1+1+1+1+1>2+1+1+1

分别记得分为7654321（这样记分计算期望应该是合理的吧，如果不对还请大佬指出）

以下是概率树状图（原图太大发不出，只能拆成两半）

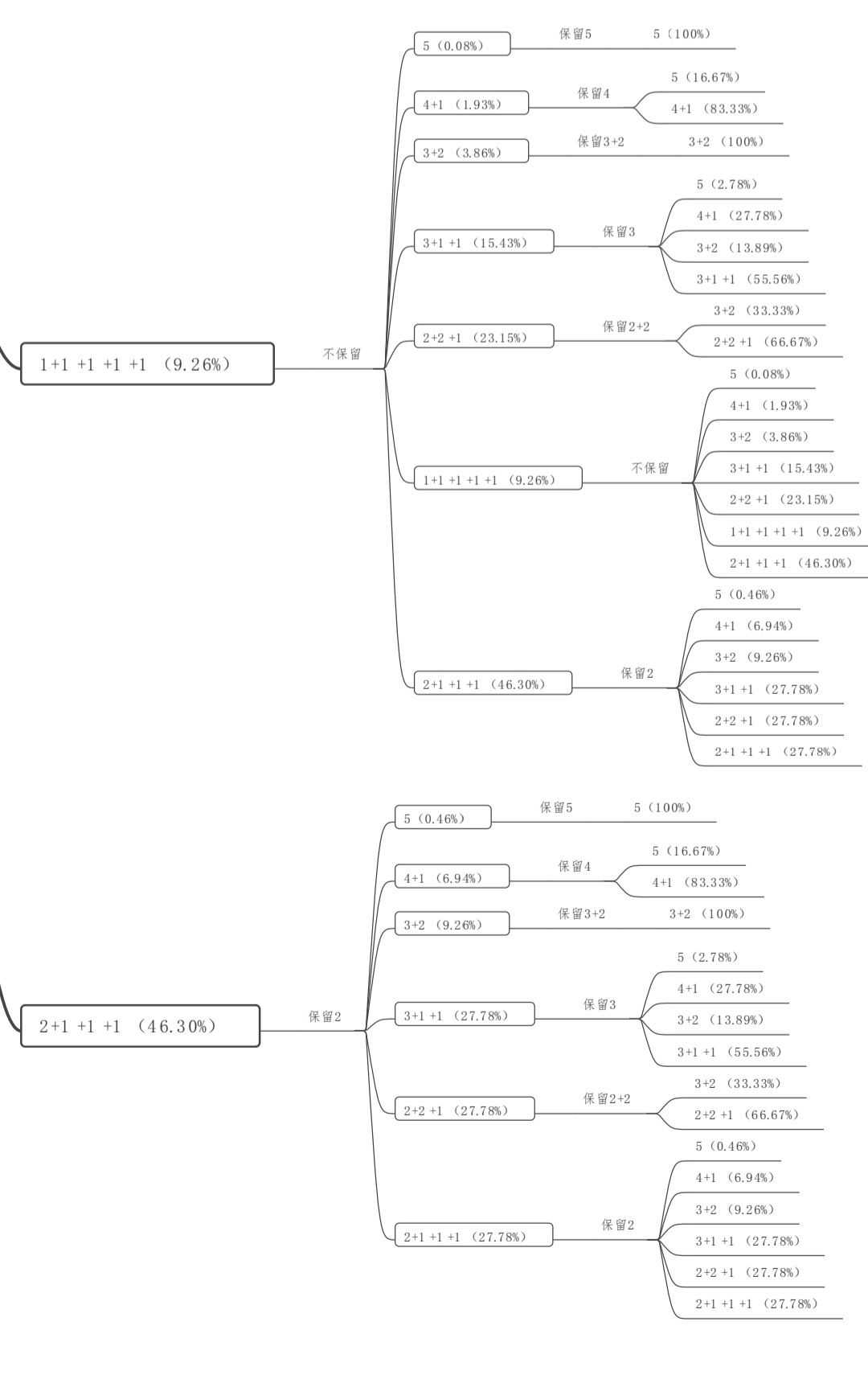
1+1+1+1+1明明那么稀有，为什么是倒数第二菜的……

不过如果1+1+1+1+1真的是高分牌型那我可就要算死了

需要进行抉择的有三种情况：

（1）3+2 如果保留3，期望得分4.78，比原来低

所以应保留3+2

（2）2+2+1如果保留2+2，期望得分3.67；保留2，期望得分3.13；不保留，期望得分2.27所以应保留2+2

（由于全留相对于保留2+2必然是劣势策略，因此虽然不能直接看出全留和保留2以及不保留的优劣，我们也不用考虑全留的情况）

（3）2+1+1+1 可保留2或不保留，应保留2

但是我们并不能因此就认为遇到2+2+1就一定要保留2+2，通过后续计算我们会发现，第一次和第二次出2+2+1和3+2的选择都是不一样的。

（众所周知，面对概率你的直觉绝对会骗你）

不过由于不保留时概率提升的牌型无论在当前得分还是后续得分上都是劣势的，所以除了1+1+1+1+1，无论什么时候不保留的策略都可以被剔除。

为了让树状图更小一些，对于第二次投掷的结果，我在图中只画了最优策略。

所以，实际上不同的策略仅仅是：在第一次投掷后遇3+2有两种策略，遇2+2+1有两种策略，共4种。

那么，究竟哪种策略最好呢？

经过坚苦卓绝的计算，发现：

（1） 第一次投出3+2 如果保留3，期望得分5.26；如果保留3+2，期望得分5

（2） 第一次投出2+2+1 如果保留2+2，期望得分4.11；如果保留2，期望得分4.14

看，如果是第二次投出2+2+1，保留2+2更好，但如果第一次投出2+2+1，就是保留2更好了。第一次和第二次投出3+2时策略的选择也是不一样的。

所以，我们应采取如下策略，以得到最高期望得分4.33（介于3+2和3+1+1之间）

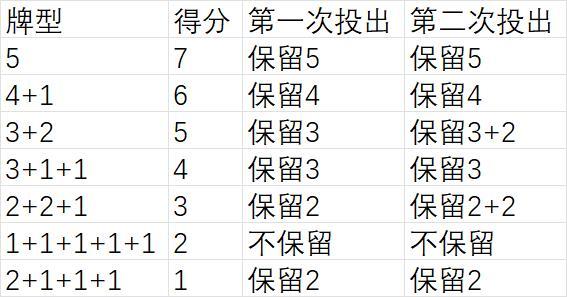
如果投三次骰子还没出3个相同，你就该反思一下最近做了什么掉欧气的事了……

后续会更新考虑对手的策略