减法器和乘法器的设计思路。

修改于2021/07/11593 浏览攻略

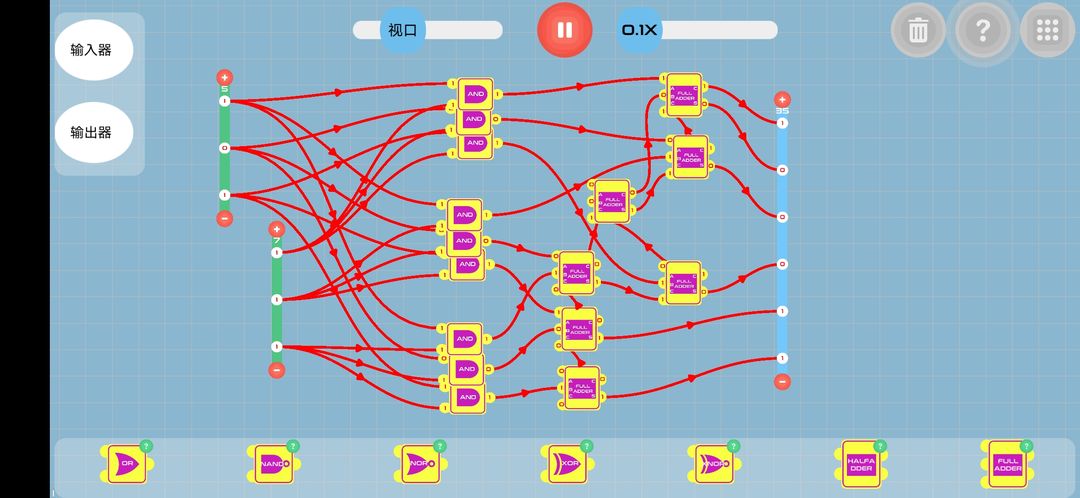
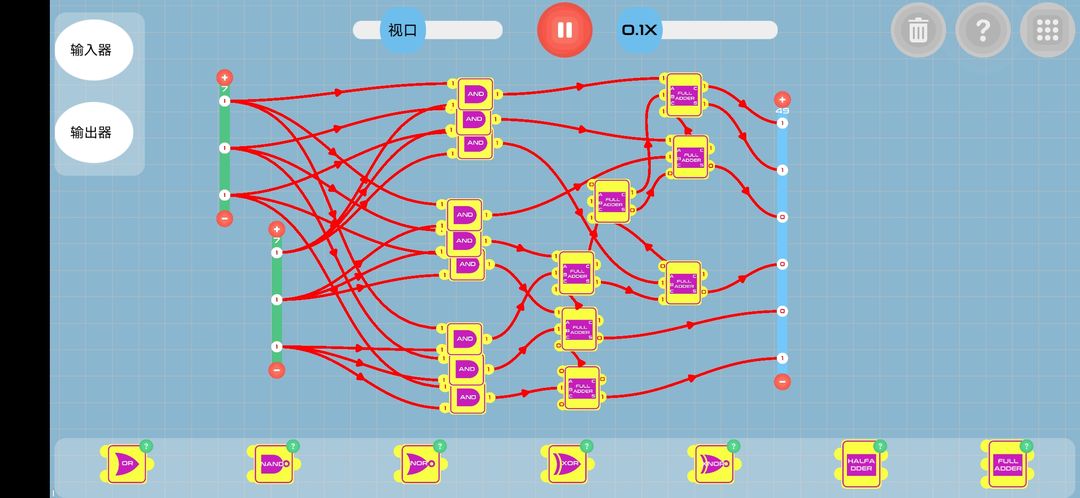
乘法器

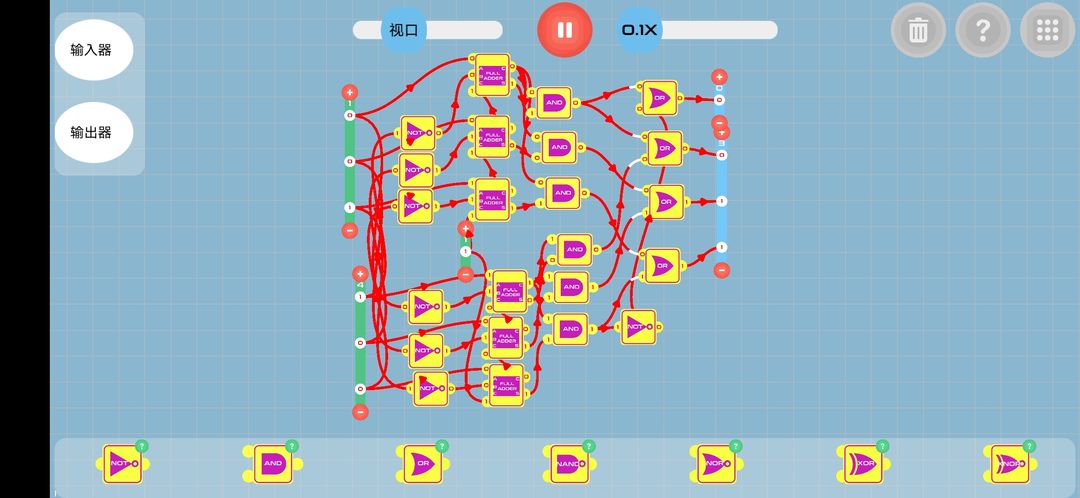
减法器

一、乘法器讲解：

值得注意的是，与门本身就有乘法的功能

并且与门本身就能计算1位乘法。

因为与门的真值表

00 0→0*0=0

10 0→1*0=0

01 0→0*1=0

11 1→1*1=1

那么我们要怎么解决位数高一些的乘法？

我们先看二进制竖式是怎么计算高位乘法的。

比如一个7*7的二进制竖式：(从左往右1248...)

111

111 *

--------

111 第一组与门(先看完下一段再回来看)

0111 第二组与门(同上)

00111 + 第三组与门(同上)

--------

100011

图一中从下往上有三组与门(一组三个)，从下往上的第一组与门到第三组与门就是与竖式中写的对应的。

而后面的全加器只是为了完成

111+0111+00111

这样就根据二进制的乘法竖式设计出了乘法器。

二、减法器讲解：

对被减数反码后补码，减数再加上上一步操作的结果

例1 比如101-010=011

对010反码→101

再对101补码→110(相当于给101+001)

最后101+110=1011(最高位的1表示正号)所以这一步的答案应该是1 011也就是正011。

但是反码补码虽好，却不能用小的数减大的数。

例2 比如001-100=0 011(最高位的0表示负号)

按照之前对100反码补码得到100

而001+100=0 101明显不正确。

这样就需要判断大小了。

值得注意的是，在例1中，是大数减小数，得到的符号位是1；而在例2中，是小数减大数，得到的符号位是0。

也就是说，大数减小数得到的符号位和差都是对的；而小数减大数得到的符号位是对的，差是不对的。

所以假设有两个二进制数a、b，我们不知道它们的大小，但是我们要计算a-b的值。所以我们就可以同时计算a-b和b-a，根据减出来的符号位来判断a、b的大小，然后获取大数减小数的答案，最后补上差的正负号即可。

比如我们要计算a-b，所以我们同时计算a-b和b-a。

①如果a-b的符号位是1并且b-a的符号位是0，那么我们就获取a-b的差为结果，并给这个结果冠以正号1。

②如果a-b的符号位是0并且b-a的符号位是1，那么我们就获取b-a的差为结果，并给这个结果冠以负号0。

这样我们就解决了减法器的小的数减大的数的问题。

但尚未解决负数减负数和负数减正数以及正数减负数的问题。

欢迎大家讨论，如果有问题可以询问或者反馈，我会及时更正。

确定不给我挂精贴吗？ [嗒啦啦2_起了杀心]

猜你想搜

与门乘法器设计

与门测试

9.3

前往论坛