#徽州攻略#关于徽商市场占有率和垄断 · 修改稿
修改于2021/07/051.1 万浏览攻略
关于徽商市场占有率和垄断 · 修改稿
---------------------------------------------
一种基础物资只能由特定的某一家徽商销售。
文章讨论的结果,亦注明在摘要的末尾处,姐妹们可在摘要的末尾看到计算结果。
---------------------------------------------
文章系多人合作完成,故将参与作者昵称和游戏ID列举如下(排名不分先后):
红衣m520snf34m5,寻藏mjb54jduret,鱼鱼鱼mlcae7jxtkz,国民仙女mfr1m3f85ch,夕溟wawbbyyda99,苏晚落mlcaxb8d2pe,长安归故里m8m03744xnp,SLUMP m6ulyatuenu
---------------------------------------------
摘要:
徽商经营玩法是江南百景图徽州府的特有玩法。在议事堂内,玩家可以进行招募徽商并委派徽商售出大量资源,从而可以换取大量铜钱、家族资金和徽州资源金箔。其中,徽商所销售的物资量会被计入市场总量之中,一旦徽商销售物资量达到市场总量的90%之后,即可进入“垄断”状态,从而获取更多的收益,并且解锁后续的徽州特产物资—笔墨纸砚的销售权,从而赚取更大的利益。文章研究的方向是,不考虑物资种类的情况下的一般垄断规律模型,从而为玩家提供相对稳健的垄断方案。
第一步,文章根据收集到的相关资料,建立市场自发增长的分段函数模型。
第二步,文章从徽商市场占有率的定义入手,结合第一步得到的市场自发增长模型,计算得到徽商市场达到垄断所需要的总资源量和时间的关系式,即垄断的基本模型。
第三步,在徽商垄断的基本模型之上,得出徽商垄断所需时间和每日平均销售量的关系式,即时间公式和平均量公式。通过这两个公式可以看出,徽商需要多天慢慢培养,不建议操之过急。
第四步,通过MATLAB对上述的模型进行数学分析,我们便可以得出徽商垄断的最佳方案。在这里,各位姐妹可能对最佳方案的定义不尽相同,为了满足不同姐妹的需求,我们将分别取5、7、10、15、20、25天内达到垄断所需的每日平均销售量(如表0-1所示);以及每日平均销售量在400、600、1000、1400、1600、2000、2400、2600、3000、3400、3600、4000的时候徽商达到垄断所需要的时间(如表0-2所示),以供姐妹们参考。如果姐妹们要求佛系的话,可以在表0-2取每日销售量在2000或1000以下的数据作参考;如果姐妹们要求快速的话,可以在表0-1取5或7天内达到垄断的相应数据作参考。结论如下:
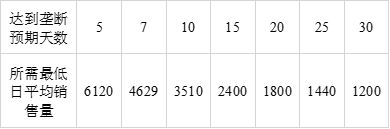
表0-1 所需天数-日均销售量对照表(肝帝用)
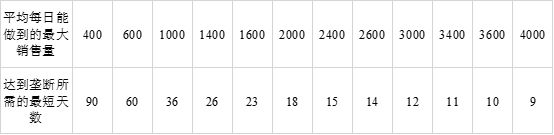
表0-2 日均销售量-所需天数对照表(佛系用)
作者水平有限,文中如有错误,欢迎姐妹们多加批评指正。
关键词:徽州攻略,徽州府,徽商,垄断,市场模型,分段函数,高斯取整函数
正文:
一、 问题重述
徽商经营玩法是江南百景图徽州府的特有玩法。在议事堂内,玩家可以进行招募徽商并委派徽商售出大量资源,从而可以换取大量铜钱、家族资金和徽州资源金箔。其中,徽商所销售的物资量会被计入市场总量之中,一旦徽商销售物资量达到市场总量的90%之后,即可进入“垄断”状态,从而获取更多的收益,并且解锁后续的徽州特产物资—笔墨纸砚的销售权,从而赚取更大的利益。
本题要求用数学建模的方法分析以下问题:
在不考虑物资种类的前提下,给玩家提供相对稳健的垄断方案。
二、 问题分析
初期,当建设好家祠和议事堂之后,在议事堂之内,我们就可以解锁徽商。在徽商处,初期,我们可以销售竹子、茶叶、桐油、生漆这四个基础物资。之后的讨论都是基于对四中基础物资的销售。销售的物资就可以成为流通进入市场的一部分。
由此,我们就可以引入市场总量的概念。市场总量,就是指流入市场的某种资源的总的量的大小。市场总量由三部分组成,即初始市场总量、徽商资源销售总量和其他渠道销售量。显然,市场总量的大小为这三部分的量相加之和。根据游戏实践,和对于论坛攻略的参考,我们便可以得出市场自发增长的规律模型。之前,由于徽商玩法实践经验不足,认为垄断之前市场的增长量,一直是每过一天增长100固定不变,并且没有上限的。而实际上,参考了更多的资料之后,我们发现,当市场中非徽商占有量达到4000的时候,便不再自发增长。于是所做的市场自发增长模型中,当垄断所需的时间超过11天的时候,模型拟合错误,于是根据现在所了解的市场的增长量规律按照相同思路重新建立模型。
由此,我们可以引入市场占有率的概念。我们可以定义某一家徽商该种物资的销售量与市场总量的百分比为该徽商的该种物资市场占有率,即如下面的公式所示:

由此,我们可以引入垄断的概念。根据官方规则,我们可以定义,当某家徽商某种物资的市场占有率超过90%的时候,就可以称他们在这个物资市场进入了垄断状态。很显然,由以上的定义,我们可以知道,正如辛夷等版主所言,最好四个徽商家族,每一个徽商家族都分别只销售四中基础物资中的某一种物资,这样就可以减小使徽商达到垄断状态的难度。在之后的讨论中,我们也默认每一种基础物资只由特定的某一家徽商销售,以期简化问题,减小讨论的难度。
由垄断的概念,我们便可以根据市场占有率的定义式,来得到达到垄断时所需时间和最小物资总量的关系式。这个关系式就是基本垄断模型关系式。
基于基本模型垄断关系式,我们可以引入每日日平均最小销售量的概念,从而得出每日平均最小销售量和从开始经营到达到垄断状态所消耗的时间的数量关系式,即时间公式和平均量公式。时间公式就是达到垄断状态所消耗的时间关于每日平均最小销售量的函数关系式;而平均量公式就是每日平均最小销售量关于达到垄断状态所消耗的时间的函数关系式。
基于上述两个函数关系式,我们便可以利用MATLAB数学工具进行快速计算,从而得到二者的函数关系图和所需要的数据表。
三、 条件假设
a. 本文讨论仅限于基础物资的垄断。
b. 基础物资的市场自发增长模型成立。
c. 每一种基础物资只由特定的某一家徽商销售。
d. 只要到达垄断状态,就可以解锁后续的游戏玩法,同时,后续的游戏玩法一旦解锁,之后就永远不会重新锁定。
四、符号说明

显然,这五个量均为正整数。
五、模型的建立
1、非徽商市场占有量增长模型
根据游戏经验和攻略参考,非徽商市场占有量是初始市场总量和其他渠道进入市场的销售量之和。最初始的时候,非徽商市场占有量为3000,之后,若未达到垄断,则每天增长100,直至增长到4000为止,不再增长。于是有:
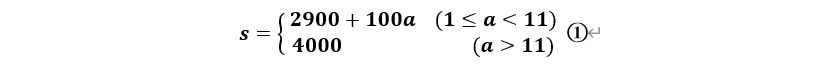
2、基本垄断模型
由徽商规则中的相关定义,我们可以将垄断抽象成如下的数学模型:
令自徽商开始进行某种基础资源的销售的日期为第一日,设在第a日达成垄断,所需要销售资源的总量为x,则有:
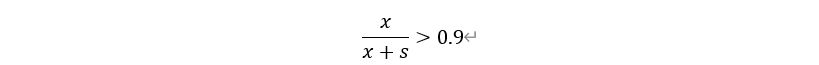
将分式化为整式得:
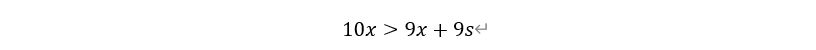
解得:
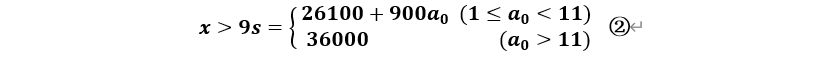
3、时间公式和平均量公式
以下模型都是基于对x的赋值,即可得③式:
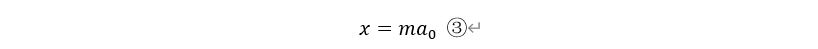
将③代入②,则:
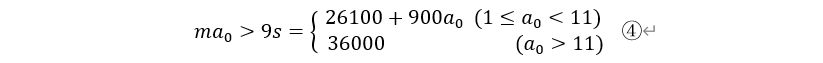
很显然,对于时间公式的计算可知,此时,由于约束条件a0的影响,对于时间公式模型的求解必须根据a0限制范围的不同,进行分类讨论,即:

显然,此时
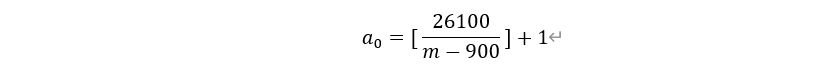
(注:[x]为不超过x的最大整数,下同。)
而此时有临界条件:
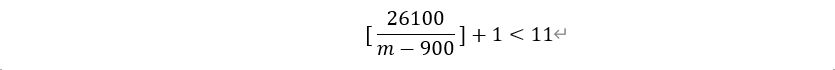
即
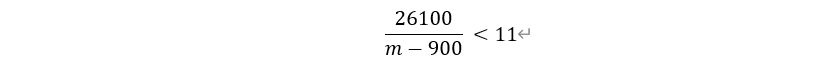
即
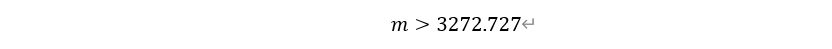
在计算中,小数部分对于计算结果无影响,故此时不舍去小数部分。
2)当a_0≥11时,显然,1≤m≤3272.727,此时:
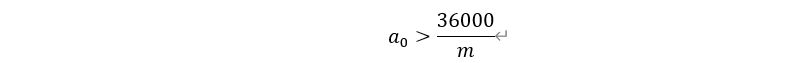
即
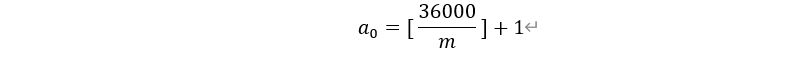
综上所述,我们可以求得时间公式⑤如下:
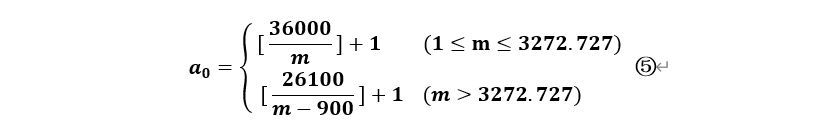
而若我们对于④式做出另一种变换,则可以得到如下的平均量公式⑥:

即
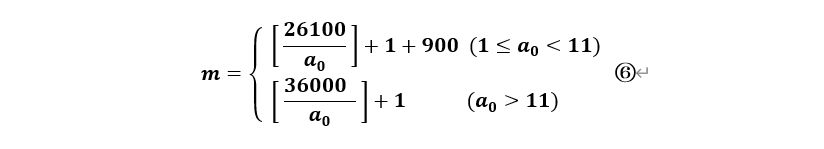
六、模型求解
通过所求得到的时间公式⑤和平均量公式⑥,我们可以初步判断两个函数的单调性。通过对于上述求解过程的分析,我们发现,总体上,达到垄断所需要的最小天数a_0和最小日平均销售量m相互之间呈负相关关系,无论谁是自变量,谁是因变量。而根据推导过程分析,可以发现,在单调性方面,两个函数整体上都是单调不递增函数。如此,我们可以选定自变量的范围加以分析。
然而,根据得出的解析式,我们发现,两个函数中都存在高斯取整函数f(x)=[x],于是,显然,难以用手工方法进行精确的分析。于是,文章采用MATLAB编码求解的方法,以期提高分析的精确程度和减小手工工作量。
对于时间公式进行函数分析的时候,为了用最少的数据模拟游戏环境,根据游戏中徽商的交易玩法特点,以及玩家生产力现实条件,初步地,我们可以选取自变量m取值范围[200, 5000],首数为200,以200为取值步长在取值范围内进行取值,输出数据表如表6-1所示:

表6-1 时间公式输出值表
同时亦可得到函数图像,输出图像如图6-2所示:
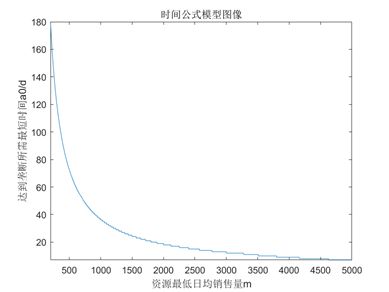
图6-2 时间公式模型函数图像
对于平均量公式进行函数分析的时候,初步地,我们发现,让徽商在短时间之内达到垄断状态,几乎不可能通过正常的游戏方式实现。因此,为模拟玩家需求,我们可以将取值范围的下界定为3,上界定为30。于是,初步地,我们可以选取自变量t取值范围[3,30],首数为3,以1为取值步长在取值范围内进行取值,输出数据表如表6-3所示:

表6-3 平均量公式输出值表
同时函数图像如图6-4所示:
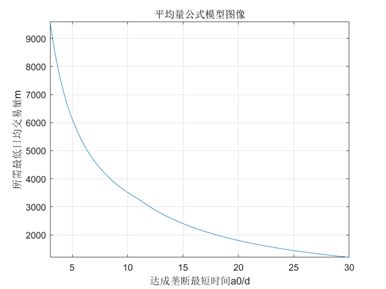
图6-4 平均量公式模型函数图像
七、结论
通过对垄断模型、时间公式模型和平均量公式模型的研究,可以发现,如果要使徽商在一天之内达到垄断状态,那么他就需要销售27000个物资。显然,让徽商短时间之内达到垄断状态,需要大量的山笋和极高的家族等级,而这也需要大量的资源、铜钱和补天石;除此之外,这个销售量也完全超过了大部分玩家五个城的总的库容量和总的生产力水平,几乎不可能通过正常的游戏手段实现。
于是,便有了对相对稳健的方法的探讨。这种探讨,涉及人物选择、资源选择等一系列方方面面,许多版主在此已有了比较深入的探讨,因此本文不再赘述。而对于相对稳健的方法的探讨,每个玩家根据自己的实际情况,又会有着自己不同的见解。于是,根据徽商贸易规则、游戏经验和相关的攻略,我们可以在所得到的两个输出值表中的数据进行再筛选,仅保留重要的节点数据。于是,最终得出数据,如表7-1、表7-2所示:

表7-1 所需天数-日均销售量对照表(肝帝用)

表7-2 日均销售量-所需天数对照表(佛系用)
于是,如果姐妹们要求佛系的话,可以在表7-2取每日销售量在2000或1000以下的数据作参考;如果姐妹们要求快速的话,可以在表7-1取5或7天内达到垄断的相应数据作参考。如果需要更加详细的数据,则可以通过模型求解中所总结的数据表进行对照,或根据时间公式⑤和平均量公式⑥自行求解计算。
参考文献
[1] 江南百景图.【江南百景图】1.5.0徽州府新版本内容解析[EB/OL].https://www.taptap.com/topic/18514725,2021-06-26.
[2] 辛夷.【徽州】快速了解徽商玩法[EB/OL].https://www.taptap.com/topic/18546181,2021-06-30.
[3] 孖㺭.#徽州攻略#徽商小提示[EB/OL].https://www.taptap.com/topic/18548690,2021-06-30.
[4] 声声慢.#徽州攻略#,十分钟开启徽商新玩法(注意十分钟开启)[EB/OL].https://www.taptap.com/topic/18547653,2021-06-30.
[5] 笔墨写春秋.徽商玩法粗解(萌新向)[EB/OL].https://www.taptap.com/topic/18579573,2021-07-03.
[6] sssunny0607.关于徽商垄断及市场的每日增长[EB/OL].https://weibo.com/3227297644/Kn320CqbE?from=page_1005053227297644_profile&wvr=6&mod=weibotime&type=comment#_rnd1625358340689,2021-07-03.
[7] 大彪哥.关于徽商垄断的官方计算方式[EB/OL].https://www.taptap.com/topic/18584795,2021-07-04.
[8] 轩蝶.想请教一下关于徽商的问题[EB/OL].https://www.taptap.com/topic/18583020,2021-07-04.
附录(可跳过):
一、 时间公式
1. MATLAB程序脚本
clear,clc
fun=@(m)ceil(36000./m).*(m>=1&m<=3272.727)+...
ceil(26100./(m-900)).*(m>3272.727)
%计算函数值
m=200:200:5000
a0=fun(m)
%绘制函数图形
fplot(fun,[200 5000])
2. MATLAB输出结果
fun=
包含以下值的 function_handle:
@(m)ceil(36000./m).*(m>=1&m<=3272.727)+ceil(26100./(m-900)).*(m>3272.727)
m=
列 1 至11
200 400 600 800 1000 1200 1400 1600 1800 2000 2200
列 12 至22
2400 2600 2800 3000 3200 3400 3600 3800 4000 4200 4400
列 23 至25
4600 4800 5000
a0=
列 1 至23
180 90 60 45 36 30 26 23 20 18 17 15 14 13 12 12 11 10 9 9 8 8 8
列 24 至25
7 7

二、 平均量公式
1. MATLAB程序脚本
clear,clc
fun=@(a0)(ceil(26100./a0)+900).*(a0>=1&a0<11)+...
ceil(36000./a0).*(a0>=11)
%计算函数值
a0=3:1:30
m=fun(a0)
%绘制函数图形
fplot(fun,[3 30])
2. MATLAB输出结果
fun =
包含以下值的function_handle:
@(a0)(ceil(26100./a0)+900).*(a0>=1&a0<11)+ceil(36000./a0).*(a0>=11)
a0 =
列 1 至 22
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
列 23 至 28
25 26 27 28 29 30
m =
列 1 至 11
9600 7425 6120 5250 4629 4163 3800 3510 3273 3000 2770
列 12 至 22
2572 2400 2250 2118 2000 1895 1800 1715 1637 1566 1500
列 23 至 28
1440 1385 1334 1286 1242 1200



