伤害机制实测推论全过程-风月攻略组

精华修改于2019/10/132278 浏览攻略

结论放前面好了

伤害波动：

首先食物语的伤害是波动的。有的游戏浮动会与敌方血量挂钩，所以为了确定这个情况，录了一个视频。

https://tieba.baidu.com/p/6287351045?pid=127816626845&cid=0&red_tag=0592473914#127816626845

可以看到并不是随血量下降而上升来波动的。所以得到假定公式

平均伤害*(1±伤害波动率)

这里先假定伤害波动率为10%

即

平均伤害*(1±10%)=实际伤害

基础伤害公式：

由于伤害受防御影响，我们直接选择鸡丝测试最基础的伤害公式是否在食物语中也通用。

攻击*倍率*（1+攻击加成）*（1+暴伤）

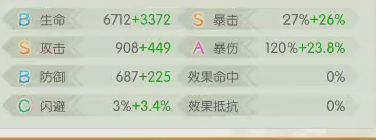
鸡丝测试面板

鸡丝无暴击，金身

理论伤害678*330%=2237.4 实际伤害2188 伤害波动范围内

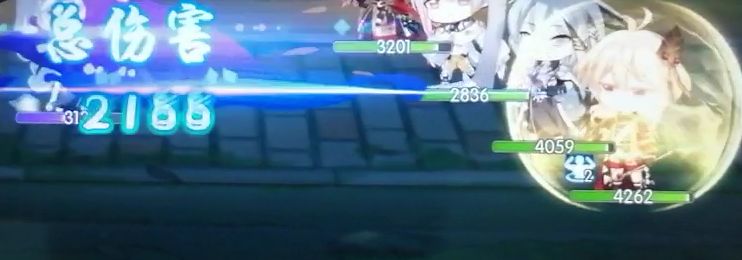
鸡丝无暴击，金身，减低防御

理论伤害678*330%=2237.4 实际伤害2217 减低防御上限100%

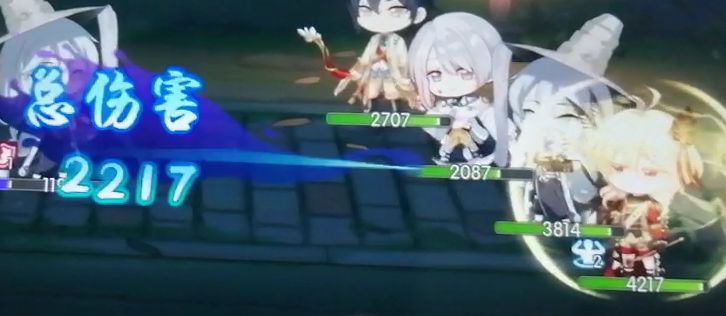
鸡丝无暴击，金身，攻击加成

理论伤害678*330%*1.25=2796.75 实际伤害2736 伤害波动范围内

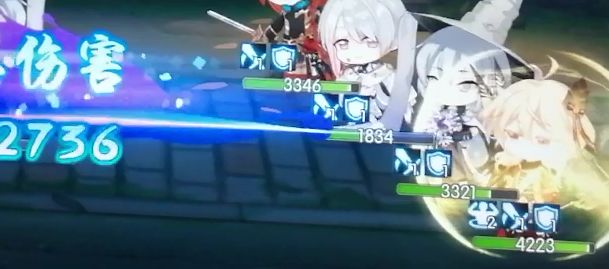
鸡丝暴击，金身

理论伤害678*330%*1.78=3982.572 实际伤害3887 伤害波动范围内

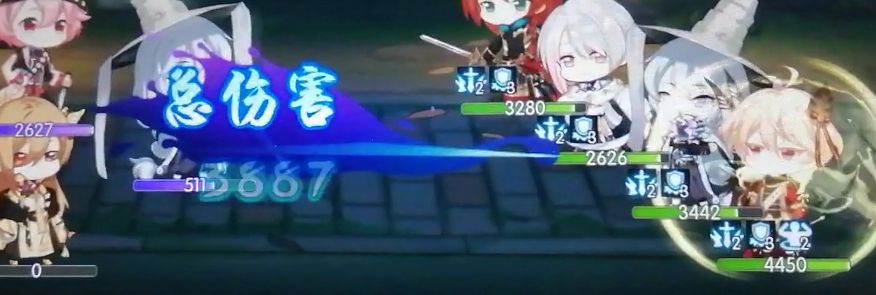
即

攻击*倍率*（1+攻击加成）*（1+暴伤）

在本次测试中成立。

防御&穿透：

虽然我们知道降低/穿透防御的上限是100%，但是我们还不能确定穿透与防御的叠加关系是相加还是相乘。

所以我们用龙井测试一下

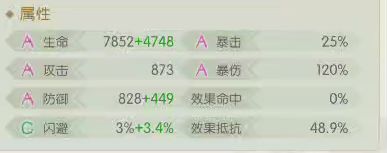
满级龙井四花无暴击，减低防御伤害测试。

根据之前假设的公式

理论伤害

=攻击*(1+攻击加成)*倍率*（1+暴伤）

=1090*220%

= 2398

实际伤害2350

73级龙井零花无暴击，减低防御伤害测试。

理论伤害

=攻击*(1+攻击加成)*倍率*（1+暴伤）

=930*220%

= 2046

实际伤害 1691 超过伤害波动值

31级龙井二花无暴击，减低防御伤害测试。

理论伤害

=攻击*(1+攻击加成)*倍率*（1+暴伤）

=409*220%

=899.8

实际伤害 934 符合波动值

龙井零花30%穿透，一花45%穿透，四花60%穿透。如果是乘法则一花和四花的伤害数值不应该符合伤害波动，更不可能高于理论伤害。

所以认为是穿透与防御降低计算为加法

即

防御*防御系数*（1-（穿透+防御降低））

如果穿透+防御降低=100%，则

防御*防御系数*（1-（穿透+防御降低））= 1

另外由于考虑到实际伤害没有打出1，或者0。所以伤害公式不能假定为

攻击*(1+攻击加成)*倍率*（1+暴伤）- 防御*防御系数*（1-（穿透+防御降低））

=实际伤害

那么我们假定公式为

攻击*(1+攻击加成)*倍率*（1+暴伤）* 防御*防御系数*（1-（穿透+防御降低））*(1±10%)=实际伤害

防御系数函数图：

那么防御系数是多少呢，我们需要绘制防御与伤害率的函数图，才能假定函数。

利用厨艺大赛可以看到对面防御这一点，我们可以做到。

一品锅二技能，无暴击无加成。理论值如下：1246*190%=2,367.4

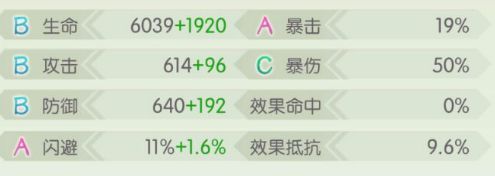
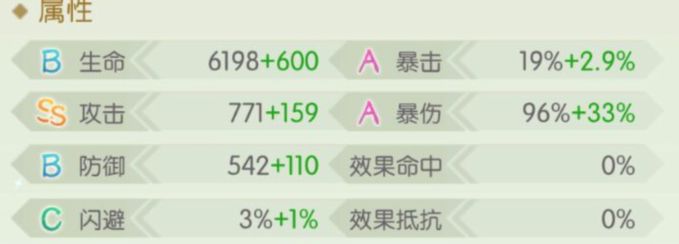
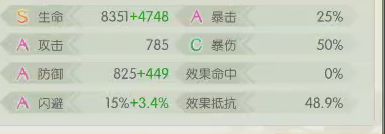
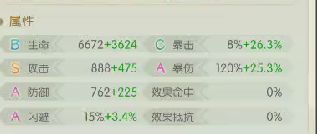
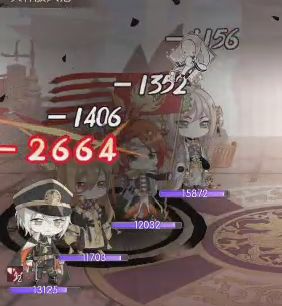
8个数据暴击和闪避不要还剩6个

实际伤害敌方防御伤害率（实际伤害/理论伤害）

1474 832 0.62262397567

1381 832 0.58334037341

1530 652 0.64627861789

1156 1274 0.48829940019

1352 987 0.57109064797

1406 912 0.59390048154

设x为防御力，y为伤害率

获得6个坐标

832,0.623

832,0.583

652,0.646

1274,0.488

987,0.571

921,0.594

然后我们通过鸡丝的测试确定坐标点

0,1

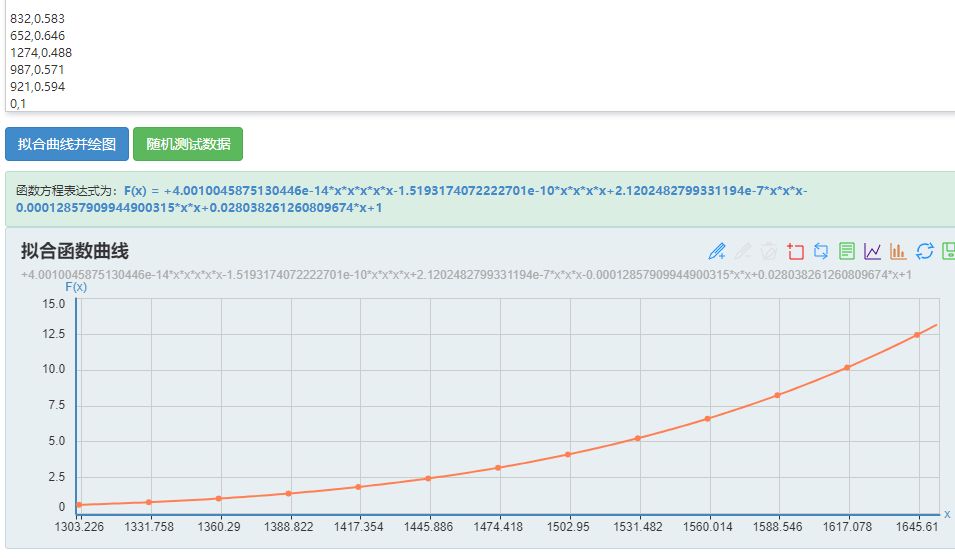
获得函数大致形状

防御越高，防御与伤害率曲率越大。也可以反过来说

防御减低率越多，防御减低的收益率越高。

上面的函数形状可以理解成

F(x)= 1 -X/(X+Y)

即

1-防御/（防御+X）

防御系数与攻击力：

有的游戏是每点防御对应不同的伤害率的，有的却是和攻击力挂钩的。这里就需要验证一下X是否和攻击力相关。

92级四花一品锅有膳具无暴击无加成珍馐57

攻击*倍率=理论伤害

1246*190%=2367.4

实际伤害伤害率（实际伤害/理论伤害）

1606 0.67838134662

1602 0.67669172932

1643 0.69401030666

1564 0.66064036495

92级四花一品锅无膳具无暴击无加成珍馐57

攻击*倍率=理论伤害

924*190%=1755.6

实际伤害伤害率（实际伤害/理论伤害）

1052 0.44436935034

2327(暴击) 0.60248762402

1059 0.60321257689

1014 0.57758031442

可以看到伤害率随攻击力下降而下降。

即认为

伤害率= 1-防御/（防御+X）的X与攻击力相关

假定

伤害率= 1-防御/（防御+攻击）

即假定公式为

攻击*(1+攻击加成)*倍率*（1+暴伤）*（1-防御/（防御+攻击））*（1-（穿透+防御降低））*(1±10%)=实际伤害

化简一下

攻击*(1+攻击加成)*倍率*（1+暴伤）*（攻击/（防御+攻击））*(1-减防-穿透)*(1±10%)=实际伤害

如果 (1-减防-穿透)=0，（攻击/（防御+攻击））*(1-减防-穿透)=1

验证：

带入之前测试函数图所用的数据

实际伤害防御力

1474 832

1381 832

1530 652

1156 1274

1352 987

1406 912

理论伤害2,367.4 *1246/（1246+防御））

1419.529

1554.152

1170.547

1320.994

1366.905

实际伤害都在理论伤害伤害波动的（1±10%)之内。

攻击加成与伤害率：

已经知道攻击力与减伤率挂钩，那么攻击力加成是否也会影响到减伤率呢？

还是这个一品锅二技能进行测试

无暴击，无攻击力加成

无暴击，有攻击力加成

无攻击力加成理论伤害

1246*1.9=2,367.4

有攻击力加成理论伤害

1246*1.9*1.25=2,959.25

无攻击力加成

防御力伤害率

1620 0.68429500718

1654 0.69865675425

1666 0.70372560615

1475 0.62304637999

有攻击力加成

防御力伤害率

2000 0.67584692067

2067 0.69848779251

2265 0.76539663766

1979 0.66875052801

减伤率没有明显变化，即测试中攻击加成不影响防御系数。

即伤害机制公式：

攻击*(1+攻击加成)*倍率*（1+暴伤）*（攻击/（防御*（1+防御加成）+攻击））*(1-减防-穿透)*(1±10%)=实际伤害

中的

攻击/（防御*（1+防御加成）+攻击)

不会计算攻击加成，即攻击加成没有额外的二次收益。

防御加成与穿透减低防御：

先前测试的(1-减防-穿透)与防御加成之间的关系仍然不明确，所以补充测试一下。

一花鸡丝测试水月阁8

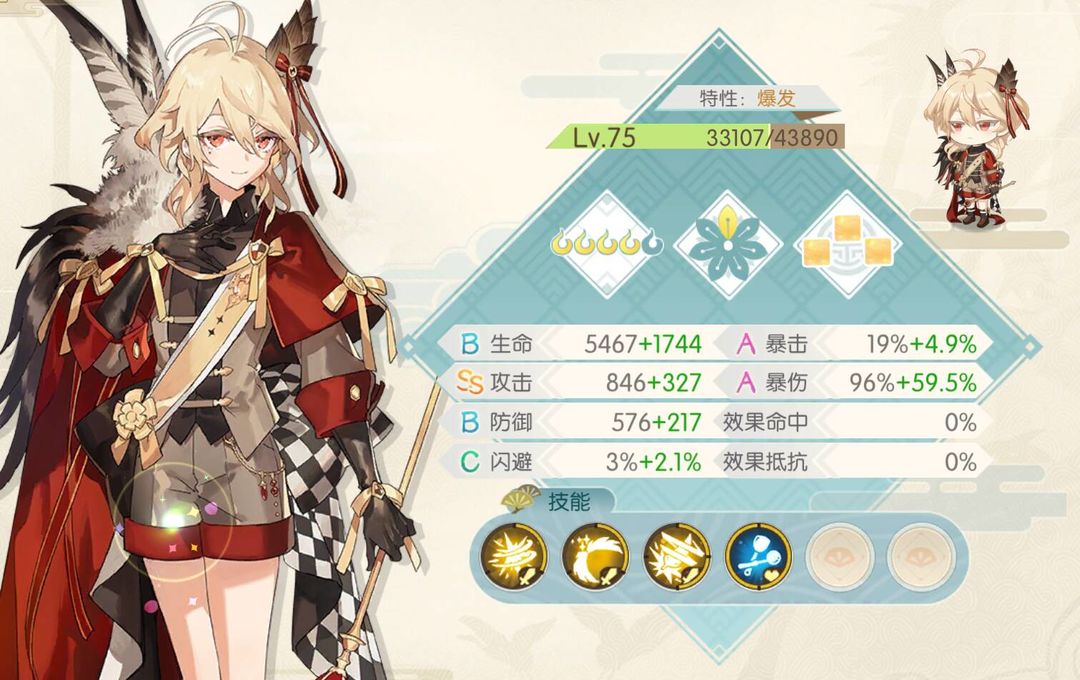
攻击*倍率=1173*395%=4,633.35

防御加成，无暴击 1333

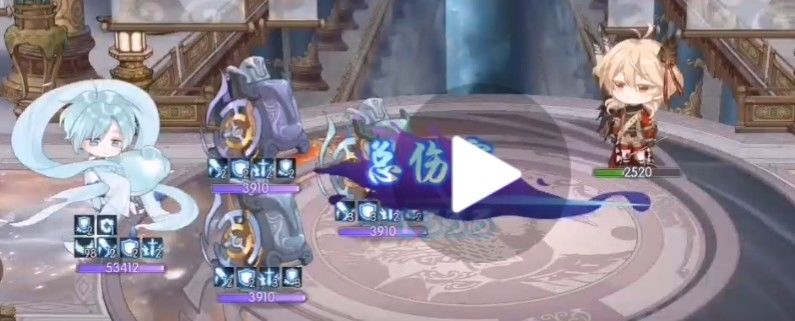
防御加成，降低防御，无暴击 1762

无加成，无暴击 2022

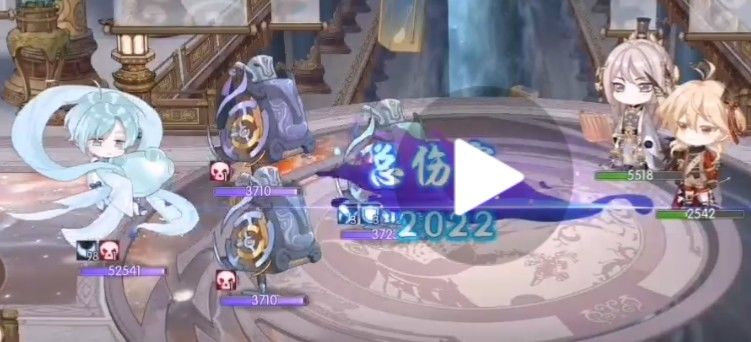
防御加成，穿透，无暴击 3928

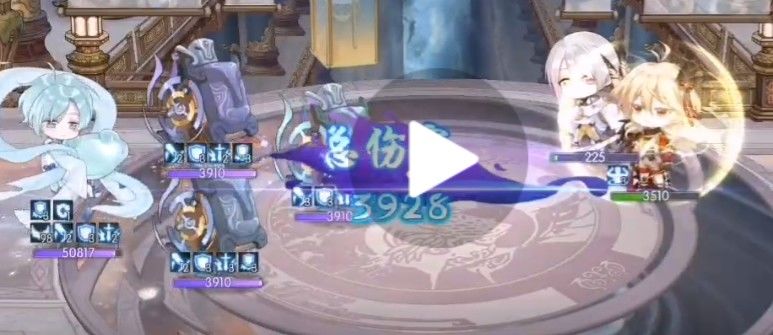
防御加成，降低防御，穿透，无暴击 3917

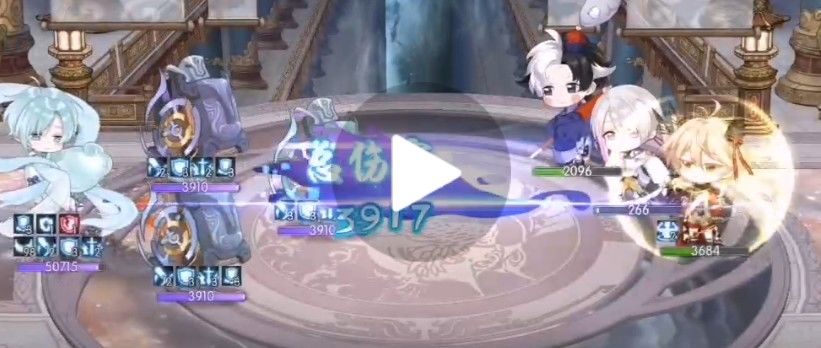
可以看到穿透与降低防御的上线仍然保持在100%，并没有因为防御加成而增加其上线。

即防御加成优先级高于穿透与减低防御。

另外看到防御加成，减低防御是低于无加成的。如果防御加成与降低防御是乘算则170%*40%=68%，低于100%防御。防御越高伤害越低，与实际伤害不符，逻辑错误。

则防御加成-减低防御为加算。

原先公式由：攻击*(1+攻击加成)*倍率*（1+暴伤）*（攻击/（防御*（1+防御加成）+攻击））*(1-减防-穿透)*(1±10%)=实际伤害

更改为：攻击*(1+攻击加成)*倍率*（1+暴伤）*（攻击/（防御*（1+防御加成-减防-穿透）+攻击））*(1±10%)=实际伤害

结论：

伤害机制公式

攻击*(1+攻击加成)*倍率*（1+暴伤）*（攻击/（防御*（1+防御加成-减防-穿透）+攻击））*(1±10%)=实际伤害

在本次测试中成立。

公式化简：

（攻击^2）* 倍率 / （防御+攻击力） = 伤害

食物语

7.9

页面已失效

前往论坛