终极“图论”，教你3000+迷宫思路

“图论”指的不是数学上的图论，仅仅表明本贴是讨论自建迷宫的构建思路。本贴不讨论正常游戏中如何实现，因为楼主目前还没过30关，还在看其他大佬贴子的学习过程中。但话说回来，一个没超过30关的玩家为何敢说这是“终极”呢？因为接下来的内容在一定程度上可以数学证明。但是不建议除专业人员、数学爱好者以及有奥数基础的玩家深入考虑。我们作为普通玩家，能理解就行。如果非要考虑（肯定有人不听劝），建议从图论角度入手。

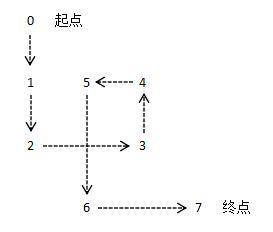
将起点，经过的6个点和终点依次记为点0~7（如图）。迷宫长度就是从起点（点0）出发，依次经过点1~6，最终到达终点（点7）的路径总长度。

假设点0至1，1至2，…，6至7，每次都进入一个“泛迷宫”（区别于后面提到的“真迷宫”和“终极迷宫”）。显然，任意一次游戏的任意一个时间，有且仅有7个泛迷宫。而7个泛迷宫的长度之和就是迷宫的总长度。又由于地图限制，泛迷宫的最大长度是有限制的。于是，有个简单的想法：如果7个泛迷宫都是最大长度，那迷宫总长度也将达到最大值。显然，这是不可能的。理由如下：假设点0至1的泛迷宫达到最大长度，那它必定会经过点2，那么点1至2的泛迷宫就达不到最大长度。

虽然以上想法不能实现，但却给出了提示，如果点0至1的路径尽可能长，点0至2的路径尽可能短，那么点0至1，点1至2这两个泛迷宫的长度之和将达到最大值。

定义“真迷宫”如下：

有3个关于真迷宫的重要结论：

①真迷宫的路径长度大于等于1。

②每个泛迷宫都可以看作由若干个不重合的真迷宫组成。

③组成全部泛迷宫的所有不重合真迷宫的长度之和不超过迷宫的最大长度。

④每个真迷宫最多只能使用/经过7次。

根据以上4个结论，可以建立模型如下：

已知条件: 地图上有若干个不重合的真迷宫, 依路径长度由长至短, 依次记为M1,M2,...,Mn, 其长度分别为L1≥L2≥...≥Ln≥1. 另记每个真迷宫分别使用A1,A2,...,An次.

限制条件: ①以上真迷宫总长度不超过迷宫长度最大值, 即L1+L2+…+Ln ≤ 最大长度;

②每个真迷宫最多只能使用7次, 即A1,A2,...,An ≤ 7.

目标: 构建真迷宫组合(M1,M2,...,Mn), 使得路径总长度S达到最大值, 其中S = A1·L1+A2·L2+...+An·Ln.

模型构建了，问题也是必然有解的，但不推荐除专业人士、数学爱好者以外的玩家尝试。还是那句话，我们作为玩家，只要能借着模型理解问题就够了。接下来将在模型的基础上，讨论怎么构筑迷宫。

这里将我们目标构建的迷宫称为“终极迷宫”。

通过模型，很快能发现构筑终极迷宫的两个条件：（1）A1 = 7，（2）L1 尽可能接近最大长度。

（1）A1 = 7

A1 = 7 意味着每个泛迷宫都必须包含迷宫M1。又真迷宫只有一个入口和一个出口，所以，从点0至1必须通过迷宫M1，可推出，点0和点1分属迷宫M1的入口侧和出口侧。类似地，可以推出，点0、2、4、6属于入口侧，点1、3、5、7属于出口侧（出、入口仅为方便记忆）。

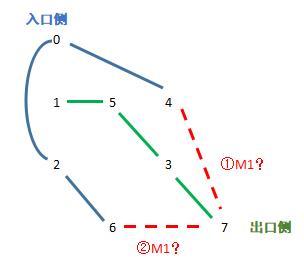
（2）L1 尽可能接近最大长度

L1 尽可能接近最大长度意味着L2+…+Ln要尽可能小。因此，入口侧和出口侧各点之间的连线要近可能短。考虑各点在棋盘上的位置，可以发现出口侧最短的连接方式是 1~5~3~7。在此基础上，入口侧的最短连接方式是 6~2~0~4。

剩下的问题就是迷宫M1的入口在入口侧的哪个点和出口在出口侧的哪个点？这一选择的方向将决定最终模型，个人推荐依据以下两个条件选择：首先，必须是端点的；其次，优先考虑起点或终点。因此，迷宫M1就只剩2种方案，①连接4~7，②连接6~7。如果再观察下，会发现方案①比方案②多经过一次0~2段，所以，一般情况下推荐将迷宫M1的出入口定为点4和7。那么会不会有特殊情况呢？暂时没发现这种可能。

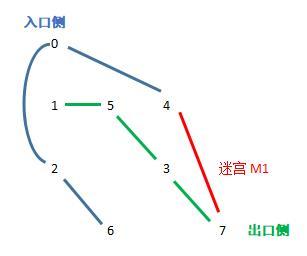
以上，就是终极迷宫的简化模型（不排除这不是最终极的模型）。按照这一模型，尽量将所有空间都用在迷宫M1上，终极迷宫总长度的下限都是3000+。稍微花点心思就能达到3200+。目前楼主在自建迷宫里长度达到3323，如果有一天不愿肝了，就把图放出来。（后续还有些内容，也等肝完了加上）