(转)三门问题
修改于2019/06/20270 浏览综合
三门问题在数学界又被称为蒙特霍尔问题(Monty Hall problem),该问题起源于美国一个名为“Let's Make a Deal”的电视节目,在这个游戏节目中,参赛选手会面对三扇门,其中有一扇门是跑车,其与两扇门羊,如果参赛者选择了后面是跑车的门,就可以把跑车带走了。游戏开始时,主持人让选手先选择一扇门,因为主持人知道门后面是什么,并会在剩余的两扇门中选择一扇背后为羊的门,然后询问参赛者是否转换那扇没有你开启的门。大部分参赛者认为这时关闭的两扇门中奖的概率是一样的,即都是1/2,通常他们不会改变他们第一次的选择。
正确回答这个问题的人是玛莉莲·莎凡小姐(Marilyn vos Sa-vant),如果你们去查一下这位小姐的名字,你们就会知道,她就是吉尼斯世界纪录中世界最高智商的纪录保持者,她的智商为228,或许是考虑到她的智商,有一个Craig F. Whitaker(我想这是个人名)向她问出了这个问题:
“假设你正在参加一个游戏节目,你被要求在三扇门中选择一扇:其中一扇后面有一辆车;其余两扇后面则是山羊。你选择了一道门,假设是一号门,然后知道门后面有什么的主持人,开启了另一扇后面有山羊的门,假设是三号门。他然后问你:“你想选择二号门吗?”转换你的选择对你来说是一种优势吗?”
玛莉莲在华盛顿邮报的刊物《展示》(《Parade Magazine》)中自己的专栏“Ask Marilyn”进行了回答,她认为:这个游戏当中,参赛者换门后的中奖概率是不换的两倍。
“是的,你应该换门。一号门只有1/3的机会赢车,而二号门有2/3的机会。这里有一个看清问题的好办法: 假定有一百万扇门,而你选择了一号门。主持人知道车的所在。他跳过藏车门,打开除777777号之外的所有门。你肯定会急不可耐地换门,对不对?”
这个答案立刻引起大家的争议,大约有10000封信件寄到了杂志编辑部,玛莉莲的超高智商没有使人们信服她的答案,来信中的大约十分之一是来自数学或科学研究机构,发信人有博士头衔。
“我们系里的同事都对你的回答有一个正当的,自认合理的嘲笑。”来自Mary Jane Still,Palm Beach Junior College的教授。
“你错了!让我解释一下:如果被打开的门后什么都没有,信息改变了剩余的两种选择的概率,哪一种都只能是1/2,作为一个职业数学家,我对公众如此缺乏数学技能感到非常关切,请你承认错误,并且将来在回答问题时谨慎一些。”来自Rober Sachs,弗吉尼亚州Fairfax郡的George Mason大学的数学教授。
有无数类似的信件,这里不能在一一陈述,但可以给你们一个发信人名单,这里全部是拥有博士头衔的人:
Barry Pasternack (加州教授协会)、Frank Rose (Univ. of Michigan)、James Rauff (Millikin University)、Charles Reid (Univ. of Florida)、W. Robert Smith (Georgia State Univ)、E. Ray Bobo (Georgetown Univ)、Kent Ford (Dickinson State U.)、Glenn Galkins (Western State College)、Everrtt Harman (U.S. Army Research Institute)……
还有大批报纸专栏作家也加入了声讨玛莉莲的行列,他们大都借此表达了对这个国家国民数学上的无能的悲痛。在这种情况下,玛莉莲向全国的读者求救,请中小学读者在用扑克牌模拟试验,得到了广泛的响应,有数万名学生进行了模拟试验。一个星期后,实验结果从全国各地飞来,是2/3和1/3。随后,麻省理工学院的数学家和新墨西哥州的阿拉莫斯国家实验室的程序员都宣布,他们用计算机进行模拟实验的结果,支持了玛莉莲的答案。

不久,玛莉莲的专栏登出了来自Sachs博士(之前的那位Rober Sachs)的道歉信,他也在公开场合承认了错误:
“我写给她另一封信,告诉她在我不那么尴尬后,我现在道歉并承认错误,作为惩罚我发誓回复所有写信批评我的人,这是个专业领域的感觉很糟的尴尬。”
而Sachs博士的专业上的许多同行理解他的这一处境,Persi Diaconis,前专业魔术师,专攻概率和统计的现任哈佛大学教授说:
“在这个问题上犯错不需要觉得尴尬,我不记得我对这个问题的第一反应是什么,因为我已经知道它好多年了,我是写论文研究这个问题的几个人之一。但我确实知道在类似问题上,我的第一反应一次次地出错,我们的大脑还不能很好地分析概率问题, 所以会犯错不奇怪。”
玛莉莲本人说:
“我并不介意他们是否提出反对意见,因为这意味着他们认真地理解了这个问题,但是他们没有从最初错误印象中前进一步,这使我很沮丧。”
但是玛莉莲承认她在叙述上有一点含糊不清的地方,即主持人是有意识地打开了一扇门,还是随机打开的,这里实际上是前者。于是,Mueser和Granberg两人提出了一种不含糊的陈述:
1、参赛者在三扇门中挑选一扇。他并不知道内里有甚么。
2、主持人知道每扇门后面有什么。
3、主持人必须开启剩下的其中一扇门,并且必须提供换门的机会。
4、主持人永远都会挑一扇有山羊的门。
5、如果参赛者挑了一扇有山羊的门,主持人必须挑另一扇有山羊的门。
6、如果参赛者挑了一扇有汽车的门,主持人随机在另外两扇门中挑一扇有山羊的门。
7、参赛者会被问是否保持他的原来选择,还是转而选择剩下的那一道门。
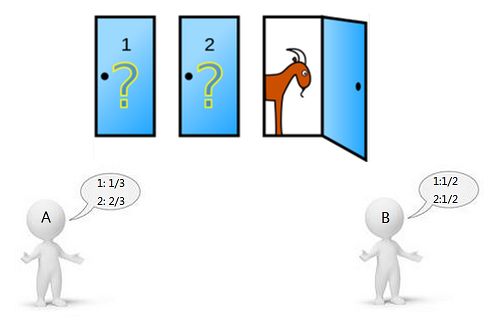
转换选择可以增加参赛者的机会吗?
其实这个问题只有三种情况:
1.参赛者选择了山羊门1,则主持人会选择山羊门2,则换门成功;
2.参赛者选择山羊门2,主持人选择山羊门1,则换门成功;
3.参赛者选择了背后为车的门,主持人选择了任意一扇山羊门,则换门失败。
按照以上的情况来看,选择换门,成功概率为2/3.
事实上,早在玛莉莲事件之前(玛莉莲事件是发生在1990年),1975年,一个叫Steve Selvin的人就向《American Statistician》杂志询问了这个问题,并且首次称这个问题为蒙特霍尔问题。而在更早的1959年,马丁·葛登能(Martin Gardner)就提出了一个相同的问题“三囚犯问题”,把它称为“一个非常容易错的小问题”,并且说:“专家在概率论中,比在其它的数学分支中更容易犯错。”至于这个问题最早的提出者,可能是约瑟夫·贝特朗(Joseph Bertrand),他在自己的书《Calcul des probabilités》中提到了这个问题,并称之为贝特朗箱子悖论(Bertrand's Box Paradox)
---------------------
作者:BigDreamer_
来源:CSDN
版权声明:本文为博主原创文章,转载请附上博文链接!

