小灰的数独迷你课堂第十六讲——链的进阶知识
修改于2021/05/092768 浏览攻略
前言:这一讲可能部分玩家看不明白,或者不会用。这也正常,不必强求。如果你没有看过我的第八讲或是没有链的基础,后面的内容估计可以不用看了。。。建议可以复习一下,我默认大家已经有了一定基础。前面先介绍一些我之前没介绍的小技巧,后面才是重点——AIC & Nice Loop。
首先你必须明白链的概念,强链是两者必成立至少一个,弱链是两者至少不成立一个。
之前我简单介绍了几种双强链,他们都是单数链,下面我们先介绍一个简单的异数链。
1.远程数对(Remote Pair)

远程数对是最简单的异数链,链组成的格全部是同一数对。不需要管格与格是否是强链还是弱链,因为每个格中的两个候选数本身就构成强链关系。如果用链解释就是强弱链交替,两强端点消除共同作用格。
如果用假设解释也很简单,假设r2c7是5,r2c2就是4,r3c1就是5,r6c1就必须是4,r6c7一定不是5.(因为r2c7是5,处在同一行)同理假设r2c7是4,最后r6c7也一定不是5。
这种例子我觉得这个APP里是有的。(我解释链的基础那一讲就是)
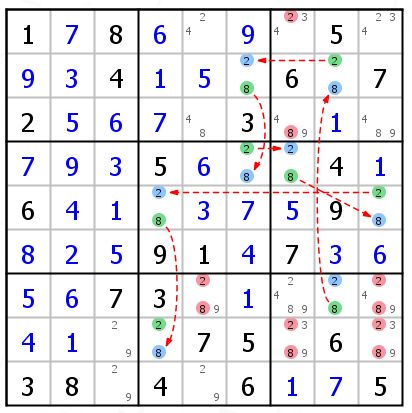
给个复杂一些的例子,自己分析。
2. X-Chain
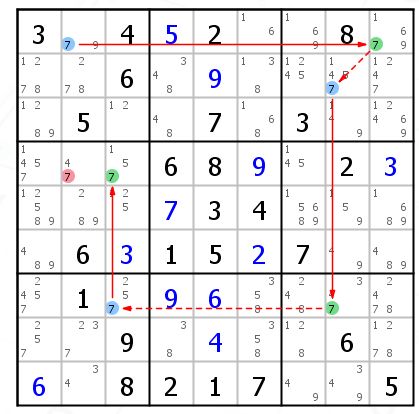
X-Chain就是单数链,只不过我之前介绍的双强链那些长度是4。这个是加长版,长度不限,就看你能找不找得到。图上已经非常清晰的用实线表示强链,虚线表示弱链画出这条链了。没什么说的,想用假设去解释也可以自行推导。
3. XY-Chain
XY-Chain可以认为是XY-Wing的扩展,原理是和XY-Wing相同的,若双值格的数目变多,但还是可以通过中间的联系把双值格前后链接起来,则首尾两个双值格中共有的候选数互为强关系,可以删除共同作用格中的该候选数。
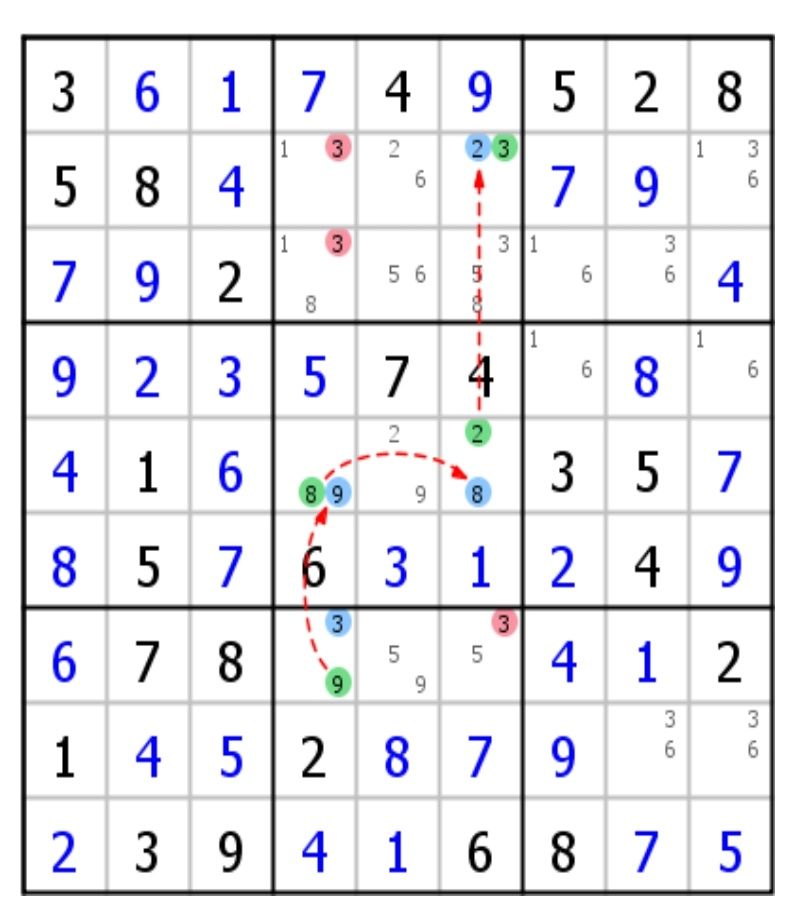
这里强链就是双值格两候选数之间相连,和前面例子一样。
R7C4{3}==R7C4{9}--R5C4{9}==R5C4{8}--R5C6{8}==R5C6{2}--R2C6{2}==R2C6{3}
(这里例子只涉及四格,和X-Chain一样,想多长都可以)
XY-Chain的找法和XY-Wing基本一样,都是先看双值格,只要能连下去,就一直连着,出现和第一个格子一样的候选数了,看看共同作用格是哪些,去删除掉这个候选数。
4. AIC(交替推理链,Alternate Inference Chain)
在链的基本理论中,已经说了链的强弱交替理论,AIC 简单来说就是一个强弱交替的链,区别于简单异数链里面的结构,我们这篇文章会给出强弱交替链的灵活运用,让大家更容易解题。
根据链首尾的候选数是否相同,把 AIC 分为两种类型。
4.1 Alternate Inference Chain Type 1
首尾候选数相同,删除共同作用格的候选数
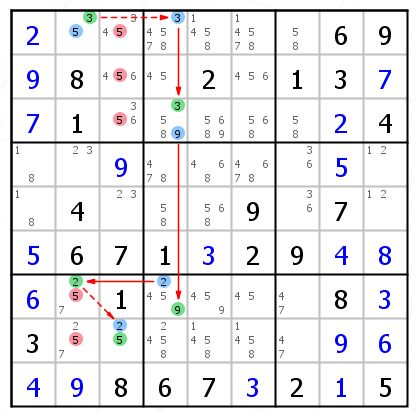
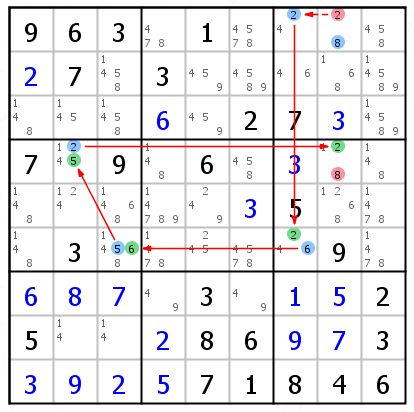
这个AIC是这样的:R1C2{5}==R1C2{3}--R1C4{3}==R3C4{3}--R3C4{9}==R7C4{9}--R7C4{2}==R7C2{2}--R8C3{2}==R8C3{5},得到结论 R1C2{5}==R8C3{5}
可以删掉他们两个的共同作用格,就是图中红色的5。
图中的格中均标记颜色(蓝绿)均是构成链关系的,只是距离太近就不标出来了,上面符号已经给出完整的链了。(其实就是一条长的异数链)
4.2 Alternate Inference Chain Type 2
当首尾候选数不一样的时候,我们能够做什么呢?来看下 AIC2 的例子

具体的链我就不写了,最终的结论是R6C2{4}==R6C4{8}
为什么能够删掉R6C2的8和R6C4的4呢?
因为两者构成强关系,所以R6C2{4}和R6C4{8}一定会成立一个,如果R6C2 = 4,那么红色的4和8 可以删掉对吧,如果R6C4 = 8,红色的4和8一样也可以删掉吧。
所以红色的4和8一定是可以消除的。
这个例子最后得到 R1C8{8}==R4C8{2},然后删掉了红色圈中的候选数(仿照上面自己假设一下)
看了两个例子你知道怎么用AIC删除候选数了么?
AIC2的结论:互为强关系的两端候选数可以将对方格内的自己进行删除(有个前提,两端候选数要在同一个行列宫,不然无法删除数字)
怎么找???不知道,没有什么技巧可言。。。就是用多了就熟了,我也无法每次都准确找到。(特别是那种没有候选数高亮的APP,更不好观察,如果是极高难度,候选数很多就需要使用这种技巧的话。。。)
5. Nice Loop(就是异数环)
根据环中链的强弱交替不同,分为两种结构 Continuous Nice Loops (AIC Loops) 和 Discontinuous Nice Loop。
5.1连续环Continuous Nice Loops (AIC Loops)
当一个环中链一直是强弱交替的,它就是一个连续环,断开环中任意一个弱链,这个弱链的两端都是强关系,可以对共同作用格进行删除。
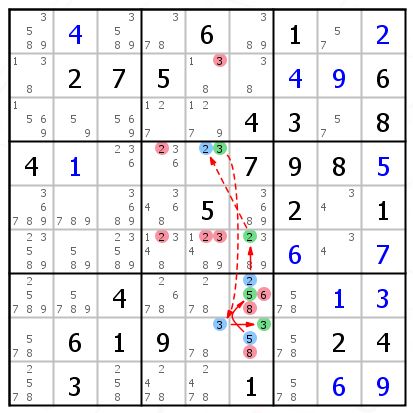
R5C5{2}==R5C5{3}--R8C5{3}==R8C6{3}--R8C6{5}==R7C6{5}--R7C6{2}==R6C6{2}--R5C5{2}
因为是一个连续环,所以中间任意一个弱链都可以断开得到一个强关系
R5C5{3}==R8C5{3},删掉了R2C5的3和R6C5的3。
R8C6{3}==R8C6{5},这个强链出现在同一个单元格,那么单元格中其他的候选数都可以删除,删掉了R8C6的8。
R7C6{5}==R7C6{2},也是单元格强链,删掉了R7C6中的6和8。
R6C6{2}==R5C5{2},删掉了B5中的其他2。
其实你完全可以把它拆开,拆成一推短链。道理一样。
连续环怎么找,有这么几个规则:
1、若某单元格通过两条强链与其他单元格联结,该单元格联结两条强链的候选数不同;
2、若某单元格通过两条弱链与其他单元格联结,该单元格必为双值格且两个候选数分别联结一条弱链;
3、若某单元格通过一条强链和一条弱链与其他单元格联结,该单元格内联结这两条链的候选数相同。
这几个规则随便看一看就好,我觉得还是多做题更容易理解。。。
5.2 不连续环Discontinuous Nice Loop
当环中不满足链强弱交替的时候,就出现了不连续环,但这个不连续不能是 A==B--C--D==A 这种,只能有一个节点是强进强出或者弱进若出(==A== 或者 --A--),其他节点必须强弱交替,这种结构在链的基本理论中已经说过,==A== 这种A一定为真,--A--这种A 一定为假。(前面我已经说过了)
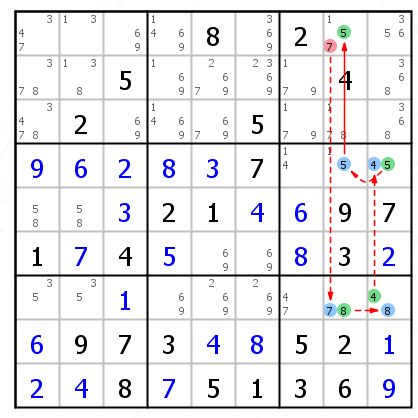
R1C8{7} 弱链开始,最后弱链结束,所以7可以删除。(弱进弱出)
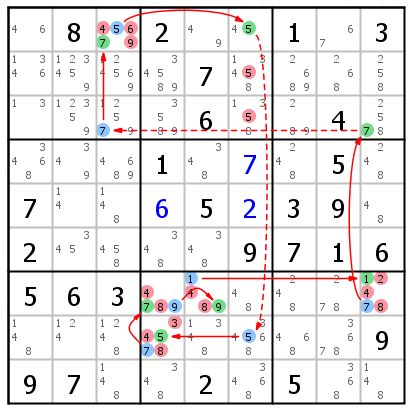
R8C2{4} 强链开始,强链结束,所以R8C2 = 4。
6. Grouped Nice Loop/AIC
Group的概念我之前就使用过,比如空矩形等等。这里再说明一次,Group并不等同区块,但是我经常简单解释说是看作区块。区块是候选数X必须出现在里面,相当于是所有某范围内含有候选数X的集合。而Group是在一定情况下,可以看为区块,主要是用于链连接非单一格使用,但是候选数X最后不一定出现在Group。我因为之前没有介绍Group的含义,所以用区块来解释。
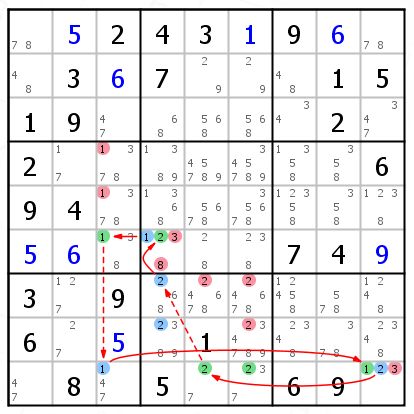
这一个是通过Group形成的连续环
R78C4{2} 是一个 Group 和 R6C4{2} 是强关系
R9C56{2} 是一个 Group 和 R9C9{2} 是强关系
这里最后解释一下,我前面解释使用的区块概念其实其中一些应该是Group。比如R78C4{2},我之前会直接说2的区块。不严谨但道理类似。这里R78C4{2}不是区块,我说过2的区块是候选数2必须出现在这个范围内。观察b8,最后如果2出现在R9C56也成立。但是为什么用R78C4{2}的概念呢?这里是作为链连接的对象。观察C4,候选数2仅出现在C4R678,如果是严格意义上的2的区块,应该是R678C4{2}.这里是Group R78C4{2}。道理很简单,2一定出现在R678C4中一个,我随便拆成两组,他们都是强链关系。(一定会成立一个)我现在这样连是为了这个链成立。链的使用非常灵活,连宫连Group连区块都可以。
上面例子自己理解吧。。。如果不能独立理解,是不可能会用的。
通过Group的引入,上面讲的那些技巧就都升级了,全部可以使用Group,包括之前那些各种技巧,其实一部分就是变形。
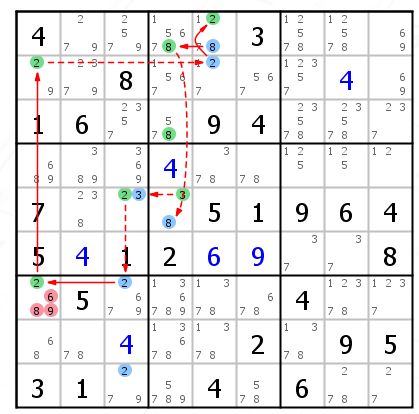
这个例子是一个不连续环
R79C3{2} 是一个Group和R7C1{2}是强关系,最后得到 R7C1{2} 强进强出,R7C1 = 2。
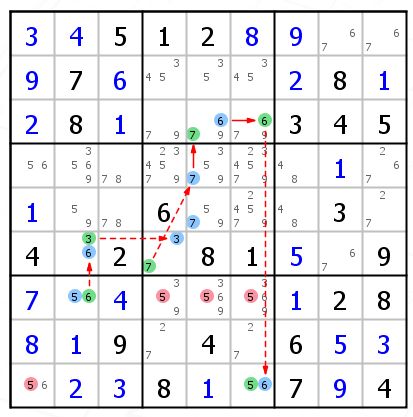
这个是个 AIC1 的例子
Group是R45C5{7}和R3C5{7}是强关系。
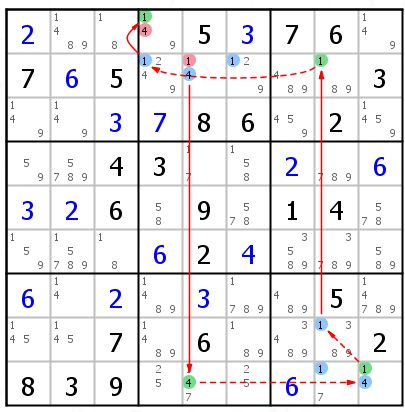
这个是AIC2的例子
有两组Group
R2C456{1}和R1C4{1}是强关系
R89C8{1}和R9C9{1}是强关系
你应该看到了,就算我再懒,我也把所有Group和XXX是强关系写出来了。找Group的时候,一定要找强关系。你必须明确你这个Group和什么强关系,因为强弱链删除候选数依据必须是两强端共同作用的区域,如果这个链的一端是Group,你必须知道,它的作用区域是什么,不然你会删错候选数。
这一讲难度,道理很简单,用起来就。。。
习题就一个吧。。。

找到连续环。
答案见回复,附上总集篇链接。


