小灰的数独迷你课堂第十五讲——着色法(Coloring)
修改于2021/05/081708 浏览攻略
前言:这个方法非常好玩,特别适合学前儿童。不过其实没啥必要,会了强弱链,完全可以替代。该方法本质我认为就是链,只是用更加直观的方式(涂色)。不过很遗憾,大部分APP并不支持直接使用该技巧,所以该方法几乎用不到。如果你愿意交小朋友数独,我觉得这个技巧非常棒。你可以考虑在纸或截图的方式使用该技巧。由于我没有找到任何关于此方法的介绍。。。所以我硬着头皮来了。
1.简单着色(Simple Colors)
“简单颜色”仅使用两种不同的颜色。从共轭对(就是只有两个候选数)的一个单元格开始,通过着色,直到没有可继续画的格。 之后,我们可能发现两个可能矛盾之一:
(1)如果一个无色单元格在相反颜色的单元格共同作用区域(Color Trap):由于具有相同颜色的单元格全部为真或全部为假,因此两个有色单元格之一必须为真,所以无色单元格的该候选数可以删除。(就是类似一条链,两个端点共同作用区可以删数)
(2)具有相同颜色的两个单元格在同行同列同宫(Color Wrap):具有相同颜色的单元格全部为真或全部为假。 全部为真是不可能的(同一行列宫中将出现两次相同的数字),因此它们都必须为假。
觉得不好理解?看粒子。

我先演示如何得到这个图吧。。。

首先我们随便选一个起点(该方法我这里只介绍最基本的,一般来说选比较简单的仅含有两个候选数的格,而且该方法是针对单一候选数使用的,就是说这个例子你只需要关注候选数3)然后找到和它同行同列同宫且该行列宫仅出现两次3的格(其实就是强链),用另一个颜色标记。

再以该格为起点接着找满足之前关系的格(R7C5),注意两个颜色必须交替使用(就是强弱交替)直到你找不到了。

就是这样。(注意你只看候选数3就行,完全不需要管这个格有几个候选数,只有起点是两个候选数就行)
这个例子就只有前面说的第一种情况(Color Trap),红色标记的候选数都可以删掉。他们都是在行列宫存在两种颜色格的位置。(比如R8C1,同列有深颜色的格,同宫行有浅颜色的格)你仔细想想前面的链的知识,就是强弱链连接,两个强端点共同作用的区域可以删数。只是这种非常直观,比你去记链更容易观察。

这个例子中我们把其他不属于这种关系但包含候选数8的格用绿色标记来表示区别。我就不从头画了。这里属于第二种情况(Color Wrap),红色候选数可以删掉。这些格都是该行列宫有两个以上同种颜色的格。(我们知道因为这些格都是同真同假的关系,仔细想想,他们如果都是强链连接,第一个格是8,第二个就不能是8,第三个就必须是8,所以13是同真同假,就是相同颜色的格。而同行列宫出现两个这样的格,意味着如果都是真,那就有两个8了,所以为了成立就必须都不是8)
我是觉得挺好玩。
2. 多彩着色(Multi Colors)
多彩着色是将多于一种的颜色用于标记。完成着色后,我们再次遇到两种可能导致消除的情况:
(1)如果不同颜色对的两个有色单元位于同一宫(它们形成弱链)。由于他们在同一宫,所以它们不能同时为真(并且所有具有这些颜色的单元格都适用)。但这也意味着,第一个颜色的相反颜色或第二个颜色的相反颜色必须是真的。所以我们可以删掉同行列宫出现至少两个具有这些相反颜色的格的候选数。
(2)具有相同颜色的两个单元格(例如颜色1)同行列宫有具有另一种颜色对相反颜色的单元格。另一对颜色的单元格之一必须为真,这意味着颜色为1的单元格之一必须为假。由于所有具有相同颜色的单元格必须具有关于颜色数字的相同状态,因此所有具有颜色1的单元格都不能包含颜色候选。
不好理解?(原谅我无法很好表达)看例子。
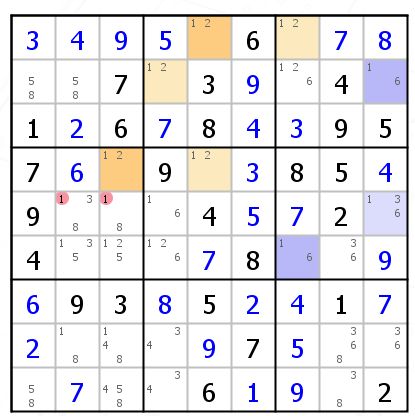
我们前面知道如何用一个颜色画了,那么我们再找一个起点,用不同颜色标记,依然满足相同规则。注意深浅交替标记颜色。得到如图的情况。(你可以自己画,这里的候选数是1)
这种情况满足前面的第一种情况。注意b3,有两个不同颜色的格出现在一个宫。(他们就是弱链关系)记住两者的深浅关系!这个例子中颜色一深一浅的在一个宫(不一定,也可能同深同浅)。由于他们在一宫,所以他们不可能同时成立。那么他们各自对应的另一个颜色(同色不同深浅)必须有一个是真。(比如R1C7和R2C9一定有一个不成立,对应的R1C5和R5C9就必须有一个成立)这样,如果你能找到在同行列宫同时出现一深一浅不同颜色的格,那共同作用的格的候选数就可以删掉。(就是强链关系,可以自己画,比如这个例子中的R4C3和R5C9就是强链关系,共同作用红色标记的格)

图怎么画就不说了。这种就是上面说的第二种情况。(这里候选数是3)我们这里把黄色浅色的叫颜色A1,黄色深色的叫颜色A2,紫色浅色的叫颜色B1,紫色深色的叫颜色B2.
观察颜色A1的格R6C2同行有颜色B1,颜色A1的格R8C6同列有颜色B2。问题来了,同一颜色不同深浅的两格是强链关系,意味着两者必须成立一个。无论哪个成立,他都和颜色A1在同行列宫。说明颜色A1的一个格一定不成立。但是同一颜色同一深浅,逻辑关系上是同真同假的,因此所有颜色A1都不成立。
其实这种方法应该还有一些使用技巧。。。只是我无法找到,因为用的人非常少。。。因为初学者不知道这个技巧,进阶玩家用链就直接完成了,根本用不到(因为花时间,而且很多APP不支持该功能)但是我乐意玩。
习题。。。你怎么做呢???截图自己画?
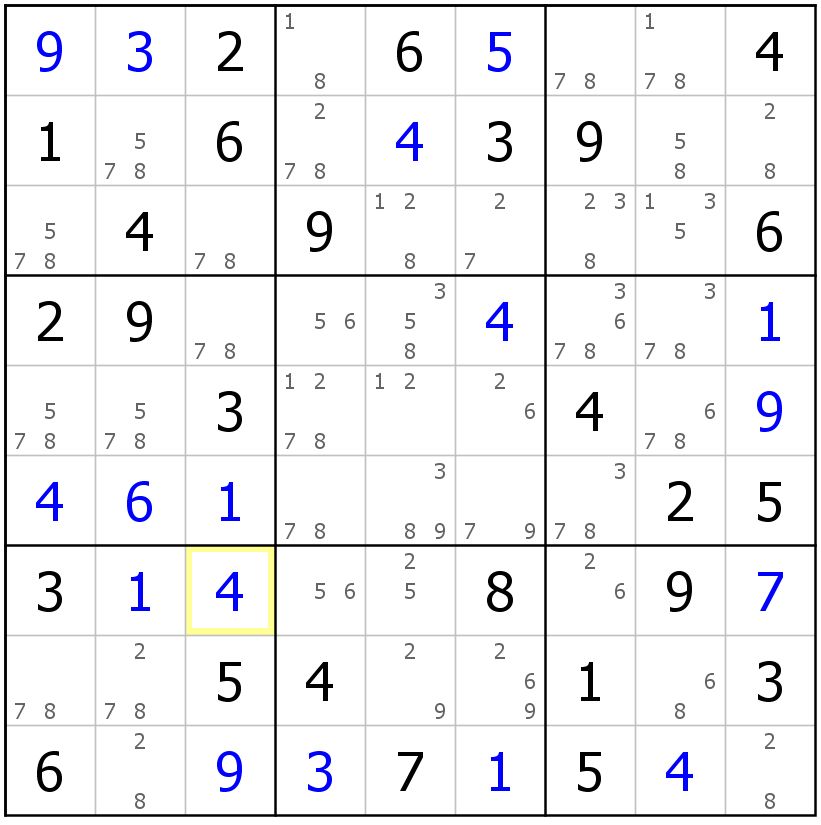
给个习题吧。。。候选数是2
答案见回复,附上总集篇链接。


