双up毒池抽卡指北:以五一周年池为例
精华修改于2020/04/277152 浏览攻略
关于双up毒池的出货期望问题,半天看到了三四套结果,真实离谱。还不如我自己来算算。
太长不看版:
如果不挑,抽中任意一个up的平均次数是50次,吃井率不足0.1%,24抽的白嫖率为28.68%。
如果要挑W/Wendy,抽中特定一个up的平均次数是96次,吃井率是3.61%,24抽的白嫖率为15.50%。
如果全都要,抽中两个up的平均次数是132次,吃井率是7.10%,24抽的白嫖率为6.66%。
(抽卡次数全部向上取整。)
健康游戏,理智氪金。
充钱可能会亏,不氪立赚200%。

目录
1-理论概率:多少抽能中一个up
2-数值模拟:多少抽能中一个up
3-我只想要W/Wendy要多少抽
4-我W和Wendy全都要!
——
1-理论概率:多少抽能中一个up
首先,从最简单的情况讨论起:如果我不在乎抽中W还是Wendy,来个姓VV的就彳亍,那我的抽卡次数期望是多少。
要讨论这个问题,第一,得明白几个基本原理公式:
事件相互独立:P(AB)=P(A)*P(B);
条件概率:P(A丨B)=P(AB)/P(B);
子事件:P(A)=P(A1)+P(A2)+…+P(An)。
对于双up毒池,“出货”其实就可以分成“抽中六星”和“抽中的六星是当期up”两个相互独立的事件,只有两个事件同时满足才会“出货”,因此可以分开算两个事件的概率然后相乘作为“出货”概率。这一逻辑对于计算两个up全都要的情况尤为重要。
第二,依次计算“第n次抽卡能抽中六星”(n=1,2,…,99)[1]的概率,注意“第n次抽卡”意味着前n-1次抽卡都没有出六星。计算出的概率密度分布如下图所示[2],进而算得众所周知的出六星抽卡期望34抽(34.59)。

第三,在70%up率机制下“抽中的六星是当期up”满足70%概率的二项分布。又在300抽的井机制下,我们可以预期一个最非的人出大概8次六星没中up就能吃井(300/34.59=8.67),所以我们只考虑一个人分别在第1-8次出六星的时候中up就能回答“多少抽能中一个up”的问题[3]。
在上述设定下,恰好在第m次出六星的时候中up的概率是P(m)=(1-0.7)^(m-1)*0.7(m<8)。有井机制下恰好在第8次出六星的时候中up的概率是P(m=8)=(1-0.7)^8*100%。
跟34.59的六星抽卡期望联立可得中一个up的抽卡次数期望是
E(任意一up)=49.41[4]

——
2-数值模拟:多少抽能中一个up
接下来用随机抽样的思路模拟出一个10w人的样本[5],每个人中一个up的抽卡次数频数分布如下图所示。

从图中可以看出,50抽左右中一个up的人最多,接近2.5w人,在一定程度上验证了理论推导49.41的结果。
10w样本总体的均值为49.35抽。
采用Bootstrap算法抽样1k次计算的抽卡次数均值也为49.35,90% 的置信区间为【48.75, 49.94】。
然后是大家比较关心的两个问题:
第一,多少人吃井?
10w样本总体中仅有28人吃井(0.028%),若把抽卡次数超过270的人视为“主动吃井”的话(我寻思都抽到这儿了不会不抽剩下30连吧?),吃井人数为也仅为52(0.052%)。
采用Bootstrap算法的吃井率为0.0276%,90% 置信区间为【0.001%, 0.054%】,主动吃井率为0.0529%,90% 置信区间为【0.017%, 0.089%】。吃井率波动相对比较大,但可以肯定的是基本不会超过0.1%。
第二,周年活动能直接白嫖24抽,那多少人能24次白嫖中一个up?
10w样本总体中白嫖到一个up的人数为28699人(28.699%),超过四分之一的人能白嫖一个up,这倒是超乎我的预期。
采用Bootstrap算法的白嫖率为28.683%,90% 的置信区间为【27.978%, 29.389%】。

——
3-我只想要W/Wendy要多少抽
接下来讨论另一种情况:如果我只想要W/Wendy,不想要另一个up,更不想歪其他的六星,那我的抽卡次数期望是多少。
直观来看,跟第一种情况相比,想要特定up的出货率会骤减。同样抽出六星之后,不挑的时候抽中当期up的概率是70%,而想要特定up的时候概率就折半为35%(假设两个up概率平分)。
这里就不再推导理论概率只做数值模拟了,第一种情况的结果也已经证明模拟和理论相当接近了。
仍然模拟出一个10w人的样本,每个人抽中特定up(无论是W还是Wendy)的抽卡次数频数分布如下图所示。

是不是感觉一两百抽才出货地人数肉眼可见的增多了?单吊特定up比不挑剔的出货难度大得多。
10w样本总体的均值为95.48抽。
采用Bootstrap算法计算的抽卡次数均值为95.44抽,90% 的置信区间为【94.24, 96.64】。将近一百抽才能抽中特定up。
仍然是那两个问题:
第一,只抽特定up会有多少人吃井?
10w样本总体中有3611人吃井(3.611%),考虑抽卡次数超过270的“主动吃井”的情况,吃井人数为为5129(5.129%)。
采用Bootstrap算法的吃井率为3.624%,90% 置信区间为【3.324%, 3.923%】,主动吃井率为5.141%,90% 置信区间为【4.785%, 5.497%】。出货难度加大,吃井率增加,波动就小了,可以确定的是这种情况下吃井率在3%到4%之间,主动吃井率在5%左右。
第二,多少人能24次白嫖中一个特定up?
10w样本总体中白嫖到一个up的人数为15504人(15.504%),白嫖比例骤减,但仍然有一至两成。
采用Bootstrap算法的白嫖率也为15.504%,90% 的置信区间为【14.920%, 16.088%】。

——
4-我W和Wendy全都要!
最后讨论最复杂的情况:如果我是W和Wendy全都要的成年人,我的抽卡次数期望是多少。
直观来看,跟前两章情况相比,全都要的出货率又会进一步降低,并且至少要抽出两次六星。
在第一次出六星的时候,全要党不挑,只要是up就行;在拿到一个up之后,则变成只要特定的另一个up。
同样,这里也不推导理论概率而只做数值模拟。
依然模拟出一个10w人的样本[6],每个人抽中两个up的抽卡次数频数分布如下图所示。
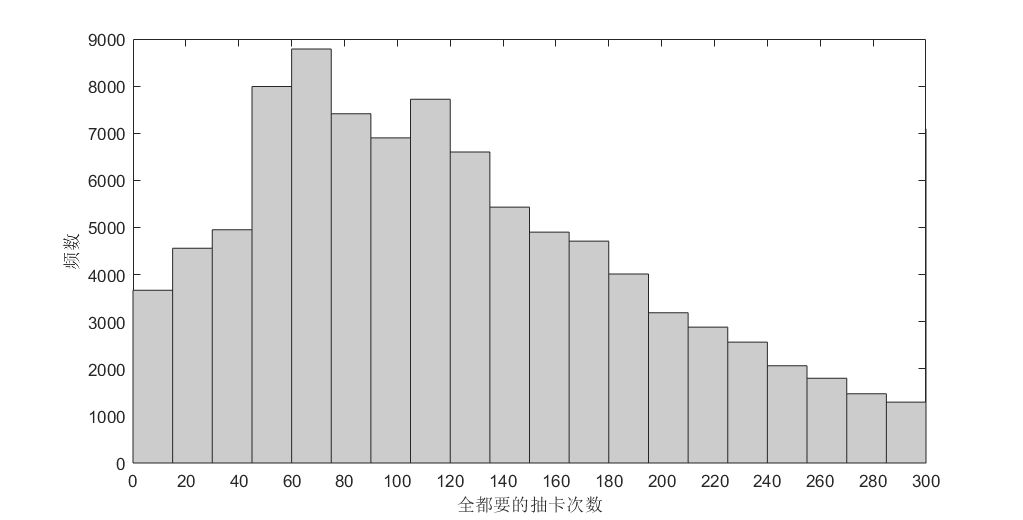
一两百抽才出货的人数又一次肉眼可见地增多了。做全都要的成年人,成本有点大。
10w样本总体的均值为131.53抽。
采用Bootstrap算法计算的抽卡次数均值为131.50抽,90% 的置信区间为【130.186, 132.823】。
依然是那两个问题:
第一,会有多少人吃井?
10w样本总体中有7092人吃井(7.092%),考虑抽卡次数超过270的“主动吃井”的情况,吃井人数为为9855(9.855%)。
采用Bootstrap算法的吃井率为7.100%,90% 置信区间为【6.688%,7.513%】,主动吃井率为9.855%,90% 置信区间为【9.377%, 10.333%】。出货难度继续加大,跟单吊一个特定up相比,吃井率接近翻倍。
第二,多少人能24次白嫖中两个特定up?
10w样本总体中白嫖到一个up的人数为6674人(6.674%),白嫖比例也是进一步削减。
采用Bootstrap算法的白嫖率也为6.657%,90% 的置信区间为【6.249%, 7.065%】。

注:
[1] 需要稍微注意一下的是,在当前的保底机制下其实出六星的理论抽卡上限是99次(50+49)而非盛传的100次。
[2] 为了好看把图画成了连续的折线图,实际上由于抽卡次数只能是整数,概率密度函数应该是非连续的。
[3] 这里做了一个简单粗暴的近似,有很大问题。考虑两种极端情况,一是每次十连都能中六星的天选之人,他吃井需要出的30个六星都不是up,二是一直70抽才能出六星的非洲人,他只用出4个六星就能吃井。两种情况跟假设的8次六星都有很大出入,类似的情况导致这里的估计是有偏的。但要完全考虑这些情况计算无偏估计非常麻烦,我没想到好如何用相对简单的算法来实现,所以只做如此近似计算。
[4] 要注意的是,这个次数期望看起来不多,但这个次数的分布是右偏的,也就是说部分欧洲人用较少次数(一两次十连)出了货把整体期望给拉低了,实际上还有很多一两百抽才出货的人被欧洲人给“平均”了。
[5] 这里我又做了一次近似,从第一张图可以看出抽75+次才出六星的概率近乎于0,不太好模拟,于是我将第75-99次出六星的概率进行加总,均作为第75次出六星看待(实际上,75+次出六星的期望是75.87次,影响不大)。此外,数值模拟可以完美解决理论概率有偏的问题,添加一个if语句判断是否吃井即可。
[6] 对于全都要的情况,仍然假设一个人最多抽300次就能抽齐。也就是说,在前300次中,至少能抽中两个up中的一个,另一个up在最非的时候直接靠井兑换。根据第一种情况的结果,300抽一个up都没有的概率仅为0.0276%,可以忽略不计(讲真,真要这么黑,建议还是弃坑)。




